-
- Indice 'Strumenti Finanziari'
|
|
|
- (Warrant
e Covered Warrant)
Il valore dei
warrants
- a cura di: Salvatore Guarino

-
- Liberamente tratto
da:
- Cedborsa.it -CitibankN.A.
- Tenfore
|
|
- Indice 'Warrant e CW'
|
Il valore intrinseco
Vale a dire
il valore che si otterrebbe esercitando il warrant.
Nel caso di un warrant "call" sarà uguale
a:
|
(livello
del sottostante - strike price) x multiplo |
Così
ad esempio il valore intrinseco di un call warrant con strike
8.000 e multiplo di 1 sul titolo Alfa il cui prezzo di mercato
è di Lit. 10.000, sarà:
|
Lit.(10.000 - 8.000) x 1
= Lit.2.000 |
Nel caso di
un warrant "put" sarà uguale a:
|
(strike
- livello del sottostante) x multiplo |
In questo
caso, dunque, il valore intrinseco di un put warrant con strike
40.000 e multiplo di 1 sull'indice che quota Lit. 35.000 sarà:
|
Lit.(40.000 - 35.000) x
1 = Lit.5.000 |
Moneyness
In base alla
relazione tra strike price e livello del sottostante i warrant
si distinguono in:
- in the money
- Nel caso di
un call warrant i livello del sottostante è superiore
allo strike price. Nel caso di un put avviene il contrario (quindi
il warrant è dotato di un valore intrinseco).
- at the money
- In questo caso
il livello del sottostante è uguale allo strike price
e quindi il valore intrinseco è pari a zero.
Esercitando il warrant l'investitore nn otterrebbe nulla.
- out of the
money
- Nel caso di
un call il livello corrente del sottostante è inferiore
allo strike price. Nel caso di un put avviene il contrario. Anche
in questa ipotesi il warrant ha valore intrinseco nullo poiché
si assume che nessuna opzione possa avere un valore intrinseco
negativo.
Il valore del tempo
Perché
un warrant call con strike 100 (che conferisce il diritto di
acquistare a 100), quando il sottostante vale 110, non vale 10,
ma spesso molto di più?
Perché un warrant call con strike 100 quando il sottostante
vale 80, no vale zero, ma ha comunque un prezzo?
In altri termini, perché un premio di un warrant non
è semplicemente uguale al suo valore intrinseco?
La risposta è che il premio di un warrant ha due componenti:
il valore intrinseco e il valore del tempo.
Il valore del tempo è rappresentato dalla differenza tra
il prezzo del warrant e il suo valore intrinseco. Nel caso di
un warrant call con strike 24.000 ed un prezzo di Lit. 2.500
quando il valore del sottostante è di Lire 25.500, il
valore del tempo è pari a Lire 1000. Cioè pari
alla differenza tra il prezzo del warrant (2500) ed il suo valore
intrinseco (25500 - 24000=1500).
Per meglio
comprendere il concetto di valore nel tempo ci si può
immaginare il warrant come un contenitore; il liquido già
contenuto nel contenitore rappresenta il valore intrinseco del
warrant, la capacità rimanente del contenitore ovvero
la possibilità di riempirlo con ulteriore liquido, rappresenta
il valore del tempo.
Il valore
del tempo può essere definito come il valore che il mercato
attribuisce alle probabilità che il warrant scada in the
money (ovvero
acquisisca più valore intrinseco nel lasso di temo che
intercorre prima della scadenza).
Il valore
tempo assume i valori più elevati quando il warrant è
at-the-money, ossia quando il prezzo di esercizio è
uguale al livello del sottostante: in questo caso, l'incertezza
che il warrant scada "in" o "out of the money"
è maggiore.
Per lo stesso motivo, quando il warrant è molto (deep)
in-the-money e il valore intrinseco del premio è
consistente, la probabilità di essere "in the money"
alla scadenza risulta elevata. La componente valore del tempo,
di conseguenza è debole.
Infine quando il warrant è molto "out of the money"
e il valore intrinseco è nullo, la probabilità
che scada "out of the money" è molto grande:
anche in questo caso il valore tempo è ridotto, anche
se rappresenta l'unica componente del prezzo del warrant.
A questo punto, si può comprendere come per trarre
vantaggio da un warrant sia preferibile venderlo piuttosto che
esercitarlo.
In effetti, l'investitore che decide di vendere il proprio warrant
sul mercato prima della scadenza riceverà il valore intrinseco
sommato al valore tempo residuo, mentre in caso di esercizio
del warrant , riceverà solamente il valore intrinseco
rinunciando completamente al valore tempo.
Possiamo riassumere
quanto detto sul valore tempo nel modo seguente:
Vendita
del warrant --> Premio ricevuto = VI + VT
Esercizio
di un warrant --> Premio ricevuto = VI
dove VI =
Valore Intrinseco e VT = Valore del Tempo
Trading o esercizio
Una volta
stabilito che il prezzo di mercato di un warrant non è
dato solo dal suo valore intrinseco, diviene piuttosto evidente
che per il possessore di un covered warrant, laddove esiste un
mercato secondario di questi strumenti, è sempre preferibile
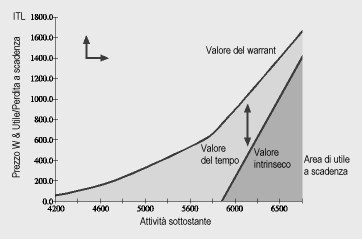
rivendere il warrant piuttosto che esercitarlo. Il grafico
che segue può aiutare a capire il perché
La curva convessa
che appare nel grafico rappresenta la funzione del valore del
warrant e viene confrontata con il profilo di rischio-rendimento
del warrant a scadenza (cioè considerandolo solo l'opportunità,
dell'esercizio). La distanza tra le due curve per un dato livello
del sottostante rappresenta la componente tempo incorporata nel
valore del warrant.
L'esercizio di un covered warrant comporta l'incasso di un importo
in denaro pari al valore intrinseco del warrant in quel momento.
L'esercizio quindi non consente di monetizzare la componente
valore del tempo del warrant, per il semplice fatto che l'esercizio
stesso determina l'estinzione del diritto incorporato nel warrant.
Ritornando alla moneyness dei warrant, possiamo dire che solamente
i warrant in-the-money incorporano nel loro prezzo entrambe le
componenti di valore. Mentre il prezzo dei warrant at-the-money
e out-of-the money incorpora solamente la componente valore del
tempo.
Ne consegue che quanto più un warrant è out-of-the
money tanto più il suo prezzo sarà sensibile alle
variabili che contribuiscono a determinare il valore del tempo. |
 |
<<< top
>>>
-
- Copyright
©1999-2000-All rights reserved
Bibliografia: Financial Advisor
Di Lorenzo: Guadagnare in borsa...Ed. IlSole24ore
Pring M. Technical Analysis Explained- Mac Graw Hill
Edwards R.D. Magee j -Technical Analysis of Stocks Trends- Boston
S.Guarino - Introduzione all'analisi Tecnica - Università
popolare Napoli Nord |
- Firma
il GuestBook
- di Salvatore Guarino
|
|

