I coefficienti a e ß
costituiscono uno strumento
molto utilizzato nella valutazione del rischio dei titoli. Dal
punto di vista teoretico forniscono il criterio di riferimento
all'interno di un modello, che inquadra il rapporto tra rischio
e rendimento.
Dal punto di vista operativo, invece, offrono una valutazione
quantitativa di immediata applicabilita' pratica.
Il coefficiente
ß di un titolo fornisce il dato statistico
del comportamento dello stesso rispetto all'indice di riferimento:
puo' essere maggiore di 0 (beta >0) ed in questo caso ci informa
che il titolo varia nella stessa direzione dell'indice o inferiore
(beta <0) indicandoci che varia nella direzione opposta. In
pratica:
Se il coefficiente ß è superiore all'unità
(beta >1) vuol dire che il titolo oscillerà in modo
più che proporzionale rispetto all'indice di riferimento,
sia in aumento che in diminuzione
Se il coefficiente ß è compreso tra 0 e 1 (0 <
beta < 1) il valore del titolo oscillera' meno che proporzionalmente
rispetto all'indice in entrambe le direzioni. Il segno meno (-)
nel beta indica che il titolo oscilla in direzione opposta dell'indice.
Ovviamente, più è lungo l'orizzonte temporale dei
dati presi a riferimento , più è significativo
è il valore del beta del titolo a cui si riferisce.
Da segnalare, alcuni recenti studi per l'utilizzo significativo
di un coefficiente "beta mobile"
con rilevazione a 5 e 7 giorni nella gestione dei Covered Warrant.
Per un esempio operativo scarica il file analisi
cw.xls zippato (82.3Kb) per gentile concessione di Norberto Tranquillo
Il coefficiente
a esprime l'attitudine di un titolo a
variare indipendentemente dall'indice di riferimento (mercato).
Se l'alfa di un titolo mostra un valore positivo, significa che
il titolo è in grado di generare autonomamente un rialzo,
mentre se negativo ci informa della tendenza del titolo a subire
perdite indipendentemente dal trend di mercato.
Il modello
teorico
I coefficienti a e
ß si inquadrano nel Capital Asset Pricing
Model (CAPM) un modello statistico matematico del mercato mobiliare,
che rappresenta una situazione ipotetica ideale e che costituisce
, ovviamente, una semplificazione della realta'. Come tutti i
modelli matematici presentano il difetto della non continua aderenza
al mercato , ma anche il pregio di isolare e far emergere gli
aspetti più rilevanti del fenomeno in esame.
La situazione ipotizzata
del modello CAPM è quella del mercato perfetto dove:
1- esiste una relazione di proporzionalità diretta tra
rischio e rendimento dei titoli;
ossia, i titoli che offrono rendimenti maggiori comportano
un rischio maggiore e viceversa
2- Gli investitori sono tutti uguali nel senso che essi dispongono
tutti delle stesse informazioni, detengono le stesse disponibilità
ed hanno tutti lo stesso scopo: massimizzare il profitto ponendosi
ognuno sulla curva rischio-rendimento in funzione delle propensioni
individuali al rischio
3- Le compravendite non sono gravate da nessun costo accessorio
e/o fiscale
Con questo presupposto
la definizione di beta considera l'ipotesi che tutti i titoli
nel lungo periodo si adatteranno all'indice, ma sul breve, non
tutti seguono lo seguono allo stesso modo. In un giorno mentre
molti titoli salgono, seguendo l'indice, altri lo fanno in modo
più o meno che proporzionale , mentre qualcuno, addirittura
lo fa in senso inverso. Ciò comporta la suddivisione del
rendimento e del rischio dei titoli in due componenti:
1- La componente comune- a tutto il mercato che chiameremo
"sistemica", è attribuibile a fattori macroeconomici,
politici, sociali che sono fuori dal controllo degli investitori.
2- La componente propria del titolo che chiameremo "specifica"
dipende dalla singola situazione del titolo in un certo momento.
Naturalmente le due componenti si sovrappongono, sommandosi e/o
compensandosi , dando luogo al cosiddetto "rischio globale
del titolo". Il frazionamento delle due componenti è
importante per l'asset allocation di un portafoglio, perchè
permette di distinguere una parte ineliminabile da quella specifica
che , invece, si può compensare con un'adeguata diversificazione
dei titoli (settori economici, ciclicità e anticiclicità
...)
L'andamento del
ß risponde, dunque, allo scopo di descrivere
in termini quantitativi l'andamento di un titolo in rapporto
al mercato:
Supponiamo di essere
in possesso di una tabella come la seguente:
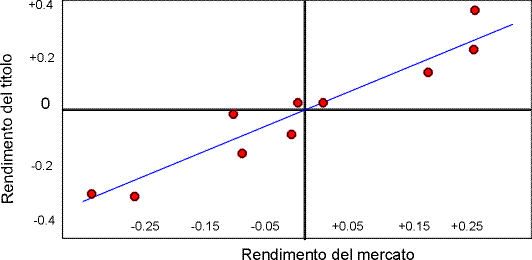
Figura 1
Nella figura sono
riportati i rendimenti del mercato e quelli del titolo svincolati
da qualsiasi riferimento temporale: L'insieme di tali valori
rappresenta, così, tutta l'informazione possibile sul
rapporto tra rendimento del mercato e del titolo, però
in questa forma essa è del tutto inutilizzabile perchè
troppo dispersa.
Occorre, invece concentrare l'informazione dei dati in uno strumento
più immediato e di facile utilizzo. Possiamo, allora,
passare dai dati alla loro MEDIA.
Una parte dell'informazione andrà persa quando la si concentra
tutta in un punto, ma in compenso, potremmo disporre di uno strumento
semplice ed intuitivo.
Nel nostro caso il compito di concentrare l'informazione è
assolto dalla RETTA
di REGRESSIONE, che consente
di sostituire l'insieme dei valori originali con la retta che
ne costituisce l'approssimazione migliore. I calcoli sono molto
semplici; essi forniscono la retta nella forma analitica seguente:
Rt = a + ß xRm
dove Rt e Rm rappresentano
il rendimento del titolo e del mercato, mentre Alfa (a) e Beta
(ß) sono i coefficienti identificativi della retta, ossia
i parametri che stiamo cercando (FIG.2)
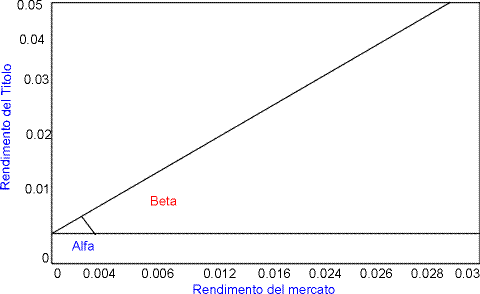
Figura
2
Nella figura , Alfa rappresenta l'ordinata del punto in cui la retta
taglia l'asse verticale e si interpreta come il rendimento del
titolo a prescindere dal rendimento del mercato, ovvero a rendimento
del mercato nullo.
Il coefficiente Beta rappresenta l'inclinazione della retta,
misurata col suo coefficiente angolare ed indica il livello di
reattività, o inversamente, di inerzia, che il titolo
presenta nei confronti del mercato.
Se, ad esempio la
retta è inclinata a 45 °, ed ha, quindi beta=1, cio' significa che a un aumento o
una diminuzione di un 1%, il titolo reagisce con un aumento /diminuzione
analogo: esso riproduce identicamente i movimenti del mercato.
Se la retta è inclinata a meno di 45°, cio' significa
che il titolo reagisce ai movimenti del mercato "attenuandoli";
i titoli di questo tipo hanno un BETA inferiore
a 1 e superiore a 0 (Beta
> 0 <1) e sono detti
"difensivi"; I titoli con Beta maggiore di 1 (B > 1) amplificano i movimenti del mercato
e sono detti "aggressivi".
I valori medi di
Alfa e Beta rispetto a tutti i titoli, sono, ovviamente, quelli
corrispondenti alla globalità del mercato, cioè
0 e 1 rispettivamente. L'interpretazione del Beta
è più delicata di quella dell'Alfa:
per quest'ultimo è infatti possibile affermare che valori
elevati sono preferibili a valori bassi, anche se , ovviamente,
l'alfa è, di solito, molto vicino allo "0".
Per il beta è invece evidente che valori aggressivi sono
preferibili con mercati al rialzo, mentre con mercati al ribasso
sono preferibili valori difensivi, per cui è impossibile
definire in assoluto un valore di Beta migliore.
Un esempio
di coefficienti Alfa - beta e Volatilità tratto dalla
rete:
|
ALERTS |
COEFFICIENTI |
|
Rilevazione al 17.3.1999 |
Rilevazione al 12.3.1999 |
|
TITOLI |
ALFA |
BETA |
VOLATILITA' |
|
ALITALIA |
0,04 |
0,86 |
13,54 |
|
ALLEANZA |
-0,11 |
1,17 |
9,06 |
|
B.CA
DI ROMA |
-0,30 |
1,33 |
15,51 |
|
B.CA FIDEURAM |
-0,03 |
1,35 |
15,18 |
|
B.CA
INTESA |
-0,04 |
1,13 |
12,04 |
|
BENETTON |
-0,05 |
0,96 |
7,51 |
|
COMIT |
-0,06 |
1,25 |
11,18 |
|
COMPART |
-0,17 |
1,17 |
13,72 |
|
EDISON |
0,05 |
0,85 |
13,11 |
|
ENI |
0,01 |
0,77 |
4,65 |
|
FIAT |
-0,18 |
1,20 |
12,52 |
|
FINMECCANICA |
0,09 |
1,03 |
16,62 |
|
GENERALI |
0,03 |
0,99 |
10,50 |
|
H.D.P. |
-0,09 |
0,84 |
11,17 |
|
INA |
0,02 |
1,09 |
9,36 |
|
ITALGAS |
0,12 |
0,56 |
11,61 |
|
MEDIASET |
0,28 |
0,59 |
18,74 |
|
MEDIOBANCA |
-0,08 |
1,39 |
14,08 |
|
MEDIOLANUM |
0,08 |
1,11 |
19,18 |
|
MONTEDISON |
-0,15 |
1,07 |
9,86 |
|
OLIVETTI |
0,24 |
1,06 |
22,94 |
|
PARMALAT |
-0,14 |
1,01 |
10,02 |
|
PIRELLI
SPA |
-0,11 |
1,20 |
8,58 |
|
RAS |
-0,21 |
1,22 |
12,14 |
|
ROLO BANCA 1473 |
-0,04 |
1,21 |
11,35 |
|
SAIPEM |
-0,08 |
0,85 |
6,56 |
|
SAN PAOLO - IMI |
0,04 |
1,15 |
12,71 |
|
TELECOM ITA |
0,15 |
1,15 |
16,68 |
|
TIM |
0,02 |
1,23 |
9,15 |
|
UNICREDITO |
0,04 |
1,39 |
11,20 |
Calcoliamo,
da soli, i coefficienti ALFA e BETA con un foglio Excel
Osserviamo il seguente
foglio Excel:
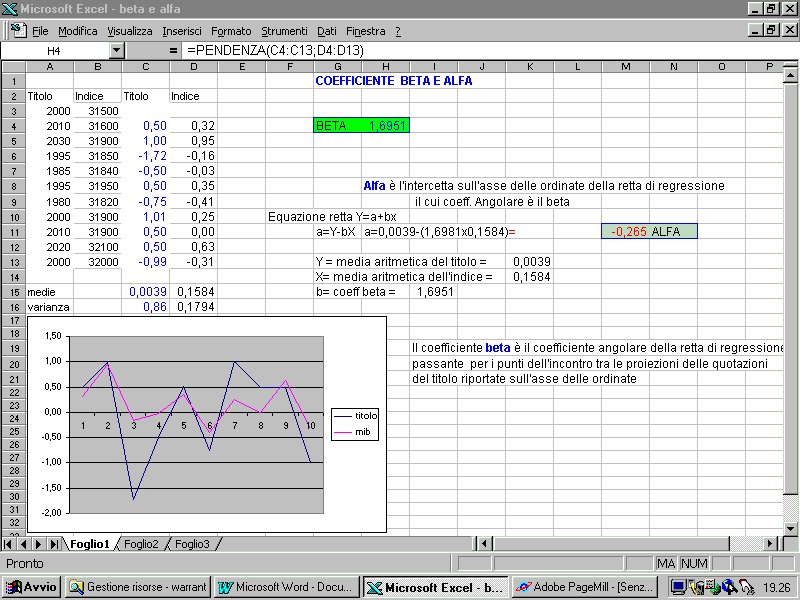
Ipotizziamo di voler
calcolare i coefficienti Alfa e Beta di un titolo azionario rispetto
ad un indice di mercato, per il periodo di 11 sedute borsistiche.
Prepariamo un foglio excel. Indicheremo le quotazione del titolo
(A3:A13), quelle dell'Indice (B3:B13) e nelle colonne C e D le
rispettive variazioni % di ogni seduta rispetto alla precedente.
Calcoliamo le medie delle variazioni e le rispettive Varianze:
Osserviamo subito che la media delle variazioni giornaliere del
titolo è inferiore a quella dell'indice. Ma la varianza
, che osserviamo in direzione opposta, ci dice che il titolo
(VAR 0.86) è ,decisamente, più volatile dell'indice
(VAR 0.1794).
Cerchiamo
il valore del Beta.
Abbiamo definito il beta: il coefficiente angolare della retta
di regressione passante per i punti dell'incontro tra la proiezione
delle quotazioni del titolo riportate sull'asse delle ordinate:
dunque
calcoliamo il Beta con la funzione Excel "PENDENZA dell'intervallo
delle variazioni % del titolo (C4:C13) rispetto a quelle dell'indice
(D4:D13)
Risultato
Beta = 1.6951
Il valore > 1 (1.6951) indica un titolo estremamente volatile
nella stessa direzione del trend dell'indice, confrontabile,
visivamente, con il grafico del titolo (linea blu) rispetto all'indice
(linea fucsia).
Calcoliamo
il valore dell'Alfa.
Abbiamo definito l'Alfa: l'intercetta sull'asse delle ordinate
della retta di regressione il cui coefficiente angolare è
il Beta - dunque :
Possiamo formulare
l'equazione della retta nel seguente modo: Y= a
+ß x ind
ossia a =
Y- ß x
ind sapendo che: Y = Media
aritmetica del titolo = 0.0039
ind = " "
" indice = 0.1584
ß =
coefficiente Beta = 1.6951
a
= Y- ß
x ind =0.0039-(1.6981
x 0.1584) = -0.265 (Risultato ALFA)
|
|

