Il valore
di opzioni e warrant è stato oggetto di numerosi studi
matematici. Il metodo più conosciuto è probabilmente
il modello di Black e Scholes.
Secondo tale modello è possibile determinare il valore
di equilibrio di una opzione o warrant in funzione delle seguenti
sei variabili:
|
1.
Livello corrente del sottostante |
|
2. Strike Price |
|
3. Vita residua |
|
4. Tasso di interesse di periodo |
|
5. Rendimento atteso |
|
6. Volatilità attesa |
Qui di seguito
riportiamo la formula di Black e Scholes per gli amanti della
matematica.
Per il calcolo del prezzo teorico di un warrant:
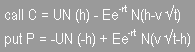
dove:

C = valore teorico warrant call
P = valore teorico warrant put
U = prezzo dell'attività sottostante
E = prezzo di esercizio (strike)
t = tempo residuo alla scadenza (in anni)
v = volatilità dell'attività sottostante il warrant
su base annua
r = tasso di interesse privo di rischio
e = base del logaritmo naturale
In = algoritmo naturale
N(x) = funzione di densità
N'(x) = distribuzione "normale" di probabilità
= 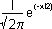
Qualora l'attività
sottostante sia un'azione per la quale ci si aspetta il pagamento
di dividendi durante la vita del relativo warrant, allora la
variabile U viene definita come segue:
 dove:
dove:
d = stima dei dividendi attesi durante la vita del relativo warrant
ti = intervalli temporali relativi alla distribuzione di dividendi
La tabella
qui sotto evidenzia il senso della relazione tra i principali
fattori di mercato ed il valore del warrant. Il segno + segnala
una relazione positiva tra la variabile ed il warrant (ad esempio,
al crescere del valore del sottostante - coeteris paribus- il
valore di un call warrant aumenta). Viceversa il segno - individua
quelle combinazioni variabili/warrant caratterizzate da una correlazione
negativa, per cui al crescere di una variabile corrisponde un
calo del prezzo del corrispondente warrant.
Ad esempio: al trascorrere del tempo qualsiasi warrant perde
valore, ferme restando tutte le altre variabili.
Le prime cinque variabili (livello del sottostante, strike price,
vita residua, tasso di interesse, rendimento atteso) sono conosciute
con certezza.
La sesta rimane l'unica variabile sconosciuta. La stima della
volatilità attesa avviene sulla base di analisi di serie
storiche e/o aspettative. Una volta fissata una stima di questa
variabile è possibile determinare il valore di una opzione
o warrant.
|
Livello del sottostante |
Delta (d) |
+ - |
|
Strike Price |
|
+ - |
|
Vita residua |
Theta (t) |
- - |
|
Tasso di interesse |
Rho (r) |
+ - |
Rendimento atteso (dividendi,
tasso di interesse, valuta estera,
rendimento operazione) |
Phi (j) |
- + |
|
Volatilità |
Vega (u) |
+ + |

