Fisica

      

 

Costanti Fisiche

Unità Misura

Esercizi Fisica

Applet Java

 Test

Quesiti

  
 

Elettrostatica                                       

 
               
 

Esercizio n. 1

            
 

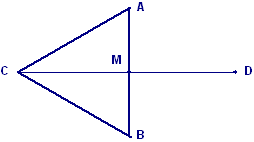
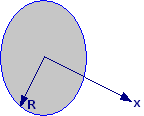
Tre cariche uguali, q = 0,2 C, si trovano ai vertici di un triangolo equilatero ABC di lato L = 15 cm. Calcolare:
a)  Il campo elettrico in M, punto medio di AB.
b)  La d.d.p. tra M e D (punto simmetrico di C rispetto ad AB nel piano del triangolo).
c)  L’energia cinetica, acquistata in M da un elettrone che parte da D, con velocità iniziale nulla ( e = 1,6∙10–9 C).

  
 

R.: 1,07∙1011 V/m ; 3,09∙1010 V ; 4,24∙10–9 J ;

 

  
               
 

Esercizio n. 2

            
 

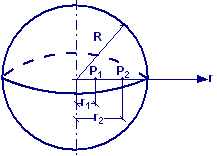
Quattro protoni ( mp = 1,67∙10–27 kg, q = 1,6∙10–19 C) sono disposti ai vertici di un quadrato di lato L = 2∙10–9 m.
Un altro protone si trova inizialmente in A, sulla perpendicolare al quadrato passante per il suo centro O, ad una distanza OA = h = 2∙10–9 m .Calcolare:
a)  L’energia potenziale del quinto protone in funzione della distanza h dal centro.
b)  La minima velocità iniziale che il quinto protone deve avere in A per raggiungere il centro.
c)  L’accelerazione in A ed in C.

 
 

 
               
 

Esercizio n. 3

            
 

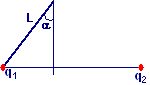
Una sferetta conduttrice di carica q1 = 62,0∙10−8 C e massa m = 98.0 g viene sospesa ad un filo di lunghezza L.

Una seconda sferetta conduttrice con carica  q2 = 6,6∙10−7 C viene avvicinata a q1.  Quando la distanza tra i centri delle sferette vale d = 7,4 cm ed il segmento che le congiunge è perfettamente orizzontale, l’angolo che il filo forma con la verticale vale  α (gradi). Determinare α.
 

  
 

R.: 34. 945° ;

  
               
 

Esercizio n. 4

            
 

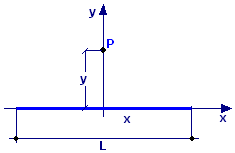
Una sbarretta di lunghezza L = 1,68 m ha una densità lineare di carica λ = 80,0∙10–10 C/m.
Calcolare il campo elettrico in un punto P lungo l’asse della sbarretta ad una distanza d = 32,0 cm da un estremo.

  
 

R.: 188,8 N/C;

  
               
 

Esercizio n. 5

            
 

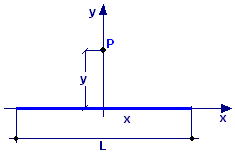
Un elettrone viene posto in quiete sull’asse di una sbarretta di lunghezza L molto grande, uniformemente carica con densità λ, ad una distanza y dal centro della sbarretta. Determinare il modulo della forza elettrostatica a cui è soggetto l’elettrone, assumendo L >> y.

(λ = 75,0∙109 C/m, y = 438,0 cm, e = –1,6∙10-19 C.

  
 

R.: 49,26 N ;

  
               
 

Esercizio n. 6

            
 

Un elettrone viene posto in quiete sull’asse di una sbarretta di lunghezza L molto grande, uniformemente carica con densità λ, ad una distanza y dal centro della sbarretta. Determinare il modulo del campo elettrostatico a cui è soggetto l’elettrone, assumendo L >> y.

(λ = 97,0∙10–10 C/m, y = 102,0 cm, e = –1,6∙10-19 C).

  
 

R.: 170,99 N/C ;

 
               
 

Esercizio n. 7

            
 

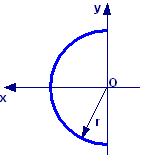
Un anello di raggio R è uniformemente carico con carica totale q = –87,0∙109 C.
Determinare il raggio dell’anello R affinché un elettrone posto sull’asse dell’anello ad una distanza x = 108,0 cm dal centro dell’anello stesso, sia soggetto ad una forza pari ad 1N. (e = –1.6∙10−19 C)

  
 

R.: 5,0169 m ;

  
               
 

Esercizio n. 8

            
 

Una bacchetta di lunghezza L = 14,0 cm, uniformemente carica, è piegata a forma di semicerchio. Se la bacchetta possiede una carica totale q = –7,50 μC, trovare modulo e direzione del campo elettrico nel centro del semicerchio O.

  
 

R.: 2,16∙107 N/C ;

  
               
 

Esercizio n. 9

            
 

Una carica q = 86,0∙10−8 C è posta sull’asse di un disco uniformemente carico con densità superficiale di carica

σ = 431,0∙10−5 C/m2 a distanza x = 0,5 m dal centro del disco. Il raggio del disco è R = 0,5 m.

Determinare il modulo della forza a cui è sottoposta la carica q.

 

  
 

R.: 61,32 N ;

  
               
 

Esercizio n. 10

            
 

Una carica q = 58,0∙10−8 C è posta in prossimità del centro di un disco uniformemente carico con densità superficiale di carica

σ = 490,0∙10−5 C/m2. Determinare il modulo della forza a cui è sottoposta la carica q.

 

  
 

R.: 160,53 N ;

  
               
 

Esercizio n. 11

            
 

Una carica q = 82,0∙10−12 C di massa m = 2,1 g viene posta in quiete al centro di due piani indefiniti paralleli uniformemente carichi con densità di carica superficiale positiva l’uno e negativa l’altro, in valore assoluto pari a σ = 18,0∙10−9 C/m2, posti a distanza d = 2,8 mm. Determinare il tempo impiegato dalla carica a raggiungere il piano con carica negativa e la relativa velocità (si trascuri l’effetto della forza peso).

  
 

R.: 5,938 s ; 4,71·10–4 m/s ;

 
               
 

Esercizio n. 12

            
 

Una carica q = 96,0∙10−9 C viene posta in quiete in prossimità del piano positivo di due piani indefiniti paralleli uniformemente carichi con densità di carica superficiale positiva l’uno e negativa l’altro, in valore assoluto pari a σ = 31,0∙10−3 C/m2, posti a distanza d. Determinare la distanza d tale che q giunga sul piano negativo con energia cinetica Ek = 2,3 J (si trascuri l’effetto della forza peso).

 

  
 

R.: 6,84∙10–3 m ;

 
               
 

Esercizio n. 13

            
 

Un elettrone (q = 1,6∙10−19 C, m = 9,1∙10−31 kg ) ha una velocità iniziale vi = 2,0∙106 m/s nella direzione x. Esso entra con questa velocità in un campo elettrico uniforme la cui intensità E = 100 N/C è orientata nella direzione y. Calcolare:
a)  L’accelerazione dell’elettrone.
b)  Quanto tempo impiega l’elettrone per percorrere 10 cm nella direzione x.
c)  Di quale distanza ed in quale verso è deviato l’elettrone dopo aver percorso 10 cm nella direzione x.
 

  
 

R.: –7,03∙1013 m/s2 ; 50 ns ; 8,8 cm ; 

 
               
 

Esercizio n. 14

            
 

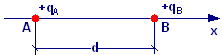
Due cariche elettriche puntiformi positive qA = q e qB = 2∙q si trovano rispettivamente nei punti A e B distanti d = 2,00 m l’uno dall’altro. In quale punto deve essere posta una terza carica qx negativa, lungo la retta passante per A e B, in modo tale che la risultante delle forze agenti su di essa sia nulla?

 

  
 

R.: 0,828 m ;

 
               
 

Esercizio n. 15

            
 

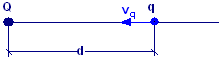
Una piccola sfera di plastica di massa m = 3,0 g e carica elettrica positiva q = 2,0 μC viene lanciata contro una sfera fissa, avente una carica elettrica positiva Q = 4,0 μC distribuita uniformemente nel suo volume.

La velocità della sferetta di plastica, ad una distanza d = 4,0 m dal centro della sfera fissa valga vq = 4,0 m/s. Calcolare la distanza fra le due sfere nel punto di massimo avvicinamento.
 

  
 

R.: 1,7 m ;

 
               
 

Esercizio n. 16

            
 

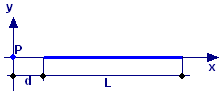
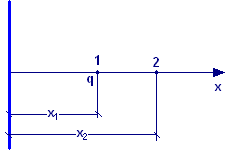
Determinare la variazione di energia potenziale di una carica q = 71,0∙10−9 C che si porta da una distanza x1 = 42,0 cm ad una distanza x2 = 62,0 cm da un filo rettilineo indefinito, uniformemente carico con densità lineare di carica σ = 35,0∙10−3 C/m.

 

  
 

R.: –17,39 J ;

 
               
 

Esercizio n. 17

            
 

Due cariche q1 = 64,0∙10−9 C e q2 =36,0∙10−9 C sono poste nelle posizioni (4,0 ; 4,0 ; 2,0) e (3,0 ; 3,0 ; 9,0) (in metri). Determinare il potenziale nel punto P(1,1,1).

 

  
 

R.: 170,1 V ;

 
               
 

Esercizio n. 18

            
 

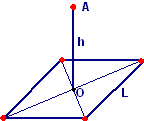
Tre cariche uguali q sono poste nei vertici di un triangolo equilatero di lato L. Determinare il potenziale elettrostatico generato al centro del triangolo. (q = 3,9∙10−10 C, L = 27,8 cm).

 
 

R.: 65,51 V ;

 
               
 

Esercizio n. 19

            
 

Determinare l’energia elettrostatica di un sistema costituito da due cariche q1 = 7,8∙10−6 C e q2 = 8,6∙10−6 C poste ad una distanza

d = 13. 6 cm.
 

  
 

R.: 4,43 J ;

 
               
 

Esercizio n. 20

            
 

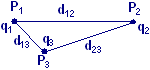
Determinare l’energia potenziale elettrostatica di un sistema costituito da tre cariche q1 = 7,8∙10–6 C, q2 = 8,6∙10–6 C e

q3 = 4,2∙10–6 C situate rispettivamente nei punti P1 , P2 e P3 le cui distanze tra loro siano d12 = 16,2 cm, d13 = 5,4 cm

e d23 = 7,8 cm.
 

  
 

R.: 13,34 J ;  

  
               
 

Esercizio n. 21

            
 

Determinare l’energia potenziale di una carica q = 7,6∙10−5 C posta sull’asse di un anello di raggio R = 24,8 cm uniformemente carico positivamente con carica q1 = 1,09∙10−4 C, a distanze x = 33,2 cm.

 

  
 

R.: 179,67 m ;  

  
               
 

Esercizio n. 22

            
 

Determinare il potenziale nel centro di un disco di raggio R = 10,3 cm uniformemente carico, con densità superficiale di carica

σ = 4,1∙10−10 C/m2.

 

  
 

R.: 2,38 V ;  

  
               
 

Esercizio n. 23

            
 

Due piani indefiniti paralleli uniformemente carichi con densità superficiale di carica  σ  e –σ  (σ = 4,1∙10−10  C/m2), sono posti ad una distanza  d = 60,2 cm. Determinare la differenza di potenziale tra i due piani.

  
 

R.: 27,87 V ;  

  
               
 

Esercizio n. 24

            
 

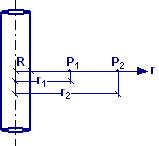
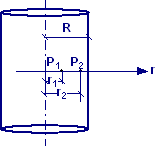
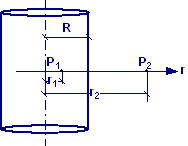
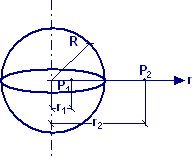
Una distribuzione spaziale continua e uniforme di densità pari a ρ = 1,0∙10−8 C/m3 ha forma cilindrica di raggio R = 72,8 cm. Determinare la differenza di potenziale VP1 – VP2 tra due punti P1 e P2 distanti dall’asse r1 = 124,8 cm ed r2 = 145,8 cm, rispettivamente.
 

  
 

R.: 46,54 V ;  

  
               
 

Esercizio n. 25

            
 

Una distribuzione spaziale continua e uniforme di densità pari a ρ = 8,0∙10−9 C/m3 ha forma cilindrica di raggio R = 69,3 cm. Determinare la differenza di potenziale VP1 – VP2 tra due punti P1 e P2 distanti dall’asse r1 = 18,7 cm ed r2 = 34,3 cm, rispettivamente.

 
 

R.: 18,68 V ;  

  
               
 

Esercizio n. 26

            
 

Una distribuzione spaziale continua e uniforme di densità pari a ρ = 5,0∙10−9 C/m3 ha forma cilindrica di raggio R = 6,0 cm. Determinare la differenza di potenziale VP1 – VP2 tra due punti P1 e P2 distanti dall’asse r1 = 3,4 cm ed r2 = 12,3 cm, rispettivamente.

 
 

R.: 1,075 V ;  

  
               
 

Esercizio n. 27

            
 

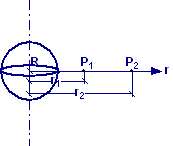
Una distribuzione spaziale continua e uniforme di densità pari a ρ = 3,6∙10−9 C/m3 ha forma sferica di raggio R = 56,3 cm. Determinare la differenza di potenziale VP1– VP2 tra due punti P1 e P2 distanti dal centro della sfera r1 = 97,8 cm ed r2 = 138,0 cm, rispettivamente.

 
 

R.: 7,20 V ;  

  
               
 

Esercizio n. 28

            
 

Una distribuzione spaziale continua e uniforme di densità pari a ρ = 2,0∙10−9 C/m3 ha forma sferica di raggio R = 80,5 cm. Determinare la differenza di potenziale VP1 – VP2 tra due punti P1 e P2 distanti dal centro della sfera r1 = 5,6 cm ed r2 = 51,5 cm, rispettivamente.

 
 

R.: 9,87 V ;  

  
               
 

Esercizio n. 29

            
 

Una distribuzione spaziale continua e uniforme di densità pari a ρ = 8,2∙10−9 C/m3 ha forma sferica di raggio R = 41,1 cm. Determinare la differenza di potenziale VP1 – VP2 tra due punti P1 e P2 distanti dal centro della sfera r1 = 9,1 cm ed r2 = 89,5 cm, rispettivamente.

 
 

R.: 52,99 V ;  

  
               
 

Esercizio n. 30

            
 

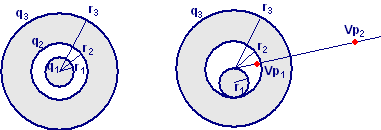
Una carica q = 1,5 pC è posta al centro di una cavità sferica di raggio R = 15.0 cm, praticata all’interno di un blocco di metallo esteso. Calcolare:
a)  il campo elettrico E1 a distanza r1 = 3.6 cm dalla carica.
b)  il campo elettrico E2 a distanza r2 = 23 cm dalla stessa.

  
 

R.: 10,407 V/m ; 0,0 V/m ;  

  
               
 

Esercizio n. 31

            
 

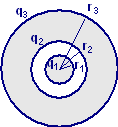
Un conduttore sferico, di raggio r1 = 10 cm, è concentrico ad un conduttore sferico cavo di raggio interno r2 = 33 cm e raggio esterno r3 = 99 cm. Una carica q = 4,7 nC è depositata sul conduttore interno. Calcolare le cariche q1 , q2 , q3 presenti sulle tre superfici sferiche e la differenza di potenziale tra i due conduttori.

  
 

R.: 4.7∙10−9 C ; –4.7∙10−9 C ; 4.7∙10−9 C ; 294,55 V ;  

  
               
 

Esercizio n. 32

            
 

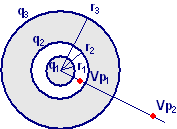
Un conduttore sferico, di raggio r1 = 17 cm, è concentrico ad un conduttore sferico cavo di raggio interno r2 = 59 cm e raggio esterno r3 = 116 cm. Una carica q = 9,4 nC è depositata sul conduttore interno. Calcolare la differenza di potenziale tra due punti VP1 e VP2 a distanza d1 = 28,0 cm e d2 = 329 cm dal centro della sfera cava.
 

  
 

R.: 205,69 V ;  

  
               
 

Esercizio n. 33

            
 

Un conduttore sferico, di raggio r1 = 18 cm, è concentrico ad un conduttore sferico cavo di raggio interno r2 = 47 cm e raggio esterno r3 = 119 cm.

Una carica q = 10,2 nC è depositata sul conduttore interno. Successivamente la sfera interna viene appoggiata sul fondo della cavità. Calcolare la differenza di potenziale tra due punti VP1 e VP2 a distanze d1 = 23,7 cm e d2 = 160 cm dal centro della sfera cava.
 

  
 

R.: 19,74 V ;  

  
               
 

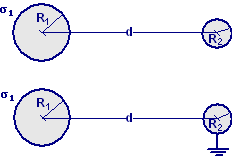
Esercizio n. 34

            
 

Una sfera conduttrice S1 di raggio R1 = 1,1 m è carica uniformemente con densità σ1 = 4,4∙10−9 C/m2. Una sferetta conduttrice S2 di raggio R2 = 18,3 cm viene posta in una posizione tale che i centri delle due sfere distano d = 16,3 m. La sferetta S2 viene collegata a terra tramite un sottile filo conduttore in modo che il suo potenziale sia nullo. Si determini la densità di carica elettrica σ2 (in C/m2) sulla sferetta S2.

  
 

R.: −1,7848∙10−9 C/m2 ;  

  
               
 

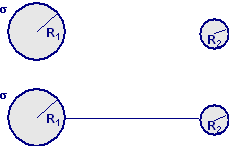
Esercizio n. 35

            
 

Si considerino 2 sfere conduttrici S1 e S2 di raggi rispettivamente R1 ed R2 = 2∙R1. Le due sfere sono molto distanti l’una dall’altra in maniera da non perturbarsi reciprocamente.

Inizialmente la sfera S1 viene caricata con una carica q = 3,6∙10−9 C ad un potenziale V = 41,0 V, mentre S2 è scarica. Le 2 sfere vengono collegate con un lungo e sottile cavo conduttore. Si calcolino i nuovi valori delle cariche elettriche e del potenziale della sfera S2 [si consideri V∞ = 0].
 

  
 

R.: 2,4∙10−9 C ; 1,2∙10−9 C ; 13,667 V ;  

  
               
 

Esercizio n. 36

            
 

Si considerino 2 sfere conduttrici S1 e S2 di raggi rispettivamente R1 ed R2 = ½∙R1.  Le due sfere sono molto distanti l’una dall’altra in maniera da non perturbarsi reciprocamente. 

Inizialmente la sfera S1 viene caricata con una densità di carica elettrica σ = 2,9∙10−7 C/m2 , mentre S2 è scarica. Le due sfere vengono collegate con un lungo e sottile cavo conduttore. Si calcolino i nuovi valori della densità di carica elettrica ( in C/m2 ) su S1 ed S2 .
 

  
 

R.: 1,9333·10−7 C/m2 ; 3,8667·10−7 C/m2 ; 

  
               
 

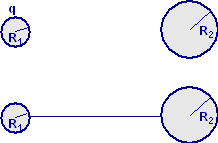
Esercizio n. 37

            
 

Si considerino 2 sfere conduttrici S1 e S2 di raggi rispettivamente R1 = 0,6 m ed R2 = 2,7 m. Le due sfere sono molto distanti l’una dall’altra in maniera da non perturbarsi reciprocamente. Inizialmente la sfera S1 viene caricata con una carica elettrica q = 7,2∙10−7C , mentre S2 è scarica. Le due sfere vengono collegate con un lungo e sottile cavo conduttore. Si calcolino il valore del potenziale a cui si trovano le sfere [si consideri V∞ = 0] e la variazione di energia elettrostatica fra la configurazione finale e quella iniziale.
 

  
 

R.: 1961,2 V ; –3,177·10−3 J ;