Link

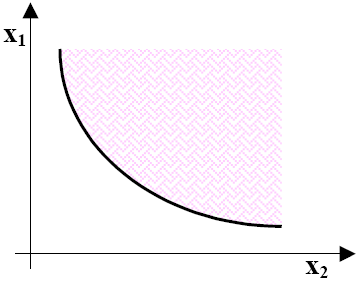
Notizie sulla finanza, sui mutui delle banche, sui mutui online, sui prestiti personali e sull'economia. 

Secondo l'economista italiano Vilfredo Pareto il piacere non può essere misurato e al concetto di scala di utilità va sostituito quello di curva di indifferenza. In particolare all’approccio Cardinalista occorre sostituire quello Ordinalista, che rappresenta la premessa dell’impostazione assiomatica che stiamo per esaminare. Non potendo quantificare l'utilità, dobbiamo parlare, delle preferenze del consumatore.

Supponiamo che, dati due beni (1 e 2) e due qualsiasi panieri di consumo (h1, h2) e (g1, g2), il consumatore possa ordinarli secondo la loro desiderabilità. Il consumatore cioè può stabilire che uno dei panieri è strettamente migliore dell'altro, oppure può ritenere di essere indifferente tra i due.

Useremo il simbolo > per indicare che un paniere è strettamente preferito all'altro. Se il consumatore preferisce un paniere ad un altro, ciò significa che, avendone l'opportunità, sceglierà il paniere preferito. Se il consumatore sceglie sempre (h1, h2) quando è disponibile (g1, g2), è naturale affermare che egli preferisce (h1, h2) a (g1,g2). Per indicare che il consumatore è indifferente tra i due panieri, usiamo il simbolo ∼ e scriviamo (h1, h2) ∼ (g1, g2): ciò significa che il consumatore è ugualmente soddisfatto sia che consumi il paniere (h1, h2) sia che consumi (g1, g2). Dati due panieri di beni, se il consumatore ne preferisce uno all'altro oppure è indifferente tra i due, diciamo che per il consumatore esiste una relazione di preferenza debole tra (h1, h2) e (g1, g2) e la scriviamo come (h1, h2) ≥ (g1, g2).

ASSUNZIONI SULLE PREFERENZE. In genere, gli economisti formulano ipotesi sulla «coerenza» delle preferenze dei consumatori. Ad esempio, sembra contraddittoria una situazione in cui (h1, h2) > (g1, g2) e, contemporaneamente, (g1, g2) > (h1, h2): infatti, ciò significherebbe che il consumatore preferisce strettamente il paniere (h1, h2) al paniere (g1, g2) …. e viceversa.

I principali «assiomi» che garantiscono la razionalità del consumatore sono:

♦ Completezza. In questo caso, assumiamo che sia possibile confrontare sempre due panieri qualsiasi cioè, che dati due panieri qualsiasi (h1, h2) e (g1, g2), è sempre (h1, h2) > (g1, g2) , oppure (h1, h2) < (g1, g2), oppure il consumatore è indifferente tra i due panieri. Questo assioma significa che il consumatore è in grado di effettuare una scelta fra due panieri dati.

♦ Riflessività. Assumiamo che ogni paniere sia desiderabile almeno tanto quanto sé stesso: (h1, h2) ≥ (h1, h2).

♦ Transitività. Se (h1, h2) ≥ (g1, g2) e (g1, g2) ≥ (z1, z2), allora assumiamo che (h1, h2) ≥ (z1, z2). In altri termini, se il consumatore ritiene che H sia desiderabile almeno tanto quanto G e che G sia desiderabile almeno tanto quanto Z, allora per il consumatore H è desiderabile almeno tanto quanto Z.

I primi tre assiomi bastano a derivare le funzioni di utilità. Esistono poi ipotesi che possono essere formulate relative al profilo psicologico degli individui:

♦ Principio della non sazietà o della non saturazione. Assumiamo, in questo caso, che «più è meglio». Più precisamente, se (h1, h2) è un paniere di beni e (g1, g2) è un altro paniere che contiene almeno la stessa quantità di entrambi e una quantità addizionale di uno solo, allora (g1, g2) > (h1, h2). Questa è chiamata anche ipotesi di monotonicità delle preferenze.

♦ L’ipotesi dell’egoismo. Gli individui tengono conto solo della propria utilità o soddisfazione, cioè la solidarietà e l’altruismo non influenzano le scelte economiche.

♦ «La media è preferita agli estremi». Se individuiamo due panieri (h1, h2) e (g1, g2) sulla stessa curva di indifferenza e ne consideriamo una media aritmetica:

( ½ h1 + ½ g1; ½ h2 + ½ g2 )

tale media sarà strettamente preferita ai due panieri estremi, o almeno altrettanto buona. Il paniere corrispondente alla media ponderata contiene esattamente la quantità media del bene 1 e la quantità media del bene 2 dei due panieri: giace, pertanto, a metà della retta che congiunge il paniere-x al paniere-y.

In realtà, questa ipotesi sarà mantenuta per qualsiasi peso t compreso fra 0 e 1, non solo ½. Assumiamo, quindi, che se (h1, h2) ∼ (g1, g2), allora:

( t h1 + (1 −t) g1; t h2 + (1 −t) g2 ) ≥ (h1, h2)

per qualsiasi valore di t tale che 0 ≤ t ≤ 1. La media ponderata dei due panieri dà al paniere-h un peso uguale a t volte quello assegnato al paniere-g. La distanza tra il paniere-h e il paniere medio è esattamente una frazione t della distanza tra il paniere-h e il paniere-g, lungo la retta che li congiunge.

LE CURVE DI INDIFFERENZA. Consideriamo, ora, un individuo che consuma due beni, il bene 1 e il bene 2, e riportiamo le quantità di questi su di una coppia di assi cartesiani. Ciascuna combinazione possibile dei due beni (che chiameremo, appunto, paniere) è rappresentata da un punto nel piano.

Chiameremo, allora, curva di indifferenza l'insieme delle combinazioni di x1 e x2 che danno all'individuo la stessa utilità, ovvero che il consumatore dichiara essere indifferenti nei confronti del paniere dato.

L'area ombreggiata rappresenta l'insieme di tutti i panieri almeno altrettanto desiderabili di (x1; x2) e costituisce l'insieme preferito debolmente. Inoltre, dobbiamo dire che non vi sarà una sola curva di indifferenza. Infatti, se consideriamo il paniere C, anche in questo caso vi saranno molti panieri indifferenti rispetto a quest'ultimo, e, congiungendo tutti i punti che rappresentano tali panieri, otteniamo una nuova curva di indifferenza, più alta (cioè più spostata verso destra) rispetto alla precedente. I panieri situati sulla nuova curva sono indifferenti tra loro, ma sono preferiti a tutti quelli che giacciono sulla curva più bassa. Avremo, quindi, infinite curve di indifferenza, cioè una mappa di curve di indifferenza.

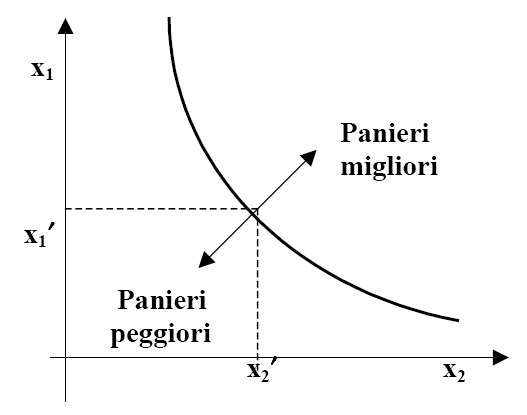
PROPRIETÀ DELLE CURVE DI INDIFFERENZA. Ogni curva di indifferenza è decrescente perché la diminuzione del consumo di un bene va compensata con l'aumento di quello dell'altro, se si vuole che la soddisfazione del soggetto rimanga costante. È l'assioma di non sazietà che comporta che le curve di indifferenza abbiano un'inclinazione negativa. Consideriamo, infatti, dapprima un paniere (x1′, x2′), come nel grafico:

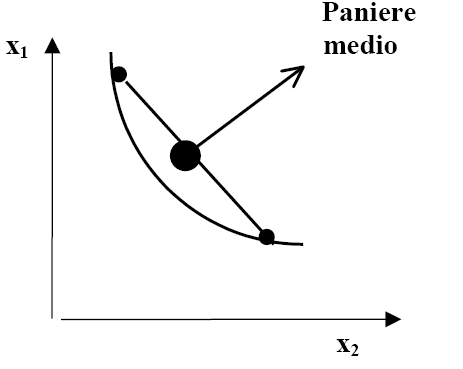
Inoltre, ogni curva di indifferenza ha la convessità rivolta verso l'origine degli assi perché man mano che la persona consuma una quantità minore del bene 1, occorrono quantità via via maggiori del bene 2 per compensarla della diminuzione di una data quantità del primo bene. Tale proprietà deriva dall'assioma che la media è preferita agli estremi. Supponiamo che (h1, h2) e (g1, g2) siano indifferenti: se le medie sono preferite agli estremi, tutte le medie ponderate di (h1, h2) e (g1, g2) saranno preferite debolmente a (h1, h2) e (g1, g2). Quindi, dovremmo avere :

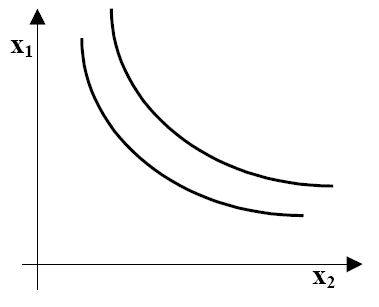
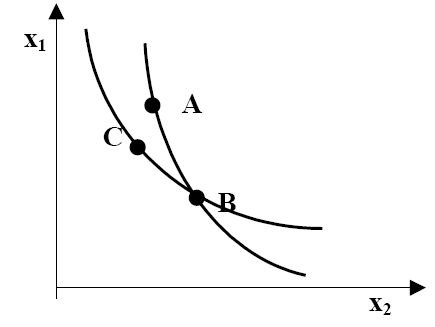
Infine, le curve di indifferenza non si intersecano mai fra loro, e ciò si deriva dall'assioma della transitività. Consideriamo questo grafico:

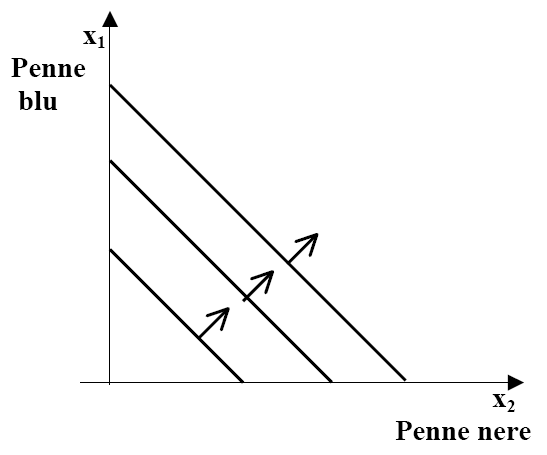
Il paniere A è preferito al paniere C per il principio della non sazietà in quanto contiene maggiori quantità di entrambi i beni. Il paniere B appartiene ad entrambe le curve, per cui è indifferente sia rispetto al paniere A sia al paniere C, ma allora il paniere A e il paniere C dovrebbero essere indifferenti tra loro per la proprietà transitiva, mentre, come abbiamo visto, il paniere A è preferito al paniere C. Quindi, le curve di indifferenza non possono mai intersecarsi.

ESEMPI DI PREFERENZE (CURVE DI INDIFFERENZA “ATIPICHE O IRREGOLARI”):

1. Diciamo che due beni sono perfetti sostituti se il consumatore è disposto a sostituire un bene con l'altro ad un saggio costante. Il caso più semplice è quello nel quale i due beni vengono sostituiti in proporzione uno a uno. Supponiamo, ad esempio, di considerare una scelta fra penne blu e penne nere e che il consumatore in questione, desideri le penne indipendentemente dal colore. Scegliamo un paniere di consumo, per esempio (10; 10). Ogni altro paniere che contenga 20 penne è, per questo consumatore, desiderabile tanto quanto (10; 10). In termini matematici, ogni paniere di consumo (x1, x2) tale che x1 + x2 = 20 sarà sulla curva di indifferenza che passa per (10; 10). Le curve di indifferenza di questo consumatore sono pertanto tutte rette parallele con inclinazione −1, come rappresentato in figura:

I panieri con un maggior numero complessivo di penne sono preferiti ai panieri con un minore numero complessivo di penne: pertanto le preferenze aumentano nella direzione verso l'alto a destra.

È importante notare che nel caso dei perfetti sostituti le curva di indifferenza hanno inclinazione costante. Supponiamo, ad esempio, di considerare le preferenze di un consumatore tra penne nere e coppie di penne blu: le curve di indifferenza relative a questi due beni avranno inclinazione −2, poiché il consumatore sarà disposto a rinunciare a due penne nere in cambio di una coppia addizionale di penne blu.

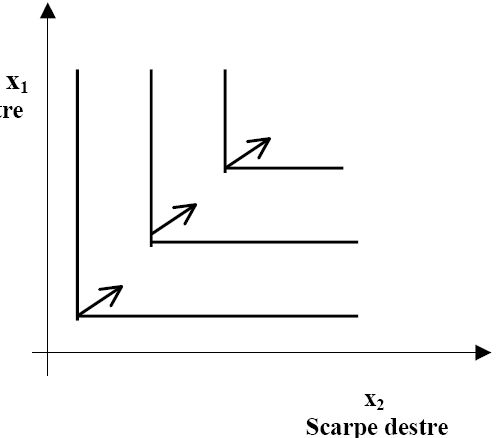
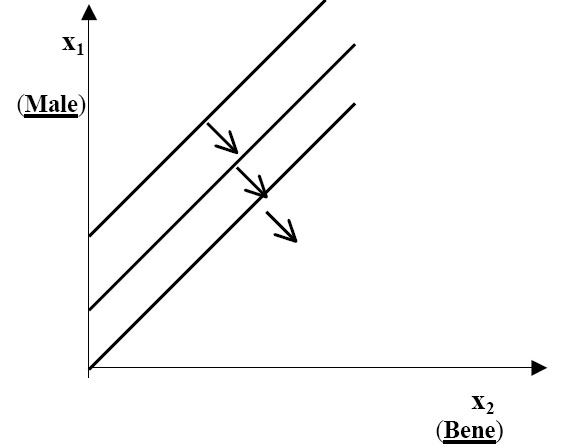
Diciamo che due beni sono perfetti complementi se vengono sempre consumati congiuntamente in proporzioni fisse: in un certo senso, i beni «si completano» a vicenda. Le curve di indifferenza avranno quindi una forma a L, il cui vertice si troverà in corrispondenza del punto in cui il numero delle scarpe sinistre è uguale al numero delle scarpe destre, come in figura:

3. Diciamo che un bene è un bene neutrale quando per il consumatore è indifferente consumarlo o non consumarlo. Nel caso in cui un consumatore sia neutrale nei confronti del bene x1 le curve di indifferenza saranno delle rette verticali, come rappresentato in figura: