A mathematician is a blind man in a dark room looking for a black cat which isn't there.

Charles Darwin

La vera religione è la matematica, il resto è superstizione (detto in altri termini, la matematica è la religione dei poveri di spirito.

Pitagora

-50.000	Traccia di conteggi da parte dell'uomo di Neanderthal
-25.000	Disegni geometrici primitivi da parte dell'uomo di Cro-Magnon
-15.000	Nell'attuale Libano, si sono trovate ossa di animali, risalenti a questo periodo, che mostrano intaccature riunite in gruppi di eguale cardinalità.
-4241	Presunta origine del calendario egiziano
-3000	Numeri geroglifici in Egitto
-1850	Papiro di Mosca: notazione posizionale in Mesopotamia
-1700	Papiro di Rhind: rotolo lungo cinque metri, composto da quattordici fogli di papiro, contiene decine di problemi matematici di vario tipo.
-600	Il greco Talete (624-546 circa) è considerato il fondatore della geometria. Sebbene non abbiamo nessun documento certo, gli vengono attribuiti i teoremi sulla similitudine dei triangoli, in particolare quello che porta il suo nome.
-500	Il greco Pitagora (580-497 circa) è il fondatore di una scuola matematica, filosofica e religiosa con sede a Crotone. Nessun documento scritto ci è pervenuto di questo pensatore. Gli si attribuisce il famoso teorema sui triangoli rettangoli che porta il suo nome.
-400	Il greco Ippocrate (460-377) scrive il primo trattato di geometria. Democrito (460-370), Eudosso (408-353), Archita di Taranto risolvono importanti problemi di geometria e aritmetica). Zenone enuncia i famosi paradossi.
-300	Euclide organizza negli Elementi i teoremi di geometria e di teoria dei numeri ottenuti dalla cultura  matematica greca dell'epoca. Procede per definizioni, postulati e teoremi con una esposizione che è rimasta classica per ogni tempo. Aristotele codifica le leggi del ragionamento logico.
-200	Archimede di Siracusa (287-212) si occupa di aritmetica, algebra, geometria, fisica; risolve importanti problemi sulle equazioni cubiche; anticipa il calcolo logaritmico e il calcolo integrale. Ipparco (190-125) fonda la trigonometria piana e sferica. Apollonio studia le coniche. Eratostene effettua la prima misurazione del diametro della Terra.
-100	Erone compie importanti studi di geometria e di fisica
100	Tolomeo nell'Almagesto tratta problemi di trigonometria piana e sferica.
200	Diofanto studia l'aritmetica, usa i simboli algebrici ed enuncia le regole per risolvere le equazioni di primo e secondo grado
500	Il latino Boezio compie ricerche di logica e geometria.
600	Gli Indiani usano la notazione posizionale e i numeri indù. I Cinesi introducono l'estrazione di radice quadrata.
800	Gli Arabi diffondono la numerazione posizionale indiana, detta poi arabica. L'arabo al-Khuwarizmi compone il trattato Al-giabr wa'l mu kabala, da cui deriva il nome algebra. Dal nome di questo matematico deriva il nome algoritmo.
1000	L'indiano Sridhara dà una chiara esposizione dell'uso del numero 0, affermando che a+0=a, a-0=a, a·0=0, 0·a=0.
1200	L'italiano Fibonacci di Pisa (1175-1240) nel trattato Liber Abaci introduce in Europa il sistema di numerazione arabo, nonché i risultati algebrici della cultura musulmana.
1500	L'italiano Luca Pacioli (1445-1510) scrive il primo trattato generale di aritmetica e algebra, Summa, con un accenno al calcolo delle probabilità e ai logaritmi. Gerolamo Cardano tratta le cosiddette grandezze immaginarie. Niccolò Fontana detto Tartaglia espone la regola per la risoluzione delle equazioni di terzo grado ridotte. Il francese Viète introduce l'algebra simbolica, che permette di scrivere lunghe espressioni algebriche, secondo il metodo moderno.
1600	Napier e Buergi inventano, indipendentemente l'uno dall'altro, i logaritmi. Briggs pubblica le prime tavole dei logaritmi a base 10. Fermat coglie i principi essenziali della geometria analitica. Cavalieri studia il calcolo infinitesimale. Nel 1636 Descartes pubblica il Discours de la méthode che contiene i fondamenti della geometria analitica. Pascal dà le basi della geometria proiettiva e del calcolo delle probabilità. Newton crea il calcolo delle flussioni, poi detto calcolo infinitesimale. Anche Leibniz crea, indipendentemente da Newton, e con simbolismi differenti il calcolo differenziale.
1700	Eulero introduce il calcolo delle variazioni, applicando i metodi del calcolo differenziale alle curve e alle superfici. I Bernoulli e Lagrange sviluppano la teoria delle equazioni integrali e differenziali applicandola alla geometria e alla meccanica
1800	Gauss dimostra il teorema fondamentale dell'algebra: ogni equazione ha tante equazioni quanto è il suo grado. Nel campo della geometria introduce lo studio della curvatura delle superfici e mette in crisi la geometria euclidea. Laplace introduce in modo rigoroso la teoria della probabilità. Cauchy e Weierstrass rendono rigoroso il calcolo infinitesimale. Monge e Poncelet fondano la geometria descrittiva e la geometria proiettiva. Lobacevskij e Bolyai, indipendentemente l'uno dall'altro, studiano una geometria che contraddice il postulato di Euclide sulle parallele. Riemann fonda le geometrie euclidee e non sul concetto di metrica. Boole applica il calcolo algebrico alla logica. Cantor formula la teoria degli insiemi. Klein dà un quadro completo, attraverso la teoria dei gruppi di trasformazioni delle varie geometrie sorte nell'Ottocento: proiettiva, metrica, euclidea, ellititica, iperbolica, topologia. Frege si propone di unificare logica e aritmetica. Peano costruisce una simbologia per il calcolo logico e per le dimostrazioni matematiche. Enriquez organizza in modo rigoroso la geometria proiettiva.
1900	Hilbert dà una formulazione puramente assiomatica della geometria. Ricci-Curbastro e Levi-Civita creano il calcolo differenziale assoluto, strumento utilizzato da Einstein per formulare la teoria della relatività. Russell cera di fondare la matematica su basi puramente logiche. Brouwer in contrapposizione ritiene esclusivamente intuitivi i principi della matematica. Volterra fonda il calcolo funzionale. von Newmann elabora la teoria dei giochi. Goedel dimostra che nei sistemi formali è possibile individuare proposizioni indimostrabili, ne consegue che l'aritmetica non può fondarsi su se stessa. Wiener introduce la cibernetica e la teoria dell'informazione. Thom intraprende lo studio delle catastrofi o del caos, ossia delle trasformazioni improvvise. Mandelbrot espone lo studio dei frattali, forme geometriche irregolari che appaiono simili se osservate su scale diverse.

I matematici di tutti i tempi

LA MATEMATICA GRECA

VI secolo a.C., i fondatori: Talete, geometria; Pitagora, aritmetica.

V secolo a.C., i pitagorici: Filolao (di Crotone), Ippaso di Metaponto, Ippocrate di Chio, Dernocrito di Abdera (l'atomista), gli eleatici (da Elea, città dell'Italia meridionale): Parmenide e Zenone. Il sofista Ippia di Elide, studioso di geometria.

IV secolo a.C. Scuola di Atene. Platone, lavori dell'Accademia; Eudosso di Cnido (creatore, insieme con Antifonte, del «metodo di esaustione», antenato del calcolo integrale). Teodoro di Cirene, Teeteto, Archita di Taranto. E poi Aristotele (logica, ragionamento). Menecmo, Autolico di Pitane. Eudemo di Rodi, il peripatetico, storico della matematica e dell'astronomia.

III secolo a.C., ovvero l'«età aurea» della matematica greca. Il grande trio: Euclide e Apollonio di Perge, ad Alessandria, Archimede a Siracusa. Euclide con i suoi Elementi, Apollonio con le Coniche, e infine Archimede.

A partire dal III secolo avanti Cristo (all'incirca) tutto si concentra ad Alessandria. Siamo nel cosiddetto periodo ellenistico. La matematica greca, nata dopo i viaggi di Talete e Pitagora in Egitto, torna alle origini.

III secolo a.C.: Eratostene di Cirene, matematico, astronomo, geografo e bibliotecario del Museo di Alessandria, effettua la prima misurazione rigorosa della Terra.

II secolo a.C: Ipparco di Nicea, il «padre della trigonometria», e Teodosio di Bitinia, l'astronomo.

I secolo a.C.: Erone di Alessandria, studioso della meccanica.

II secolo dopo Cristo: Claudio Tolomeo, geografo e astronomo, Nicomaco di Cerasa, Teone di Smirne (teoria dei numeri), Menelao di Alessandria (trigonometria sferica).

III secolo: Diofanto di Alessandria, il « padre dell'algebra ».

IV secolo: Pappo di Alessandria, autore di una sintesi della geometria dei secoli precedenti. Teone di Alessandria, geometria, e sua figlia Ipazia, l'unica donna che si sia occupata di matematica nell'antichità.

V secolo: i « grandi commentatori » della matematica greca, Proclo, che commenta Euclide, ed Eutocie di Ascalone, che commenta Apollonio e Archimede.

VI secolo: Severino Boezio, l'ultimo matematico dell'antichità.

MATEMATICI DEL MONDO ARABO DAL IX AL XV SECOLO

Dopo qualche secolo di torpore, tra il V e il VI secolo dell'era cristiana la scienza greca fu ripresa dai matematici arabi che, dopo averla assimilata, la misero a frutto. Grazie al passaggio attraverso la cristiana Bisanzio, la matematica della pagana Alessandria giunse a Baghdad, capitale dell'Islam.

Gli eruditi arabi, specie quelli del IX e del X secolo, avevano la particolarità di essere grandi matematici e traduttori sopraffini al contempo. Si lanciarono così in un'impresa immensa, la traduzione dei testi dei matematici greci: Euclide, Archimede, Apollonio, Menelao, Diofanto, Tolomeo. Questo lavoro li mise in condizione di assimilare il sapere matematico dell'antichità e di arricchirlo in misura considerevole, creando nuovi settori della matematica sconosciuti ai greci. Tuttavia quegli studiosi attinsero anche ad altre fonti, soprattutto a quella indiana.

Una caratteristica che avevano in comune con i greci era il fatto di essere studiosi «a 360 gradi»: esperti di matematica, medicina, astronomia, filosofia e fisica. Sono stati i matematici arabi a creare l'algebra, il calcolo combinatone, la trigonometria.

Inizi del IX secolo. Baghdad, al-Khwàrizmi (algebra, equazioni di primo e secondo grado a un'incognita). Egitto, Abù-Kàmil, amplia il campo dell'algebra (sistemi di più equazioni a più incognite). Al-Farisi getta le basi della teoria sulla divisibilità dei numeri, affermando che: «ogni numero si scompone necessariamente in un numero definito di fattori primi, dei quali è il prodotto ».

Seconda metà del IX secolo. Geometria, sempre a Baghdad, i tre fratelli Banu Musa. Poi altri tre saggi, Thabit ibn-Qurra, al-Nayrizi e Abù al-Wafa (calcolo delle aree; parabola, ellisse, teoria delle frazioni; fondatore della trigonometria come settore autonomo della matematica).

Fine del X secolo. Due grandi sapienti, il geografo al-Biruni, astronomo e medico, e Ibn al-Haytham, l'«al-Hazen» degli occidentali (teoria dei numeri, geometria, metodi infinitesimali, ottica, astronomia. Ma non algebra!)

Ibn al-Khawwàm formula il problema che più tardi diventerà la celebre congettura di Fermat: un cubo non può essere la somma di due cubi, l'equazione: x³ + y³ = z³ non ammette soluzioni in termini di numeri interi.

Altri due grandi matematici, al-Karaji, alla fine del X secolo, e al-Samawa'l, nel XII, che proseguì l'opera del primo. Al-Samawa'l propone un sistema di 210 equazioni con dieci incognite, e lo risolve! Aritmetizzazione dell'algebra.

Aritmetizzazione dell'algebra: applicazioni all'incognita delle operazioni (+, -, x, :, estrazione delle radici quadrate) che l'aritmetica utilizzava esclusivamente per i numeri. Estensione del calcolo sui numeri al calcolo algebrico.

Al-Karaji studia le potenze algebriche: xⁿ e 1/xⁿ. Al-Samawa'l utilizza le quantità negative, dimostrando la regola fondamentale del calcolo sulle potenze: x^mxⁿ = x^m+n. È uno dei primi a usare la « dimostrazione per induzione » allo scopo di verificare risultati matematici, soprattutto nel campo della teoria dei numeri.

Il calcolo della somma di n numeri primi interi,

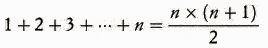
della somma del loro quadrato,

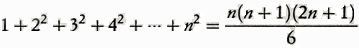
di quella del loro cubo.

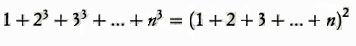
Fine del XI secolo. Omar al-Khayyam, poeta e matematico, grande studioso di algebra.

Fine del XII secolo. Sharaf ai-Din al-Tùsi, anche lui grande studioso di algebra. Cinquecento anni prima dei matematici occidentali, utilizza procedimenti che prefigurano la nozione di derivata.

XIII secolo. Nasir ai-Din al-Tùsi (astronomo, riformatore del sistema tolemaico).

Inizi del XV secolo. Piena maturità della matematica araba; al-Kashi, direttore dell'osservatorio di Samarcanda, realizza una sintesi della matematica araba degli ultimi sette secoli: rapporti tra l'algebra e la geometria, rapporti tra l'algebra e la teoria dei numeri; trigonometria e «analisi combinatoria» (studio dei vari modi per combinare tra loro gli elementi di un insieme); «soluzione di equazioni per radicali» (calcolo delle soluzioni delle equazioni utilizzando soltanto le quattro operazioni e le radici quadrate, cubiche, eccetera).

MATEMATICA IN OCCIDENTE A PARTIRE DAL 1400

XVI secolo. Il grande secolo dell'algebra elementare. Scuola italiana di Bologna, (equazioni di terzo e quarto grado): Niccolò Tartaglia, Gerolamo Cardano, Ludovico Ferrari, Raffaele Bombelli. Scoperta dei numeri complessi. Grandi progressi delle notazioni simboliche, Francois Viète, Simon Stevin.

XVII secolo. Invenzione dei logaritmi: John Napier. La matematica barocca. Algebra: Albert Girard, Thomas Harriot, William Oughtred. Geometria analitica (che stabilisce un nesso tra numeri e spazio per mezzo dell'algebra): Pierre de Fermat, Rene Descartes (Cartesio). Geometria degli indivisibili: Bonaventura Cavalieri, Gilles Personne de Roberval, Pierre de Fermat, Grégoire de Saint-Vincent. Calcolo infinitesimale (calcolo differenziale, calcolo integrale): Isaac Newton, Gottfried Wilhelm Leibniz, Jacques e Jean Bernoulli, Brook Taylor, Colin MacLaurin. Teoria dei numeri: Pierre de Fermat. Calcolo delle probabilità e calcolo combinatorio: Blaise Pascal, Pierre de Fermat, Jacques Bernoulli. Geometria: Gerard Desargues, Blaise Pascal, Philippe de la Hire...

XVIII secolo. L'epoca classica, l'età d'oro dell'« analisi ». Dopo i numeri e le figure, oggetto privilegiato della matematica diventano le funzioni. Equazioni differenziali, studio delle curve, numeri complessi, teoria delle equazioni, calcolo delle variazioni, trigonometria sferica, calcolo delle probabilità, meccanica; Jacques Bernoulli, Leonhard Euler, Jean Le Rond d'Alembert, Alexis Claude Clairaut, Abraham de Moivre, Gabriel Cramer, Gaspard Monge, Joseph-Louis Lagrange, Pierre-Simon de Laplace, Adrian-Marie Legendre. La soluzione di problemi posti all'inizio del secolo da Leibniz e Newton, quadrature, integrazione di equazioni differenziali, ha fatto grandi passi avanti.

XIX secolo. Apertura di nuovi campi matematici, invenzione di nuovi strumenti (i gruppi, le matrici...) L'inizio del secolo è dominato dalla teoria delle funzioni di una variabile immaginaria: Augustin Cauchy, Georg Friedrich Bernhard Riemann, Karl Theodor Wilhelm Weierstrass. L'algebra con Niels Henrik Abel, Evariste Galois, Karl Gustav Jacobi, Ernst Eduard Kummer. La geometria con Jean-Victor Poncelet, Michel Chasles, Félix Klein. E Karl Friedrich Gauss, è chiaro, presente ovunque.

Le geometrie non euclidee: Gauss, Nikolaj Ivanovic Lobacevskij, Janos Bolyai, Georg Friedrich Bernhard Riemann. Il calcolo matriciale: Arthur Cayley. L'algebra booleana (da George Boole). La teoria degli insiemi: Georg Cantor, Richard Dedekind, David Hilbert

(Tratto da "Il teorema del Pappagallo - Denis Guedj - 2003 TEA)