Special Numbers
Perfect numbers
It is not known when perfect numbers were first
studied and indeed the first studies may go back to the earliest times when
numbers first aroused curiosity. It is quite likely, although not certain, that
the Egyptians would have come across such numbers naturally given the way their
methods of calculation worked. Perfect numbers were studied by
Pythagoras
and his followers, more for their mystical properties than for their number
theoretic properties. Before we begin to look at the history of the study of
perfect numbers, we define the concepts which are involved.
Today the usual definition of a perfect number is in
terms of its divisors, but early definitions were in terms of the 'aliquot
parts' of a number.
An aliquot part of a number is a proper
quotient of the number. So for example the aliquot parts of 10 are 1, 2 and 5.
These occur since 1 = 10/10, 2 =
10/5, and 5 = 10/2. Note that 10 is
not an aliquot part of 10 since it is not a proper quotient, i.e. a quotient
different from the number itself. A perfect number is defined to be one which is
equal to the sum of its aliquot parts.
The four perfect numbers 6, 28, 496 and 8128 seem to
have been known from ancient times and there is no record of these discoveries.
6 = 1 + 2 + 3,
28 = 1 + 2 + 4 + 7 + 14,
496 = 1 + 2 +
4 + 8 + 16 + 31 + 62 + 124 + 248
8128 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 127
+ 254 + 508 + 1016 + 2032 + 4064
The first recorded mathematical result concerning
perfect numbers which is known occurs in Euclid's
Elements written around 300BC. It may come as a surprise to many people
to learn that there are number theory results in Euclid's
Elements since it is thought of as a geometry book. However, although
numbers are represented by line segments and so have a geometrical appearance,
there are significant number theory results in the Elements. The result
which is if interest to us here is Proposition 36 of Book IX of the
Elements which states :
If as many numbers as we please beginning from
a unit be set out continuously in double proportion, until the sum of all
becomes a prime, and if the sum multiplied into the last make some number, the
product will be perfect.
Here 'double proportion' means that each number of
the sequence is twice the preceding number. To illustrate this Proposition
consider 1 + 2 + 4 = 7 which is prime. Then
(the sum)
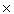 (the last) = 7 (the last) = 7
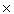 4 = 28, 4 = 28,
which is a perfect number. As a second example, 1 +
2 + 4 + 8 + 16 = 31 which is prime. Then 31 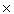 16 = 496 which is a perfect number. 16 = 496 which is a perfect number.
Now Euclid
gives a rigorous proof of the Proposition and we have the first significant
result on perfect numbers. We can restate the Proposition in a slightly more
modern form by using the fact, known to the Pythagoreans, that
1 + 2 + 4 + ... + 2k-1 =
2k - 1.
The Proposition now reads:-
If, for some k > 1, 2k - 1 is
prime then 2k-1(2k - 1) is a perfect
number.
The next significant study of perfect numbers was
made by Nicomachus
of Gerasa. Around 100 AD Nicomachus
wrote his famous text Introductio Arithmetica which gives a
classification of numbers based on the concept of perfect numbers. Nicomachus
divides numbers into three classes, the superabundant numbers which have the
property that the sum of their aliquot parts is greater than the number,
deficient numbers which have the property that the sum of their aliquot parts is
less than the number, and perfect numbers which have the property that the sum
of their aliquot parts is equal to the number (see [8], or [1] for a different
translation):-
Among simple even numbers, some are
superabundant, others are deficient: these two classes are as two extremes
opposed to one another; as for those that occupy the middle position between
the two, they are said to be perfect. And those which are said to be opposite
to each other, the superabundant and the deficient, are divided in their
condition, which is inequality, into the too much and the too little.
However Nicomachus
has more than number theory in mind for he goes on to show that he is thinking
in moral terms in a way that might seem extraordinary to mathematicians today
(see [8], or [1] for a different translation):-
In the case of the too much, is produced
excess, superfluity, exaggerations and abuse; in the case of too little, is
produced wanting, defaults, privations and insufficiencies. And in the case of
those that are found between the too much and the too little, that is in
equality, is produced virtue, just measure, propriety, beauty and things of
that sort - of which the most exemplary form is that type of number which is
called perfect.
Now satisfied with the moral considerations of
numbers, Nicomachus
goes on to provide biological analogies in which he describes superabundant
numbers as being like an animal with (see [8], or [1]):-
... ten mouths, or nine lips, and provided with three
lines of teeth; or with a hundred arms, or having too many fingers on one of
its hands....
Deficient numbers are compared to animals with:-
a single eye, ... one armed or one of his hands has less
than five fingers, or if he does not have a tongue...
Nicomachus
goes on to describe certain results concerning perfect numbers. All of these are
given without any attempt at a proof. Let us state them in modern notation.
(1) The nth perfect number has n digits.
(2)
All perfect numbers are even.
(3) All perfect numbers end in 6 and 8
alternately.
(4) Euclid's
algorithm to generate perfect numbers will give all perfect numbers i.e. every
perfect number is of the form 2k-1(2k -
1), for some k > 1, where 2k - 1 is prime.
(5)
There are infinitely many perfect numbers.
We will see how these assertions have stood the
test of time as we carry on with our discussions, but let us say at this point
that assertions (1) and (3) are false while, as stated, (2), (4) and (5) are
still open questions. However, since the time of Nicomachus
we do know a lot more about his five assertions than the simplistic statement we
have just made. Let us look in more detail at Nicomachus's
description of the algorithm to generate perfect numbers which is assertion (4)
above (see [8], or [1]):-
There exists an elegant and sure method of
generating these numbers, which does not leave out any perfect numbers and
which does not include any that are not; and which is done in the following
way. First set out in order the powers of two in a line, starting from unity,
and proceeding as far as you wish: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512,
1024, 2048, 4096; and then they must be totalled each time there is a new
term, and at each totalling examine the result, if you find that it is prime
and non-composite, you must multiply it by the quantity of the last term that
you added to the line, and the product will always be perfect. If, otherwise,
it is composite and not prime, do not multiply it, but add on the next term,
and again examine the result, and if it is composite leave it aside, without
multiplying it, and add on the next term. If, on the other hand, it is prime,
and non-composite, you must multiply it by the last term taken for its
composition, and the number that results will be perfect, and so on as far as
infinity.
As we have seen this algorithm is precisely that
given by Euclid
in the Elements. However, it is probable that this methods of generating
perfect numbers was part of the general mathematical tradition handed down from
before Euclid's
time and continuing till Nicomachus
wrote his treatise. Whether the five assertions of Nicomachus
were based on any more than this algorithm and the fact the there were four
perfect numbers known to him 6, 28, 496 and 8128, it is impossible to say, but
it does seem unlikely that anything more lies behind the unproved assertions.
Some of the assertions are made in this quote about perfect numbers which
follows the description of the algorithm [1]:-
... only one is found among the units, 6, only one
other among the tens, 28, and a third in the rank of the hundreds,
496 alone, and a fourth within the limits of the thousands, that is,
below ten thousand, 8128. And it is their accompanying characteristic
to end alternately in 6 or 8, and always to be even.
When these have been discovered, 6 among the units and
28 in the tens, you must do the same to fashion the next. ... the
result is 496, in the hundreds; and then comes 8128 in the
thousands, and so on, as far as it is convenient for one to follow.
Despite the fact that Nicomachus
offered no justification of his assertions, they were taken as fact for many
years. Of course there was the religious significance that we have not mentioned
yet, namely that 6 is the number of days taken by God to create the world, and
it was believed that the number was chosen by him because it was perfect. Again
God chose the next perfect number 28 for the number of days it takes the Moon to
travel round the Earth. Saint Augustine (354-430) writes in his famous text
The City of God :
Six is a number perfect in itself, and not because God
created all things in six days; rather, the converse is true. God created all
things in six days because the number is perfect...
The Arab mathematicians were also fascinated by
perfect numbers and Thabit
ibn Qurra wrote the Treatise on amicable numbers in which he examined
when numbers of the form 2np, where p is prime,
can be perfect. Ibn
al-Haytham proved a partial converse to Euclid's
proposition in the unpublished work Treatise on analysis and synthesis
when he showed that perfect numbers satisfying certain conditions had to be of
the form 2k-1(2k - 1) where
2k - 1 is prime.
Among the many Arab mathematicians to take up the
Greek investigation of perfect numbers with great enthusiasm was Ismail ibn
Ibrahim ibn Fallus (1194-1239) who wrote a treatise based on the Introduction
to arithmetic by Nicomachus.
He accepted Nicomachus's
classification of numbers but the work is purely mathematical, not containing
the moral comments of Nicomachus.
Ibn Fallus gave, in his treatise, a table of ten numbers which were claimed to
be perfect, the first seven are correct and are in fact the first seven perfect
numbers, the remaining three numbers are incorrect.
At the beginning of the renaissance of mathematics
in Europe around 1500 the assertions of Nicomachus
were taken as truths, nothing further being known concerning perfect numbers not
even the work of the Arabs. Some even believed the further unjustified and
incorrect result that 2k-1(2k - 1) is a
perfect number for every odd k. Pacioli
certainly seems to have believed in this fallacy. Charles de Bovelles, a
theologian and philosopher, published a book on perfect numbers in 1509. In it
he claimed that Euclid's
formula 2k-1(2k - 1) gives a perfect number
for all odd integers k, see [10]. Yet, rather remarkably, although
unknown until comparatively recently, progress had been made.
The fifth perfect number has been discovered again
(after the unknown results of the Arabs) and written down in a manuscript dated
1461. It is also in a manuscript which was written by Regiomontanus
during his stay at the University of Vienna, which he left in 1461, see [14]. It
has also been found in a manuscript written around 1458, while both the fifth
and sixth perfect numbers have been found in another manuscript written by the
same author probably shortly after 1460. All that is known of this author is
that he lived in Florence and was a student of Domenico d'Agostino Vaiaio.
In 1536, Hudalrichus Regius made the first
breakthrough which was to become common knowledge to later mathematicians, when
he published Utriusque Arithmetices in which he gave the factorisation
211 - 1 = 2047 = 23 . 89. With this he had found the first prime p
such that 2p-1(2p - 1) is not a perfect
number. He also showed that 213 - 1 = 8191 is prime so he had
discovered (and made his discovery known) the fifth perfect number
212(213 - 1) = 33550336. This showed that Nicomachus's
first assertion is false since the fifth perfect number has 8 digits. Nicomachus's
claim that perfect numbers ended in 6 and 8 alternately still stood however. It
is perhaps surprising that Regius, who must have thought he had made one of the
major breakthroughs in mathematics, is virtually unheard of today.
J Scheybl gave the sixth perfect number in 1555 in
his commentary to a translation of Euclid's
Elements. This was not noticed until 1977 and therefore did not influence
progress on perfect numbers.
The next step forward came in 1603 when Cataldi
found the factors of all numbers up to 800 and also a table of all primes up to
750 (there are 132 such primes). Cataldi
was able use his list of primes to show that 217- 1 = 131071 is prime
(since 7502 = 562500 > 131071 he could check with a tedious
calculation that 131071 had no prime divisors). From this Cataldi
now knew the sixth perfect number, namely 216(217 - 1) =
8589869056. This result by Cataldi
showed that Nicomachus's
assertion that perfect numbers ended in 6 and 8 alternately was false since the
fifth and sixth perfect numbers both ended in 6. Cataldi
also used his list of primes to check that 219 - 1 = 524287 was prime
(again since 7502 = 562500 > 524287) and so he had also found the
seventh perfect number, namely 218(219 - 1) =
137438691328.
As the reader will have already realised, the
history of perfect numbers is littered with errors and Cataldi,
despite having made the major advance of finding two new perfect numbers, also
made some false claims. He writes in Utriusque Arithmetices that the
exponents p = 2, 3, 5, 7, 13, 17, 19, 23, 29, 31, 37 give perfect numbers
2p-1(2p - 1). He is, of course, right for
p = 2, 3, 5, 7, 13, 17, 19 for which he had a proof from his table of
primes, but only one of his further four claims 23, 29, 31, 37 is correct.
Many mathematicians were interested in perfect
numbers and tried to contribute to the theory. For example Descartes,
in a letter to Mersenne
in 1638, wrote :
... I think I am able to prove that there are
no even numbers which are perfect apart from those of Euclid;
and that there are no odd perfect numbers, unless they are composed of a
single prime number, multiplied by a square whose root is composed of several
other prime number. But I can see nothing which would prevent one from finding
numbers of this sort. For example, if 22021 were prime, in multiplying
it by 9018009 which is a square whose root is composed of the prime
numbers 3, 7, 11, 13, one would have 198585576189, which would
be a perfect number. But, whatever method one might use, it would require a
great deal of time to look for these numbers...
The next major contribution was made by Fermat.
He told Roberval
in 1636 that he was working on the topic and, although the problems were very
difficult, he intended to publish a treatise on the topic. The treatise would
never be written, partly because Fermat
never got round to writing his results up properly, but also because he did not
achieve the substantial results on perfect numbers he had hoped. In June 1640
Fermat
wrote to Mersenne
telling him about his discoveries concerning perfect numbers. He wrote:-
... here are three propositions I have discovered, upon
which I hope to erect a great structure. The numbers less by one than the
double progression, like
1 2 3 4 5 6 7 8 9 10 11 12 13
1 3 7 15 31 63 127 255 511 1023 2047 4095 8191 let them be
called the radicals of perfect numbers, since whenever they are prime, they
produce them. Put above these numbers in natural progression 1, 2, 3, 4,
5, etc., which are called their exponents. This done, I say
- When the exponent of a radical number is composite, its radical is
also composite. Just as 6, the exponent of 63, is composite, I
say that 63 will be composite.
- When the exponent is a prime number, I say that its radical less one
is divisible by twice the exponent. Just as 7, the exponent of
127, is prime, I say that 126 is a multiple of 14.
- When the exponent is a prime number, I say that its radical cannot be
divisible by any other prime except those that are greater by one than a
multiple of double the exponent...
Here are three
beautiful propositions which I have found and proved without difficulty, I
shall call them the foundations of the invention of perfect numbers. I don't
doubt that Frenicle
de Bessy got there earlier, but I have only begun and without doubt
these propositions will pass as very lovely in the minds of those who have not
become sufficiently hypocritical of these matters, and I would be very happy
to have the opinion of M Roberval.
Shortly after writing this letter to Mersenne,
Fermat
wrote to Frenicle
de Bessy on 18 October 1640. In this letter he gave a generalisation of
results in the earlier letter stating the result now known as Fermat's
Little Theorem which shows that for any prime p and an integer a
not divisible by p, ap-1- 1 is divisible by
p. Certainly Fermat
found his Little Theorem as a consequence of his investigations into perfect
numbers.
Using special cases of his Little Theorem, Fermat
was able to disprove two of Cataldi's
claims in his June 1640 letter to Mersenne.
He showed that 223 - 1 was composite (in fact 223 - 1 = 47
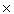 178481) and that
237 - 1 was composite (in fact 237 - 1 = 223 178481) and that
237 - 1 was composite (in fact 237 - 1 = 223 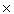 616318177). Frenicle
de Bessy had, earlier in that year, asked Fermat
(in correspondence through Mersenne)
if there was a perfect number between 1020 and 1022. In
fact assuming that perfect numbers are of the form
2p-1(2p - 1) where p is prime, the
question readily translates into asking whether 237 - 1 is prime. Fermat
not only states that 237 - 1 is composite in his June 1640 letter,
but he tells Mersenne
how he factorised it. 616318177). Frenicle
de Bessy had, earlier in that year, asked Fermat
(in correspondence through Mersenne)
if there was a perfect number between 1020 and 1022. In
fact assuming that perfect numbers are of the form
2p-1(2p - 1) where p is prime, the
question readily translates into asking whether 237 - 1 is prime. Fermat
not only states that 237 - 1 is composite in his June 1640 letter,
but he tells Mersenne
how he factorised it.
Fermat
used three theorems:-
(i) If n is composite, then 2n - 1
is composite.
(ii) If n is prime, then 2n - 2
is a multiple of 2n.
(iii) If n is prime, p a
prime divisor of 2n- 1, then p - 1 is a multiple of
n.
Note that (i) is trivial while (ii) and (iii) are
special cases of Fermat's
Little Theorem. Fermat
proceeds as follows: If p is a prime divisor of 237 - 1, then
37 divides p - 1. As p is odd, it is a prime of the form 2 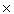 37m+1, for some m.
The first case to try is p = 149 and this fails (a test division is
carried out). The next case to try is 223 (the case m = 3) which succeeds
and 237 - 1 = 223 37m+1, for some m.
The first case to try is p = 149 and this fails (a test division is
carried out). The next case to try is 223 (the case m = 3) which succeeds
and 237 - 1 = 223 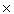 616318177. 616318177.
Mersenne
was very interested in the results that Fermat
sent him on perfect numbers and soon produced a claim of his own which was to
fascinate mathematicians for a great many years. In 1644 he published
Cogitata physica mathematica in which he claimed that
2p - 1 is prime (and so
2p-1(2p - 1) is a perfect number)
for
p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257
and for no other
value of p up to 257. Now certainly Mersenne
could not have checked these results and he admitted this himself saying:-
... to tell if a given number of 15 or 20
digits is prime, or not, all time would not suffice for the
test.
The remarkable fact is that Mersenne
did very well if this was no more than a guess. There are 47 primes p
greater than 19 yet less than 258 for which 2p - 1 might have
been either prime or composite. Mersenne
got 42 right and made 5 mistakes.
Primes of the form 2p- 1 are called Mersenne
primes.
The next person to make a major contribution to
the question of perfect numbers was Euler.
In 1732 he proved that the eighth perfect number was
230(231 - 1) = 2305843008139952128. It was the first new
perfect number discovered for 125 years. Then in 1738 Euler
settled the last of Cataldi's
claims when he proved that 229 - 1 was not prime (so Cataldi's
guesses had not been very good). Now it should be noticed (as it was at the
time) that Mersenne
had been right on both counts, since p = 31 appears in his list but p = 29 does not.
In two manuscripts which were unpublished during
his life, Euler
proved the converse of Euclid's
result by showing that every even perfect number had to be of the form
2p-1(2p - 1). This verifies the fourth assertion of Nicomachus
at least in the case of even numbers. It also leads to an easy proof that all
even perfect numbers end in either a 6 or 8 (but not alternately). Euler
also tried to make some headway on the problem of whether odd perfect numbers
existed. He was able to prove the assertion made by Descartes
in his letter to Mersenne
in 1638 from which we quoted above. He went a little further and proved that any
odd perfect number had to have the form
(4n+1)4k+1 b2
where 4n+1 is prime. However, as with most others whose
contribution we have examined, Euler
made predictions about perfect numbers which turned out to be wrong. He claimed
that 2p-1(2p - 1) was perfect for p =
41 and p = 47 but Euler
does have the distinction of finding his own error, which he corrected in 1753.
The search for perfect numbers had now become an
attempt to check whether Mersenne
was right with his claims in Cogitata physica mathematica. In fact
Euler's
results had made many people believe that Mersenne
had some undisclosed method which would tell him the correct answer. In fact
Euler's
perfect number 230(231 - 1) remained the largest known for
over 150 years. Mathematicians such as Peter Barlow
wrote in his book Theory of Numbers published in 1811, that the perfect
number 230(231 - 1):-
... is the greatest that ever will be discovered; for as
they are merely curious, without being useful, it is not likely that any
person will ever attempt to find one beyond it.
This, of course, turned out to be yet one more false assertion about perfect numbers!
The first error in Mersenne's
list was discovered in 1876 by Lucas.
He was able to show that 267 - 1 is not a prime although his methods
did not allow him to find any factors of it. Lucas
was also able to verify that one of the numbers in Mersenne's
list was correct when he showed that 2127 - 1 is a Mersenne
prime and so 2126(2127- 1) is indeed a perfect number. Lucas
made another important advance which, as modified by Lehmer in 1930, is the
basis of computer searches used today to find Mersenne
primes, and so to find perfect numbers. Following the announcement by Lucas
that p = 127 gave the Mersenne
prime 2p - 1, Catalan
conjectured that, if m = 2p - 1 is prime then
2m - 1 is also prime. This Catalan
sequence is 2p - 1 where
p = 3, 7, 127, 170141183460469231731687303715884105727,
...
Of course if this conjecture were true it would
solve the still open question of whether there are an infinite number of Mersenne
primes (and also solve the still open question of whether there are infinitely
many perfect numbers). However checking whether the fourth term of this
sequence, namely 2p - 1 for p =
170141183460469231731687303715884105727, is prime is well beyond what is
possible.
In 1883 Pervusin showed that
260(261- 1) is a perfect number. This was shown
independently three years later by Seelhoff. Many mathematicians leapt to defend
Mersenne
saying that the number 67 in his list was a misprint for 61.
In 1903 Cole
managed to factorise 267 - 1, the number shown to be composite by Lucas,
but for which no factors were known up to that time. In October 1903 Cole
presented a paper On the factorisation of large numbers to a meeting of
the American Mathematical Society. In one of the strangest 'talks' ever given,
Cole
wrote on the blackboard
267 - 1 = 147573952589676412927.
Then he wrote 761838257287 and underneath it 193707721. Without
speaking a work he multiplied the two numbers together to get
147573952589676412927 and sat down to applause from the audience. [It is worth
remarking that the computer into which I [EFR] am typing this article gave this
factorisation of 267 - 1 in about a second - times have changed!]
Further mistakes made by
Mersenne
were found. In 1911 Powers showed that 288
(289 - 1)
was a perfect number, then a few years later he showed that 2101- 1
is a prime and so 2100(2101- 1) is a perfect number. In
1922 Kraitchik showed that Mersenne
was wrong in his claims for his largest prime of 257 when he showed that
2257- 1 is not prime.
We have followed the progress of finding even
perfect numbers but there was also attempts to show that an odd perfect number
could not exist. The main thrust of progress here has been to show the minimum
number of distinct prime factors that an odd perfect number must have.
Sylvester worked on this problem and wrote (see [20]):-
... the existence of [an odd perfect number] -
its escape, so to say, from the complex web of conditions which hem it in on
all sides - would be little short of a miracle.
Sylvester proved in 1888 that any odd perfect number must have at least 4 distinct prime
factors. Later in the same year he improved his result to five factors and, over
the years, this has been steadily improved until today we know that an odd
perfect number would have to have at least eight distinct prime factors, and at
least 29 prime factors which are not necessarily distinct. It is also known that
such a number would have more than 300 digits and a prime divisor greater than
106. The problem of whether an odd perfect number exists, however,
remains unsolved.
Today 39 perfect numbers are known,
288(289- 1) being the last to be discovered by hand
calculations in 1911 (although not the largest found by hand calculations), all
others being found using a computer. In fact computers have led to a revival of
interest in the discovery of
Mersenne
primes, and therefore of perfect numbers. At the moment the largest known
Mersenne
prime is 213466917 - 1 (which is also the largest known prime) and
the corresponding largest known perfect number is
213466916(213466917 - 1). It was discovered in December
2001 and this, the 39th such prime to be discovered, contains more than 4
million digits. If you wonder why we haven't included the number in decimal
form, then let me say that it contains about 150 times as many characters as
this whole article on perfect numbers. Also worth noting is the fact that
although this is the 39th to be discovered, it may not be the 39th perfect
number as not all smaller cases have been ruled out.
The number Pi
A little known verse of the Bible reads
And he made a molten sea, ten cubits from the one brim to
the other: it was round all about, and his height was five cubits: and a line
of thirty cubits did compass it about. (I Kings 7, 23)
The same verse can be found in II Chronicles 4, 2. It occurs in
a list of specifications for the great temple of Solomon, built around 950 BC
and its interest here is that it gives p = 3. Not a
very accurate value of course and not even very accurate in its day, for the
Egyptian and Mesopotamian values of 25/8 = 3.125
and 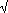 10 = 3.162 have been traced to
much earlier dates: though in defence of Solomon's craftsmen it should be noted
that the item being described seems to have been a very large brass casting,
where a high degree of geometrical precision is neither possible nor necessary.
There are some interpretations of this which lead to a much better
value. 10 = 3.162 have been traced to
much earlier dates: though in defence of Solomon's craftsmen it should be noted
that the item being described seems to have been a very large brass casting,
where a high degree of geometrical precision is neither possible nor necessary.
There are some interpretations of this which lead to a much better
value.
The fact that the ratio of the circumference to the diameter of
a circle is constant has been known for so long that it is quite untraceable.
The earliest values of p including the 'Biblical' value
of 3, were almost certainly found by measurement. In the Egyptian Rhind Papyrus, which is dated about 1650 BC, there is good
evidence for 4(8/9)2 = 3.16 as a value for
p.
The first theoretical calculation seems to have been
carried out by Archimedes
of Syracuse (287-212 BC). He obtained the approximation
223/71 < p
< 22/7.
Before giving an indication of his proof, notice
that very considerable sophistication involved in the use of inequalities here.
Archimedes
knew, what so many people to this day do not, that p
does not equal 22/7, and made no claim to have discovered
the exact value. If we take his best estimate as the average of his two bounds
we obtain 3.1418, an error of about 0.0002.p
Here is Archimedes'
argument.
Consider a circle of radius 1, in which we inscribe a regular
polygon of 3 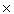 2n-1 sides, with semiperimeter bn,
and superscribe a regular polygon of 3
2n-1 sides, with semiperimeter bn,
and superscribe a regular polygon of 3 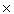 2n-1 sides, with
semiperimeter an. 2n-1 sides, with
semiperimeter an.

The diagram for the case n = 2 is on the right.
The effect of this procedure is to define an increasing
sequence
b1, b2,
b3, ...
and a decreasing sequence
a1, a2,
a3, ...
such that both sequences have limit p.
Using trigonometrical notation, we see that the two
semiperimeters are given by
an = K tan(p/K), bn = K
sin(p/K),
where K = 3 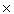 2n-1. Equally, we have 2n-1. Equally, we have
an+1 = 2K tan(p/2K), bn+1 =
2K sin(p/2K),
and it is not a difficult exercise in trigonometry to show that
(1) . . . (1/an +
1/bn) = 2/an+1
(2) . . .
an+1bn =
(bn+1)2.
Archimedes,
starting from a1 = 3 tan(p/3)
= 3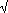 3 and b1 = 3
sin(p/3) = 3 3 and b1 = 3
sin(p/3) = 3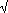 3/2, calculated a2 using (1),
then b2 using (2), then a3 using (1), then
b3 using (2), and so on until he had calculated
a6 and b6. His conclusion was that 3/2, calculated a2 using (1),
then b2 using (2), then a3 using (1), then
b3 using (2), and so on until he had calculated
a6 and b6. His conclusion was that
b6 < p
< a6.
It is important to realise that the use of
trigonometry here is unhistorical: Archimedes
did not have the advantage of an algebraic and trigonometrical notation and had
to derive (1) and (2) by purely geometrical means. Moreover he did not even have
the advantage of our decimal notation for numbers, so that the calculation of
a6 and b6 from (1) and (2) was by no means a
trivial task. So it was a pretty stupendous feat both of imagination and of
calculation and the wonder is not that he stopped with polygons of 96 sides, but
that he went so far.
For of course there is no reason in principle why one should
not go on. Various people did, including:
Except for Zu
Chongzhi, about whom next to nothing is known and who is very unlikely to
have known about Archimedes'
work, there was no theoretical progress involved in these improvements, only
greater stamina in calculation. Notice how the lead, in this as in all
scientific matters, passed from Europe to the East for the millennium 400 to
1400 AD.
Al-Khwarizmi
lived in Baghdad, and incidentally gave his name to 'algorithm', while the words
al jabr in the title of one of his books gave us the word 'algebra'. Al-Kashi
lived still further east, in Samarkand, while Zu
Chongzhi, one need hardly add, lived in China.
The European Renaissance brought about in due course
a whole new mathematical world. Among the first effects of this reawakening was
the emergence of mathematical formulae for p. One of
the earliest was that of Wallis
(1616-1703)
2/p = (1.3.3.5.5.7....)/(2.2.4.4.6.6. ...)
and one of the best-known is
p/4 = 1 -
1/3 + 1/5 -
1/7 + ....
This formula is sometimes attributed to
Leibniz
(1646-1716) but is seems to have been first discovered by James Gregory
(1638- 1675).
These are both dramatic and astonishing formulae, for the
expressions on the right are completely arithmetical in character, while p arises in the first instance from geometry. They show the
surprising results that infinite processes can achieve and point the way to the
wonderful richness of modern mathematics.
From the point of view of the calculation of p, however, neither is of any use at all. In
Gregory's
series, for example, to get 4 decimal places correct we require the error to be
less than 0.00005 = 1/20000, and so we need about 10000
terms of the series. However, Gregory
also showed the more general result
(3) . . . tan-1 x = x -
x3/3 + x5/5 - ... (-1 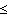 x x 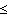 1) 1)
from which the first series results if we put x = 1. So
using the fact that
tan-1(1/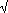 3) = p/6 we get 3) = p/6 we get
p/6 =
(1/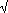 3)(1 -
1/(3.3) + 1/(5.3.3) - 1/(7.3.3.3) + ... 3)(1 -
1/(3.3) + 1/(5.3.3) - 1/(7.3.3.3) + ...
which converges much more quickly. The 10th term is
1/19 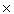 39
39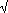 3, which is less than
0.00005, and so we have at least 4 places correct after just 9 terms. 3, which is less than
0.00005, and so we have at least 4 places correct after just 9 terms.
An even better idea is to take the formula
(4) . . . p/4 =
tan-1(1/2) +
tan-1(1/3)
and then calculate the two series obtained by putting first
1/2 and the 1/3 into (3).
Clearly we shall get very rapid convergence indeed if we can
find a formula something like
p/4 =
tan-1(1/a) +
tan-1(1/b)
with a and b large. In 1706 Machin
found such a formula:
(5) . . . p/4 = 4
tan-1(1/5) -
tan-1(1/239)
Actually this is not at all hard to prove, if you know how to
prove (4) then there is no real extra difficulty about (5), except that the
arithmetic is worse. Thinking it up in the first place is, of course, quite
another matter.
With a formula like this available the only
difficulty in computing p is the sheer boredom of
continuing the calculation. Needless to say, a few people were silly enough to
devote vast amounts of time and effort to this tedious and wholly useless
pursuit. One of them, an Englishman named Shanks,
used Machin's
formula to calculate p to 707 places, publishing the
results of many years of labour in 1873. Shanks has achieved immortality for a
very curious reason which we shall explain in a moment.
Here is a summary of
how the improvement went:
| 1699:
| Sharp used Gregory's
result to get 71 correct digits
|
| 1701:
| Machin used an improvement to get 100 digits and the following used
his methods:
|
| 1719:
| de Lagny
found 112 correct digits
|
| 1789:
| Vega got 126 places and in 1794 got 136
|
| 1841:
| Rutherford calculated 152 digits and in 1853 got 440
|
| 1873:
| Shanks
calculated 707 places of which 527 were
correct
|
A more detailed Chronology is available.
Shanks
knew that p was irrational since this had been proved
in 1761 by Lambert.
Shortly after Shanks'
calculation it was shown by Lindemann
that p is transcendental, that is, p is not the solution of any polynomial equation with integer
coefficients. In fact this result of Lindemann
showed that 'squaring the circle' is impossible. The transcendentality of p implies that there is no ruler and compass construction to
construct a square equal in area to a given circle.
Very soon after Shanks'
calculation a curious statistical freak was noticed by De
Morgan, who found that in the last of 707 digits there was a suspicious
shortage of 7's. He mentions this in his Budget of Paradoxes of 1872 and
a curiosity it remained until 1945 when Ferguson discovered that Shanks
had made an error in the 528th place, after which all his digits were
wrong. In 1949 a computer was used to calculate p to
2000 places. In this and all subsequent computer expansions the number of 7's
does not differ significantly from its expectation, and indeed the sequence of
digits has so far passed all statistical tests for randomness.
You can see 2000 places of p.
We should say a little of how the notation p arose. Oughtred
in 1647 used the symbol d/p for the ratio
of the diameter of a circle to its circumference. David
Gregory (1697) used p/r for the ratio
of the circumference of a circle to its radius. The first to use p with its present meaning was an Welsh mathematician
William Jones
in 1706 when he states 3.14159 andc. = p. Euler
adopted the symbol in 1737 and it quickly became a standard notation.
We conclude with one further statistical curiosity
about the calculation of p, namely Buffon's
needle experiment. If we have a uniform grid of parallel lines, unit distance
apart and if we drop a needle of length k < 1 on the grid, the probability
that the needle falls across a line is 2k/p. Various people have tried to calculate p by throwing needles. The most remarkable result was that of
Lazzerini (1901), who made 34080 tosses and got
p = 355/113 =
3.1415929
which, incidentally, is the value found by Zu
Chongzhi. This outcome is suspiciously good, and the game is given away by
the strange number 34080 of tosses. Kendall and Moran comment that a good value
can be obtained by stopping the experiment at an optimal moment. If you set in
advance how many throws there are to be then this is a very inaccurate way of
computing p. Kendall and Moran comment that you would
do better to cut out a large circle of wood and use a tape measure to find its
circumference and diameter.
Still on the theme of phoney experiments, Gridgeman, in a paper
which pours scorn on Lazzerini and others, created some amusement by using a
needle of carefully chosen length k = 0.7857, throwing it twice, and hitting a
line once. His estimate for p was thus given by
2 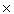 0.7857 /
p = 1/2 0.7857 /
p = 1/2
from which he got the highly creditable value of p = 3.1428. He was not being serious!
It is almost unbelievable that a definition of
p was used, at least as an excuse, for a racial attack
on the eminent mathematician Edmund Landau
in 1934. Landau
had defined p in this textbook published in Göttingen
in that year by the, now fairly usual, method of saying that p/2 is the value of x between 1 and 2 for which
cos x vanishes. This unleashed an academic dispute which was to end in Landau's
dismissal from his chair at Göttingen. Bieberbach,
an eminent number theorist who disgraced himself by his racist views, explains
the reasons for Landau's
dismissal:-
Thus the valiant rejection by the Göttingen
student body which a great mathematician, Edmund Landau,
has experienced is due in the final analysis to the fact that the un-German
style of this man in his research and teaching is unbearable to German
feelings. A people who have perceived how members of another race are working
to impose ideas foreign to its own must refuse teachers of an alien culture.
G H Hardy
replied immediately to Bieberbach
in a published note about the consequences of this un-German definition of p
There are many of us, many Englishmen and
many Germans, who said things during the War which we scarcely meant and are
sorry to remember now. Anxiety for one's own position, dread of falling behind
the rising torrent of folly, determination at all cost not to be outdone, may
be natural if not particularly heroic excuses. Professor Bieberbach's
reputation excludes such explanations of his utterances, and I find myself
driven to the more uncharitable conclusion that he really believes them true.
Not only in Germany did p present
problems. In the USA the value of p gave rise to heated
political debate. In the State of Indiana in 1897 the House of Representatives
unanimously passed a Bill introducing a new mathematical truth.
Be it enacted by the General Assembly of the State of
Indiana: It has been found that a circular area is to the square on a line
equal to the quadrant of the circumference, as the area of an equilateral
rectangle is to the square of one side.
(Section I, House Bill No. 246,
1897)
The Senate of Indiana showed a little more sense and postponed
indefinitely the adoption of the Act!
Open questions about the number p
- Does each of the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 each occur infinitely
often in p?
- Brouwer's
question: In the decimal expansion of p, is there a
place where a thousand consecutive digits are all zero?
- Is p simply normal to base 10? That is does every
digit appear equally often in its decimal expansion in an asymptotic sense?
- Is p normal to base 10? That is does every block
of digits of a given length appear equally often in its decimal expansion in
an asymptotic sense?
- Is p normal ? That is does every block of
digits of a given length appear equally often in the expansion in every base
in an asymptotic sense? The concept was introduced by Borel
in 1909.
- Another normal question! We know that p is not
rational so there is no point from which the digits will repeat. However, if
p is normal then the first million digits
314159265358979... will occur from some point. Even if p is not normal this might hold! Does it? If so from what
point? Note: Up to 200 million the longest to appear is 31415926 and this
appears twice.
As a postscript, here is a mnemonic for the decimal expansion
of p. Each successive digit is the number of letters in
the corresponding word.
How I want a drink, alcoholic of course, after
the heavy lectures involving quantum mechanics. All of thy geometry, Herr
Planck,
is fairly hard...:
3.14159265358979323846264...
The number Phi
The number Phi is an approximation of the Fibonacci sequence,
the higher one goes in the Fibonacci Sequence the closer ones gets to the Golden Ratio.
|
In this series of numbers each term is the sum of the
previous two terms as follows: |
| 1 1 2 3 5 8 13 21 34 55 89 144 233 377 . . . |
8 / 5 = 1.6
13 / 8 = 1.625
21 / 13 = 1.615
...
233 / 144 = 1.618
The division of any two adjacent numbers gives the amazing
Golden number : 1.618.
The Golden Ratio can be expressed as 1.618 and 0.618 and is known
as Phi and phi, respectively; phi being the reciprocal of
Phi... This is a very unique property that only the Golden Ratio
possesses:
1 / Phi = phi
(1 / 1.618 = 0.618)
and...
1 / phi = Phi (1 / 0.618 = 1.618)
Also, Phi Squared = Phi + 1
(1.618 ^2 = 1.618 + 1)
...and Phi multiplied by phi = 1
(1.618 * 0.618 = 1)
Phi is not a fraction: In other words, there is no
way to express Phi as using two integers, e.g. (2/3)
Deriving Phi:
Phi = Square root of 5 + 1 / 2...
or (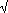 5+1)/2
Phi to 31 decimal places:
1.6180339887498948482045868343656 5+1)/2
Phi to 31 decimal places:
1.6180339887498948482045868343656
The number e
One of the first articles which we included in the "History
Topics" section of our web archive was on the history of p. It is a very popular article and has prompted many to ask
for a similar article about the number e. There is a great contrast
between the historical developments of these two numbers and in many ways
writing a history of e is a much harder task than writing one for p. The number e is, compared to p, a relative newcomer on the mathematics scene.
The number e first comes into mathematics
in a very minor way. This was in 1618 when, in an appendix to Napier's
work on logarithms, a table appeared giving the natural logarithms of various
numbers. However, that these were logarithms to base e was not recognised
since the base to which logarithms are computed did not arise in the way that
logarithms were thought about at this time. Although we now think of logarithms
as the exponents to which one must raise the base to get the required number,
this is a modern way of thinking. We will come back to this point later in this
essay. This table in the appendix, although carrying no author's name, was
almost certainly written by Oughtred.
A few years later, in 1624, again e almost made it into the mathematical
literature, but not quite. In that year Briggs
gave a numerical approximation to the base 10 logarithm of e but did not
mention e itself in his work.
The next possible occurrence of e is
again dubious. In 1647 Saint-Vincent
computed the area under a rectangular hyperbola. Whether he recognised the
connection with logarithms is open to debate, and even if he did there was
little reason for him to come across the number e explicitly. Certainly
by 1661 Huygens
understood the relation between the rectangular hyperbola and the logarithm. He
examined explicitly the relation between the area under the rectangular
hyperbola yx = 1 and the logarithm. Of course, the number e is
such that the area under the rectangular hyperbola from 1 to e is equal
to 1. This is the property that makes e the base of natural logarithms,
but this was not understood by mathematicians at this time, although they were
slowly approaching such an understanding.
Huygens
made another advance in 1661. He defined a curve which he calls "logarithmic"
but in our terminology we would refer to it as an exponential curve, having the
form y = kax. Again out of this comes the
logarithm to base 10 of e, which Huygens
calculated to 17 decimal places. However, it appears as the calculation of a
constant in his work and is not recognised as the logarithm of a number (so
again it is a close call but e remains unrecognised).
Further work on logarithms followed which still
does not see the number e appear as such, but the work does contribute to
the development of logarithms. In 1668 Nicolaus
Mercator published Logarithmotechnia which contains the series
expansion of log(1+x). In this work Mercator uses the term "natural
logarithm" for the first time for logarithms to base e. The number
e itself again fails to appear as such and again remains elusively just
round the corner.
Perhaps surprisingly, since this work on
logarithms had come so close to recognising the number e, when e
is first "discovered" it is not through the notion of logarithm at all but
rather through a study of compound interest. In 1683 Jacob
Bernoulli looked at the problem of compound interest and, in examining
continuous compound interest, he tried to find the limit of (1 +
1/n)n as n tends to infinity. He used
the binomial theorem to show that the limit had to lie between 2 and 3 so we
could consider this to be the first approximation found to e. Also if we
accept this as a definition of e, it is the first time that a number was
defined by a limiting process. He certainly did not recognise any connection
between his work and that on logarithms.
We mentioned above that logarithms were not
thought of in the early years of their development as having any connection with
exponents. Of course from the equation x = at,
we deduce that t = log x where the log is to base a, but
this involves a much later way of thinking. Here we are really thinking of log
as a function, while early workers in logarithms thought purely of the log as a
number which aided calculation. It may have been Jacob
Bernoulli who first understood the way that the log function is the inverse
of the exponential function. On the other hand the first person to make the
connection between logarithms and exponents may well have been James
Gregory. In 1684 he certainly recognised the connection between logarithms
and exponents, but he may not have been the first.
As far as we know the first time the number
e appears in its own right is in 1690. In that year Leibniz
wrote a letter to Huygens
and in this he used the notation b for what we now call e. At last
the number e had a name (even if not its present one) and it was
recognised. Now the reader might ask, not unreasonably, why we have not started
our article on the history of e at the point where it makes its first
appearance. The reason is that although the work we have described previously
never quite managed to identify e, once the number was identified then it
was slowly realised that this earlier work is relevant. Retrospectively, the
early developments on the logarithm became part of an understanding of the
number e.
We mentioned above the problems arising from
the fact that log was not thought of as a function. It would be fair to say that
Johann
Bernoulli began the study of the calculus of the exponential function in
1697 when he published Principia calculi exponentialum seu percurrentium.
The work involves the calculation of various exponential series and many results
are achieved with term by term integration.
So much of our mathematical notation is due to
Euler
that it will come as no surprise to find that the notation e for this
number is due to him. The claim which has sometimes been made, however, that Euler
used the letter e because it was the first letter of his name is
ridiculous. It is probably not even the case that the e comes from
"exponential", but it may have just be the next vowel after "a" and Euler
was already using the notation "a" in his work. Whatever the reason, the
notation e made its first appearance in a letter Euler
wrote to Goldbach
in 1731. He made various discoveries regarding e in the following years,
but it was not until 1748 when Euler
published Introductio in Analysin infinitorum that he gave a full
treatment of the ideas surrounding e. He showed that
e = 1 + 1/1! + 1/2! + 1/3! + ...
and that e is the limit of (1 +
1/n)n as n tends to
infinity. Euler
gave an approximation for e to 18 decimal places,
e = 2.718281828459045235
without saying where this came from. It is
likely that he calculated the value himself, but if so there is no indication of
how this was done. In fact taking about 20 terms of 1 + 1/1! + 1/2! + 1/3! + ... will give the accuracy which Euler
gave. Among other interesting results in this work is the connection between the
sine and cosine functions and the complex exponential function, which Euler
deduced using De
Moivre's formula.
Interestingly Euler
also gave the continued fraction expansion of e and noted a pattern in
the expansion. In particular he gave
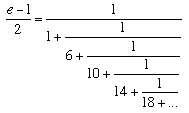
and
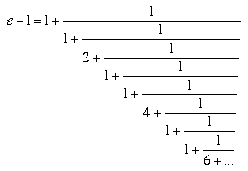
Euler
did not give a proof that the patterns he spotted continue (which they do) but
he knew that if such a proof were given it would prove that e is
irrational. For, if the continued fraction for (e - 1)/2 were to follow
the pattern shown in the first few terms, 6, 10, 14, 18, 22, 26, ... (add 4 each
time) then it will never terminate so (e - 1)/2 (and so e) cannot
be rational. One could certainly see this as the first attempt to prove that
e is not rational.
The same passion that drove people to calculate
to more and more decimal places of p never seemed to
take hold in quite the same way for e. There were those who did calculate
its decimal expansion, however, and the first to give e to a large number
of decimal places was Shanks
in 1854. It is worth noting that Shanks
was an even more enthusiastic calculator of the decimal expansion of p. Glaisher
showed that the first 137 places of Shanks
calculations for e were correct but found an error which, after
correction by Shanks,
gave e to 205 places. In fact one needs about 120 terms of 1 +
1/1! + 1/2! + 1/3! + ... to obtain e correct to
200 places.
In 1864 Benjamin
Peirce had his picture taken standing in front of a blackboard on which he
had written the formula i-i = 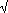 (ep). In his lectures he would say to his students:- (ep). In his lectures he would say to his students:-
Gentlemen, we have not the slightest idea what this
equation means, but we may be sure that it means something very important.
Most people accept Euler
as the first to prove that e is irrational. Certainly it was Hermite
who proved that e is not an algebraic number in 1873. It is still an open
question whether ee is algebraic, although of course
all that is lacking is a proof - no mathematician would seriously believe that
ee is algebraic! As far as we are aware, the closest
that mathematicians have come to proving this is a recent result that at least
one of ee and e to the power
e2 is transcendental.
Further calculations of decimal expansions
followed. In 1884 Boorman calculated e to 346 places and found that his
calculation agreed with that of Shanks
as far as place 187 but then became different. In 1887 Adams calculated the
logarithm of e to the base 10 to 272 places.
| 

