I Numeri Primi

I numeri primi sono gioielli incastonati nell'immensa distesa dei numeri, l'universo infinito che i matematici esplorano da secoli. Ai matematici i numeri primi infondono un senso di meraviglia: 2, 3, 5, 7,11, 13, 17,19, 23..., numeri senza tempo che esistono in un mondo indipendente dalla nostra realtà fisica. Sono un dono che la Natura ha fatto al matematico.

Quella che segue è la tabella dei numeri primi inferiori a 1000

La loro importanza per la matematica deriva dal fatto che hanno il potere di costruire tutti gli altri numeri. Ogni numero intero che non sia primo può essere costruito moltiplicando questi elementi di base primari. Ogni molecola esistente nel mondo fisico può essere costruita utilizzando gli atomi della tavola periodica degli elementi chimici. Padroneggiare questi elementi di base offre al matematico la speranza di poter scoprire nuovi metodi per costruire la mappa di un percorso che attraversi le smisurate complessità del mondo matematico.

Eppure, a dispetto della loro apparente semplicità e della loro natura fondamentale, i numeri primi restano gli oggetti più misteriosi studiati dai matematici. In una disciplina che si dedica a trovare andamenti regolari e ordine, i numeri primi presentano la sfida estrema. Provate a esaminare un elenco dì numeri primi. Scoprirete che è impossibile prevedere quando apparirà il successivo. L'elenco sembra caotico, casuale, e non fornisce alcun indizio riguardo al modo dì determinare il suo prossimo elemento.

Riuscite a trovare una formula che generi i numeri dì questo elenco, una regola magica che vi dica qual è il centesimo numero primo? Questo problema affligge la mente dei matematici da molti secoli. Nonostante più di duemila anni dì sforzi, i numeri primi sembrano vanificare ogni tentativo di inserirli in un semplice schema regolare.

Si può sempre sperare che, dopo un inizio nervoso, il battito dei numeri primi si regolarizzi. Non è così: più si prosegue a contare, più le cose peggiorano. Consideriamo, per esempio, ì numeri primi compresi nell'intervallo dei cento numeri che precedono 10.000.000 e nell'intervallo dei cennto numeri che seguono 10.000.000. Cominciamo dai numeri primi inferiori a 10.000.000:

9.999.901,9.999.907,9.999.929,9.999.931,9.999.937, 9.999.943,9.999.971,9.999.973,9.999.991

Ma osservate adesso quanto pochi siano i numeri primi compresi fra 10.000.000 e 10.000.100:

10.000.019, 10.000.079

E difficile pensare a una formula in grado di generare una sequenza di questo tipo. In effetti, questa serie di numeri primi ricorda molto più una successione casuale di numeri che non una struttura ben ordinata.

Il crivello di Eratostene

Eratostene di Girene (l'odierna cittadina di Shahhat in Libia) era uno dei bibliotecari della monumentale Biblioteca di Alessandria. Intorno al 230 a. C., circa settant'anni dopo Euclìde, sviluppò il famoso metodo del crivello, ovvero del setaccio, per determinare i numeri primi.

Funziona in questa maniera. In primo luogo, si scrivono tutti i numeri interi, a partire da 2. Naturalmente, non possiamo scriverli tutti, e dunque li scriviamo fino a 100 all'incirca.

Ora, a partire da 2 e lasciandolo invariato, setacciamo via un numero ogni due. Si ottiene come risultato

Il numero successivo che non è stato eliminato è 3; a partire da questo setacciamo dall'elenco un numero ogni tre, se non è,già stato depennato. Si ottiene

Il primo numero che non è stato eliminato dopo 3 è 5; a partire da questo, depenniamo un numero ogni cinque. Si ottiene

Il primo numero che si salva dopo 5 è 7. Il passo successivo sarebbe partire da 7 e depennare un numero ogni sette, se non è già stato cancellato. Il primo numero che si salva dopo 7 sarebbe allora 11 e così via.

Se continuiamo il procedimento in maniera sistematica, rimangono solo i numeri primi. Questo è il crivello di Eratostene.

Numeri primi gemelli

Con la congettura dei numeri primi gemelli, ci si chiede se esistano infiniti numeri primip tali che p + 2 sia anch'esso un numero primo. Una coppia di numeri primi gemelli è formata da 1.000.037 e 1.000.039. Questa è la minima distanza possìbile fra due numeri primi, dato che N e N + 1 non possono essere entrambi primi — tranne quando N = 2 - poiché almeno uno di essi è divisibile per 2.

Euclide dimostrò duemila anni fa che esìstono infiniti numeri primi, ma nessuno sa se esiste un numero oltre il quale non ci sono più queste coppie di primi ravvicinati. Si ritiene che esistano infiniti primi gemelli. Ma se le supposizioni sono una cosa, la dimostrazione rimane il traguardo finale.

Numeri primi di Mersenne

Fermat portò alla luce alcune delle proprietà molto speciali che i numeri primi possiedono. Egli scoprì un fatto curioso relativo a quei numeri primi che - come 5, 13, 17 e 29 — divisi per 4 danno resto 1. Tali numeri primi possono sempre essere scritti come somma di due quadrati. Per esempio, 29 — 22 + 52. Questa è un'altra delle beffe di Fermat. Sebbene sostenesse di possederne la dimostrazione, mancò dì mettere per iscritto la gran parte dei dettagli.

Il giorno di Natale del 1640, Fermat scrisse della sua scoperta - che era possibile esprimere certi numeri primi come somma di due quadrati — in una lettera inviata a un monaco francese di nome Marin Mersenne. Gli interessi dì Mersenne non si limitavano alle questioni liturgiche. Egli amava la musica e fu il primo a elaborare una teoria coerente degli armonici. Amava anche i numeri. Mersenne e Fermat tenevano una corrispondenza regolare sulle loro scoperte matematiche. Mersenne divenne famoso per il suo ruolo dì intermediario nella comunità scientifica internazionale del Seicento: attraverso di lui, i matematici potevano diffondere le loro idee.

Come era accaduto a intere generazioni di matematici, anche Mersenne fu preso dalla smania di scoprire un ordine nei numeri primi. E anche se non riuscì a trovare una formula che producesse tutti i primi, ne escogitò una che a lungo andare si è dimostrata molto più efficace per scoprire numeri primi di quanto non lo sia la formula di Fermat.

Anch'eglì, come Fermat, partì prendendo in considerazione le potenze di 2, Ma invece di aggiungere 1 al risultato come aveva fatto Fermat, Mersenne decise di sottrarre 1. Per esempio, 2³ — 1 = 8 — 1 = 7) che è un numero primo. Forse gli fu d'aiuto l'intuito musicale. Raddoppiando la frequenza di una nota la si eleva di un'ottava, e dunque le potenze di 2 producono note armoniche. D'altra parte è naturale aspettarsi che uno spostamento di frequenza pari a 1 dia luogo a una nota molto dissonante, incompatibile con tutte le frequenze che la precedono, una «nota prima».

Mersenne scoprì rapidamente che la sua formula non avrebbe dato sempre un numero primo. Per esempio, 2⁴ — 1 = 15. Egli capì che se n non era primo allora non c'era modo che 2ⁿ — 1 lo fosse. Ma affermò con baldanza che, per valori di n , non superiori a 257, 2ⁿ — 1 sarebbe risultato primo solo e soltanto se n fosse stato uguale a uno dei seguenti numeri: 2, 3, 5, 7, 13, 19, 31, 67, 127, 257. Aveva scoperto un fatto seccante: persine quando n era un numero primo, ciò non garantiva che 2ⁿ — 1 lo fosse. Mersenne era in grado di calcolare a mano 2¹¹ — 1, ottenendo 2.047, che è uguale a 23 X 89. Generazioni di matematici si sono stupiti della capacità di Mersenne di asserire che un numero grande come 2²⁵⁷ — 1 fosse primo. È un numero dì 77 cifre. Possibile che il monaco avesse accesso a una qualche mistica formula aritmetica che gli diceva perché quel numero, assolutamente al di fuori delle capacità di calcolo umane, era primo?

I matematici ritengono che se si proseguisse nell'elenco di Mersenne, si troverebbero infiniti valori di n tali per cui i corrispondenti numeri di Mersenne 2ⁿ — 1 risultano numeri primi. Ma manca ancora una dimostrazione del fatto che questa supposizione sia vera. Siamo ancora in attesa di un Euclide dei nostri giorni che dimostri che i primi di Mersenne non si esauriscono mai.

Il Teorema dei numeri primi

Eulero, uno dei massimi matematici del Settecento, cercò di provare una delle più eleganti osservazioni di Fermat, un teorema concernente i numeri primi. Tutti i numeri primi possono essere suddivisi in due gruppi: quelli che equivalgono a 4n + 1 e quelli che equivalgono a 4n — 1, dove n sta per un qualche numero. Ad esempio 13 appartiene al primo gruppo (4x3 + 1), mentre 19 appartiene al secondo gruppo (4 x 5 - 1). Il teorema di Fermat affermava che il primo tipo di numeri primi era sempre la somma di due quadrati (13 = 2² + 3²), mentre il secondo tipo non poteva mai essere espresso in questo modo (19 = ?² + ?²). Questa proprietà dei numeri primi è meravigliosamente semplice, ma cercare di dimostrarne la verità per ogni singolo numero primo si rivela notevolmente difficile. Per Fermat quella fu solo una tra le tante dimostrazioni che egli tenne per sé.

A Eulero si presentava la sfida di riscoprire la dimostrazione che aveva dato Fermat. Infine nel 1749, dopo sette anni di lavoro e a quasi un secolo dalla morte di Fermat, Eulero riuscì a dimostrare questo teorema sui numeri primi.

Si deve a Gauss l'importante passo di porsi una domanda diversa. Invece di cercare di prevedere la posizione precisa di un numero primo rispetto a quello precedente, egli tentò di capire se fosse possibile prevedere quanti fossero i numeri primi inferiori a 100, quanti quelli inferiori a 1.000 e cosi via. Dato un numero N qualsiasi, c'era un modo per stimare quanti fossero i primi compresi fra 1 e N? Per esempio, i numeri primi inferiori a 100 sono 25. Perciò, se scegliamo a caso un numero compreso fra 1 e 100, abbiamo una possibilità su quattro di pescare un numero primo. Come cambia questa proporzione quando si considerano i numeri compresi fra 1 e 1.000 o fra 1 e 10.000?

Armato delle sue tavole dei numeri primi, Gauss cominciò la ricerca. Osservando la frazione di numeri primi compresi in intervalli sempre più grandi, scoprì che cominciava a emergere una struttura. A dispetto della casualità di quei numeri, sembrava che nella nebbia si profilasse una stupefacente regolarità.

Se osserviamo la tabella di valori dei numeri primi compresi fra 1 e varie potenze di dieci riportata qui sotto, una tabella basata su metodi dì calcolo più moderni, questa regolarità diventa evidente.

La tabella, che contiene molte più informazioni di quelle di cui disponeva Gauss, ci mostra in modo chiaro la regolarità da lui scoperta. Ed è nell'ultima colonna che tale regolarità si manifesta. Questa colonna riporta la frazione di numeri primi rispetto a tutti i numeri considerati. Per esempio, quando si conta fino a 100, un numero su quattro è primo, così che in quest'intervallo dovremo aggiungere in media 4 per passare da un numero primo al successivo. Dei numeri minori di 10 milioni, 1 su 15 è primo.

Ciò che Gauss scopri è che per contare i numeri primi sipossono usare i logaritmi in base e, un numero speciale uguale, fino alla dodicesima cifra decimale, a 2,718 281 828 459... (come , questo numero ha un'espansione decimale infinita e sempre diversa). In matematica e si rivela importante quanto , e fa la sua comparsa in ogni angolo del mondo matematico. È per questo che i logaritmi in base e sono chiamati logaritmi «naturali».

La tabella che Gauss aveva costruito all'età di quindici anni lo portò a formulare l'ipotesi seguente. Per i numeri compresi fra 1 e N, ogni log(N) numeri ce ne sarà grossomodo 1 che è primo (dove log(N) rappresenta il logaritmo di N in base e). Perciò egli poteva stimare che i numeri primi compresi fra 1 e N fossero all'incirca N/log(N). Gauss non affermava che questo gli desse come per magia una formula esatta per calcolare quanti numeri primi fossero compresi fra 1 e N; solo che sembrava fornire un'ottima stima approssimata.

Se invece di chiedersi quali numeri fossero primi, si faceva un passo in dietro e ci si poneva la questione più ampia di quanti fossero i numeri primi inferiori a un milione, sembrava che emergesse una forte regolarità.

Seguendo l'esempio di Gauss, è diventata consuetudine denotare il numero di numeri primi compresi fra 1 e N con il simbolo (N) (che non ha nulla a che vedere con il numero . Gauss ebbe la sfortuna di adottare un simbolo che fa pensare alle circonferenze e al numero 3,1415... Pensatelo invece come un nuovo tasto della vostra calcolatrice. Inserite un numero N e premete il tasto (N), e la calcolatrice vi fornisce il numero di primi minori o uguali a N. Per esempio, (100) = 25 è il numero di primi non maggiori di 100, e (1.000) = 168.

Su questo piccolo ordine di grandezza il risultato è una scalinata nervosa, in cui è difficile prevedere quanto si debba aspettare prima di incontrare il gradino successivo. In queste dimensioni riusciamo a vedere ancora i dettagli minuti dei numeri primi.

I singoli gradini diventano insignificanti e ci troviamo a osservare l'andamento complessivo di questa funzione: un pendio che sale lentamente e con regolarità. Era questo il grande tema che Gauss aveva sentito ed era in grado di riprodurre usando la funzione logaritmo. Il fatto che il grafico salga in modo così regolare, a dispetto dell'estrema imprevedibilità dei numeri primi, è una delle più miracolose rivelazioni della matematica e rappresenta uno dei punti più alti nella storia dei numeri primi.

Gauss perfezionò ulteriormente la sua stima del numero di primi. Capì che la probabilità di incontrare un numero primo all'aumentare di N diminuisce. Il modello di Gauss prevede che il numero di numeri primi minori o uguali a N sia

In realtà Gauss fece un passo ulteriore per creare una funzione che chiamò logaritmo integrale e che si indica con Li(N). La formulazione di questa nuova funzione era basata su una leggera variazione della precedente somma di probabilità e si rivelò incredibilmente precisa. Un numero N aveva una probabilità pari a 1 su log(N) di essere primo.

La funzione zeta

La chiave per studiare la distribuzione dei numeri primi servendosi di quest'area particolare della matematica consiste nel trovare una funzione che fornisca informazioni sui numeri primi. Ne esistono diverse. La prima fu scoperta dal famoso matematico svizzero Leonhard Eulero, che nel 1740 introdusse una funzione da lui stesso denominata con la lettera greca « zeta » .

La « funzione zeta » di Eulero associa a ogni numero reale s maggiore di 1 un nuovo numero reale.

Per calcolare la funzione zeta per un dato valore di s, occorre calcolare il valore di una somma infinita:

Ovviamente, non è possibile eseguire questa somma aggiungendo i suoi infiniti termini uno alla volta. Esistono tuttavia metodi matematici opportuni per trovare il suo risultato. Forse vi sorprenderà sapere che, se s è maggiore di 1, la somma ha un valore finito. (Ecco perché Eulero limitò l'uso della funzione solo ai casi in cui s è maggiore di 1.) Intuitivamente, se s è maggiore di 1, i singoli termini 1/1^s, 1/2^s, 1/3^s, ..., della somma diventano sempre più piccoli, e lo fanno così velocemente che, nonostante se ne debbano aggiungere infiniti, il valore della somma sarà comunque finito. Un caso interessante è quello in cui s = 2. Lo stesso Eulero calcolò che .

Che cosa ha a che fare la funzione zeta con i numeri primi? Eulero dimostrò che per ogni numero (reale) s maggiore di 1, è uguale al prodotto infinito

dove il prodotto viene eseguito fra tutti i fattori nella forma

per tutti i numeri primi p.

Nonostante l'aria complicata della sua definizione come somma infinita, la funzione zeta ha alcune interessanti proprietà matematiche. In particolare, la sua rappresentazione grafica è una curva continua (senza interruzioni o impennate improvvise) e può pertanto essere studiata usando i metodi del calcolo infinitesimale.

Come funzione che parte da numeri reali e arriva a numeri reali, la funzione zeta è un oggetto monodimensionale, e pertanto, sebbene sia legata ai numeri primi dal prodotto infinito di Eulero, non ha una struttura geometrica sufficiente ad aiutarci a scoprire il modello della loro distribuzione. Per farlo, occorre muoversi in due dimensioni. Questo è proprio il passo fondamentale compiuto da Riemann. Egli sostituì il numero reale s con un numero complesso z, il che rese complessi anche i valori di .

Ora, esistono alcuni numeri complessi per i quali la somma infinita di Eulero non ha risultato. Una tecnica matematica sofisticata, tuttavia, nota come « continuazione analitica» può aiutarci.

L'ipotesi di Riemann

Con l'ipotesi di Riemann sì tentano dì comprendere gli oggetti più fondamentali della matematica: i numeri primi.

Poiché i numeri naturali sono punti appartenenti al piano complesso, tutti giacenti nella metà positiva dell'asse x, quando studiamo le proprietà di quest'ultimo possiamo a volte dedurre qualcosa a proposito dei numeri naturali. Lo studio dei numeri naturali che si avvale del calcolo infinitesimale (e di altre tecniche) per analizzare le proprietà di certe funzioni complesse è un'area fondamentale della matematica denominata « teoria analitica dei numeri». Il problema di Riemann appartiene alla teoria analitica dei numeri.

In casi come la funzione zeta, esiste un mezzo alternativo per calcolare i valori, che funziona con quasi tutti i numeri complessi, compresi tutti quelli per i quali la formula originale non da una risposta (o, se non tutti, comunque molti di essi). Per la stessa funzione zeta, il metodo alternativo ci consente di calcolare per ogni numero complesso z, con la sola eccezione del numero z = 1. Il processo mediante il quale si passa dalla definizione originale della funzione a quella alternativa è denominato «continuazione analitica». Poiché Riemann fu il primo a compiere questo passaggio, la funzione complessa è solitamente indicata come « funzione zeta di Riemann». Nel suo importantissimo articolo del 1859, Riemann usò la funzione zeta per indagare il modello di distribuzione dei numeri primi.

Il suo obiettivo originale era quello di dimostrare la congettura di Gauss, e cioè che, per grandi numeri n, la densità dei numeri primi minori di n, D(n) è approssimata da 1/ln(w): il risultato oggi noto come «teorema dei numeri primi ». Sebbene Riemann non avesse raggiunto quell'obiettivo, il suo lavoro effettivamente fornì un solido legame fra i numeri primi e la geometria del piano complesso. Inoltre, i suoi metodi fornirono la base per la dimostrazione del teorema dei numeri primi trovata infine da Hadamard e de la Vallèe Poussin nel 1896. Il legame fondamentale scoperto da Riemann fra la funzione zeta e i numeri primi era un'intima connessione tra la funzione di densità D(n) e le soluzioni dell'equazione = 0.

Qualsiasi numero complesso soddisfi questa equazione viene detto uno « zero » della funzione zeta. Nel suo articolo, lungo appena otto pagine, Riemann fece un'audace congettura sugli zeri della sua funzione zeta: cominciò osservando che ciascuno dei numeri —2, —4, —6,... è uno zero. In altre parole, = 0 ogni qualvolta z è un numero intero pari negativo. Poi passò a dimostrare che la funzione zeta, oltre a questi zeri reali, deve averne infiniti altri complessi. La sua congettura era che tutti quegli altri zeri avessero la forma z = 1/2 + bi, per un certo numero reale b. In altre parole, cominciavano tutti con 1/2. In termini geometrici, tutti gli zeri non reali della funzione zeta giacciono sulla linea retta appartenente al piano complesso che intercetta verticalmente l'asse x nel punto di ascissa 1/2 - la retta generalmente denominata «retta critica».

Hadamard e de la Vallèe Poussin non ebbero bisogno di questa congettura sugli zeri, oggi nota come ipotesi di Riemann, per dimostrare il teorema dei numeri primi. A quello scopo, infatti, si dimostrò sufficiente il nesso fra numeri primi e geometria del piano complesso fornito dalla funzione zeta di Riemann. L'ipotesi di Riemann, però, se vera, ha fondamentali implicazioni per la nostra conoscenza dei numeri primi. Riemann dimostrò che se tutti gli zeri complessi (non reali) della funzione zeta hanno una parte reale uguale a 1/2, allora la misura in cui la funzione di densità D(n) si discosta dalla curva 1/ln(w) varia in modo sistematicamente casuale, proprio come la proporzione di teste che si ottengono lanciando ripetutamente una moneta si discosta da 1/2. Ciò significa che, sebbene non sia possibile prevedere con una qualsiasi accuratezza la comparsa del prossimo numero primo, il modello complessivo dei numeri primi è estremamente regolare.

L'informazione aggiuntiva sul modello di distribuzione dei numeri primi che sarebbe fornita da una dimostrazione dell'ipotesi di Riemann avrebbe importanti ripercussioni non solo per la matematica. Sortirebbe anche fondamentali conseguenze per la sicurezza di quello che è ormai diventato un elemento essenziale della vita moderna: Internet.

Il paesaggio della funzione zeta

Riemann aveva scovato un passaggio che conduceva dal mondo familiare dei numeri a una matematica che sarebbe parsa assolutamente aliena ai matematici greci che avevano studiato i numeri primi duemila anni prima di lui. Egli aveva innocentemente mescolato i numeri immaginari con la sua funzione zeta, scoprendo, come un alchimista della matematica, il tesoro che emergeva da quella miscela di elementi, un tesoro che generazioni di matematici avevano cercato invano.

Riemann aveva stipato le sue idee in un saggio di dieci pagine, ma era del tutto consapevole del fatto che quelle idee avrebbero aperto vedute radicalmente nuove sui numeri primi.

Il punto da cui era partito Riemann per elaborare la sua teoria delle funzioni immaginarie era stato il lavoro compiuto da Cauchy, e per Cauchy una funzione era definita da un'equazione. Adesso Riemann aveva aggiunto l'idea che anche se l'equazione era il punto di partenza, era la geometria del grafico definito dall'equazione a essere davvero importante.

Il problema è che non è possibile disegnare il grafico completo di una funzione in cui sì inseriscono numeri immaginari. Per illustrare il suo grafico, Riemann aveva bisogno di lavorare in quattro dimensioni. Quale significato danno i matematici a una quarta dimensione? Chi ha letto i libri scritti da cosmologi come Stephen Hawking potrebbe legittimamente rispondere «il tempo». La verità è che noi matematici usiamo le dimensioni per seguire l'andamento di qualsiasi cosa ci possa interessare. In fisica ci sono tre dimensioni per lo spazio e una quarta dimensione per il tempo.

Per Riemann la funzione zeta era descritta da un analogo paesaggio in quattro dimensioni. Due dimensioni servivano a tracciare le coordinate dei numeri immaginari inseriti nella funzione zeta. La terza e la quarta dimensione si potevano poi utilizzare per registrare le due coordinate che descrivono il numero immaginario prodotto dalla funzione.

Il problema è che viviamo in uno spazio a tre dimensioni e perciò non possiamo basarci sul mondo visibile per comprendere questo nuovo «diagramma immaginario». Uno dei metodi migliori per comprenderli è guardare le ombre.

L'ombra che proiettiamo è un'immagine bidimensionale del nostro corpo tridimensionale. Se la si osserva da certe prospettive un'ombra fornisce poche informazioni, ma vista di profilo, per esempio, la silhouette di una persona può rivelare quanto basta per consentirci di riconoscerne il volto. In modo simile, possiamo costruire un'ombra tridimensionale del paesaggio a quattro dimensioni che Riemann creò usando la funzione zeta, un'ombra che conservi informazioni sufficienti a permetterci di cogliere le idee di Riemann.

La mappa bidimensionale dei numeri immaginari ideata da Gauss dà una rappresentazione grafica dei numeri che inseriremo nella funzione zeta. L'asse nord-sud registra il numero di passi che compiremo nella direzione immaginaria, mentre l'asse est-ovest rappresenta i numeri reali. Possiamo distendere questa mappa su un tavolo. Ciò che vogliamo fare è creare un paesaggio fisico situato nello spazio che sta al di sopra di questa mappa. L'ombra della funzione zeta si trasformerà allora in un oggetto fisico di cui potremo esplorare i picchi e le valli. L'altezza del paesaggio al di sopra di ciascun numero immaginario della mappa dovrebbe registrare il risultato che si ottiene inserendo quel numero nella funzione zeta. Per la stessa ragione per cui un'ombra mostra solo pochi dettagli di un oggetto tridimensionale, alcune informazioni vanno inevitabilmente perse nella costruzione grafica di un tale paesaggio. Ruotando l'oggetto, otteniamo ombre diverse che ne rivelano aspetti diversi. Analogamente, abbiamo a disposizione un certo numero di scelte riguardo a ciò che vogliamo che registri l'altezza del paesaggio al di sopra di ciascun numero immaginario della mappa stesa sul tavolo. Tuttavia è possibile scegliere un'ombra che racchiude informazioni sufficienti a permetterci di comprendere la scoperta di Riemann.

Ombra tridimensionale del paesaggio a quattro dimensioni della funzione zeta.

Quando Riemann cominciò a esplorare il paesaggio, s'imbattè in vari aspetti fondamentali della sua geografìa. Stando dentro il paesaggio zeta e guardando verso est, lo vedeva degradare verso una pianura uniforme che si elevava di un'unità sopra il livello del mare. Se si girava e procedeva verso ovest, vedeva una cresta di alture ondulate che correva da nord a sud. Le cime di queste alture erano tutte situate al dì sopra della linea che incrociava l'asse est-ovest in corrispondenza del numero 1. Sopra questo punto d'intersezione c'era un picco torreggiante che saliva in ciclo. Era, in effetti, infinitamente alto. Come aveva scoperto Eulero, quando si inserisce il numero 1 nella funzione zeta si ottiene un risultato che se ne va all'infinito. Dirigendosi a nord o a sud di questa vetta di altezza infinita, Riemann incontrava altri picchi. Nessuno di essi, tuttavia, era di altezza infinita. Il primo picco cadeva a un po' meno di 10 passi verso nord, in corrispondenza del numero immaginario 1 + (9,986...)i, e raggiungeva un'altezza di appena 1,4 unità circa.

Se Riemann avesse ruotato il paesaggio e riportato su un diagramma la sezione trasversale delle colline in corrispondenza di questa linea di divisione nord-sud passante per 1, avrebbe ottenuto qualcosa del genere:

Vista in sezione della catena di montagne che attraversa il paesaggio zeta da nord a sud. Questa sezione trasversale è stata tracciata lungo la linea crìtica nord-sud definita dal luogo dei punti con coordinata est pari a 1 unità.

Un aspetto cruciale del paesaggio non mancò di attrarre l'attenzione di Riemann. Sembrava che non ci fosse modo di usare la formula che definisce la funzione zeta per costruire il paesaggio a ovest, oltre la catena montuosa. Riemann aveva lo stesso problema che Eulero aveva incontrato inserendo numeri ordinari nella funzione zeta. Ogni volta che si inseriva un numero situato a ovest di 1, la formula che definisce la funzione zeta se ne andava inesorabilmente all'infinito. Eppure in questo paesaggio immaginario, a dispetto del picco che si innalzava all'infinito sopra il numero 1, le altre montagne della catena che correva da nord a sud sembravano percorribili.

Perché allora non procedevano nel loro andamento ondulato, a prescindere dai risultati prodotti dalla funzione zeta? Sicuramente il paesaggio non terminava lì, in corrispondenza di quella linea nord-sud. Possibile che non ci fosse nulla a ovest di quel confine? A dar fede soltanto alle equazioni, si sarebbe pensato che il paesaggio a est di 1 era tutto quello che si poteva costruire. Le equazioni non avevano alcun senso quando vi si inserivano numeri situati a ovest di 1.

Per fortuna Riemann non si lasciò disorientare dall'apparente intrattabilità della funzione zeta. La sua formazione lo aveva munito di una prospettiva che mancava ai matematici francesi. Egli riteneva che l'equazione su cui si fondava un paesaggio immaginario dovesse essere considerata come un aspetto secondario. Di importanza primaria era l'effettiva topografia quadridimensionale del paesaggio. Poteva ben darsi che le equazioni non avessero senso, ma la geometria del paesaggio suggeriva altrimenti. Riemann riuscì a trovare una formula con cui si poteva costruire il paesaggio mancante a ovest.

Quel nuovo paesaggio poteva poi essere saldato in modo perfetto al paesaggio originario. Ora un esploratore del mondo immaginario sarebbe potuto passare tranquillamente dalla regione definita dalla formula di Eulero al paesaggio creato dalla formula di Riemann senza nemmeno accorgersi di attraversare un confine.

A questo punto Riemann aveva a disposizione un paesaggio completo che ricopriva l'intera mappa dei numeri immaginari. Adesso era pronto a fare la mossa successiva. Durante gli studi di dottorato, aveva scoperto due fatti cruciali e impensabili su questi paesaggi immaginati. In primo luogo aveva appreso che possedevano una geometria straordinariamente rigida. C'era un solo modo per espanderli.

Ciò che poteva esistere a ovest era completamente determinato dalla geometria del paesaggio di Eulero a est. Riemann non poteva manipolare a proprio piacimento il suo nuovo paesaggio per creare alture ovunque gli andasse di farlo. Qualsiasi modifica avrebbe provocato uno strappo nella cucitura fra i due paesaggi. La totale rigidità di questi paesaggi immaginari era una scoperta importante. Riemann aveva scoperto che le alture e le valli presenti in una regione contengono informazioni sulla topografia dell'intero paesaggio.

Ma Riemann aveva fatto una seconda scoperta cruciale su quello strano nuovo tipo di matematica. Aveva scoperto quello che si potrebbe considerare il DNA dei paesaggi immaginari: ogni cartografo matematico che avesse saputo come tracciare sulla mappa immaginaria bidimensionale i punti in cui il paesaggio cadeva al livello del mare avrebbe potuto ricostruire la configurazione dell'intero paesaggio. La mappa che riportava questi punti era la mappa del tesoro di ogni paesaggio immaginario. Era una scoperta sbalorditiva. Un cartografo che vive nel nostro mondo reale non riuscirebbe a ricostruire le Alpi se gli si dicessero tutte le coordinate dei punti del mondo che si trovano al livello del mare. Ma in questi paesaggi immaginari la posizione di tutti i numeri immaginari in cui la funzione va a zero svela ogni cosa. Questi punti sono chiamati gli zeri della funzione zeta.

Gli astronomi sono avvezzi a dedurre la composizione chimica di pianeti lontani senza bisogno di visitarli. La luce proveniente da un pianeta può essere analizzata grazie alfa spettroscopia e contiene informazioni sufficienti a rivelarne la chimica. Questi zeri si comportano come lo spettro di luce emesso da un composto chimico. Riemann sapeva che la sola cosa che doveva fare era segnare tutti i punti della mappa in cui l'altezza del paesaggio zeta era uguale a zero. Le coordinate di tutti questi punti situati al livello del mare gli avrebbero dato informazioni sufficienti a ricostruire tutte le alture e gli avvallamenti al di sopra del livello del mare.

Riemann non aveva dimenticato quale era stato il punto di partenza della sua esplorazione. Il big bang che aveva creato quel paesaggio zeta era la formula con cui Eulero aveva definito la funzione zeta, una formula che, grazie al prodotto di Eulero, poteva essere costruita utilizzando solo i numeri primi. E se le due cose — i numeri primi e gli zeri della funzione zeta - producevano lo stesso paesaggio, Riemann sapeva che un qualche nesso doveva legarle. Un unico oggetto costruito in due modi diversi. Fu il genio di Riemann a svelare come quelle due entità fossero due lati della stessa equazione.

Il collegamento che Riemann riuscì a trovare fra i numeri primi e i punti situati a livello del mare nel paesaggio zeta non avrebbe potuto essere più diretto. Gauss aveva tentato di stimare quanti fossero i primi compresi fra 1 e un qualsiasi numero N. Ma Riemann, usando le coordinate di quegli zeri, fu in grado dì creare una formula che forniva il numero esatto dei primi non maggiori di N.

La formula escogitata da Riemann aveva due ingredienti chiave. Il primo era una nuova funzione R(N) che serviva a valutare il numero di primi non maggiori di N e che in sostanza forniva una stima migliore di quella di Gauss. La nuova funzione produceva ancora degli errori, ma i calcoli di Riemann rivelavano che questi errori erano notevolmente più pìccoli di quelli prodotti dalla formula di Gauss.

Per fare un esempio, il logaritmo integrale di Gauss prediceva l'esistenza di 754 numeri primi in più di quanti ce ne fossero realmente nell'intervallo compreso fra 1 e 100 milioni. La funzione perfezionata introdotta da Riemann ne prediceva soltanto 97 in più, con un errore che era grosso modo pari a un millesimo dell'un per cento.

La tabella seguente evidenzia quanto sia più precìsa la nuova funzione di Riemann nella stima del numero di primi non maggiori di N per valori di N che vanno da 1O² a 1O¹⁶.

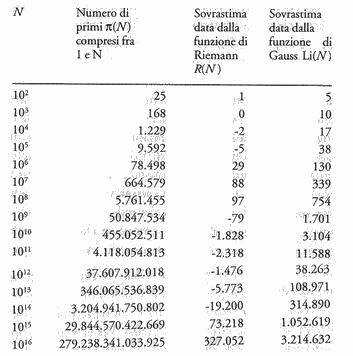
Ma se la nuova funzione di Riemann rappresentava un miglioramento rispetto alla funzione logaritmo di Gauss, produceva comunque degli errori. Tuttavia, l'escursione che Riemann aveva compiuto nel mondo immaginario gli diede accesso a qualcosa che Gauss non si sarebbe mai potuto sognare di ottenere: un metodo per eliminare quegli errori. Riemann comprese che utilizzando i punti della mappa dei numeri immaginati che segnavano Ì luoghi in cui il paesaggio zeta era al livello del mare, poteva disfarsi di quegli errori e ottenere una formula esatta per il conteggio dei numeri primi. Era questo ìl secondo ingrediente chiave della sua formula.

Eulero aveva fatto una scoperta sorprendente: se si inseriva un numero immaginario nella funzione esponenziale si otteneva un'onda sinusoidale. La curva in rapida ascesa che normalmente si associa alla funzione esponenziale veniva trasformata dall'introduzione di questi numeri complessi in una curva di andamento sìnuoso del tipo solitamente associato alle onde sonore. Questa scoperta diede avvio a una corsa all'esplorazione degli strani nessi portati alla luce dai numeri immaginari, Riemann comprese che era possibile estendere la scoperta di Eulero usando la sua mappa di punti corrispondenti agli zeri del paesaggio immaginario. In questo mondo oltre lo specchio riuscì a vedere come, usando la funzione zeta, ciascuno di quei punti poteva essere trasformato in una specìfica onda. Ogni onda avrebbe avuto l'aspetto di una variazione nel diagramma di una funzione seno.

Le caratteristiche di ciascuna onda erano determinate dalla posizione dello zero che ne era responsabile. Tanto più a nord si situava un punto a livello del mare, quanto più rapidamente l'onda corrispondente avrebbe oscillato. Se pensiamo a quest'onda come a un'onda sonora, la nota associata a uno zero risulta tanto più acuta quanto più a nord quello zero si situa nel paesaggio zeta.

Ma perché queste onde - queste note musicali — erano utili per il conteggio dei numeri primi? Riemann fece una scoperta stupefacente: nelle altezze variabili di quelle onde era codificato il modo per correggere gli errori presenti nella sua stima del numero di numeri primi. La funzione R(N) forniva una stima ragionevolmente buona del numero di primi minori o uguali a N. Ma aggiungendo a questa stima l'altezza di ciascuna onda al di sopra del numero N, egli scoprì che poteva ottenere il numero esatto di primi. L'errore era stato eliminato completamente. Riemann era riuscito a dissotterrare il Santo Graal che Gauss aveva cercato invano: una formula esatta per calcolare il numero di primi minori o uguali a N.

L'equazione che esprime questa scoperta può essere riassunta in parole semplicemente come «numeri primi = zeri = onde».

Per un matematico, la formula di Riemann che fornisce il numero di primi in termini di zeri ha un impatto pari a quello dell'equazione di Einstein E= mc², che rivelò l'esistenza di un legame diretto fra massa ed energia. Proprio come l'equazione di Einstein, questa è una formula di connessioni e trasformazioni. Riemann assistette passo passo alla metamorfosi dei numeri primi. I numeri primi creano il paesaggio zeta, e i punti che in quel paesaggio si trovano a livello del mare sono la chiave per scardinare i suoi segreti. Dopodiché emerge una nuova connessione in base alla quale ognuno di quei punti a livello del mare produce un'onda, una nota musicale. Infine Riemann ritornò al punto di partenza per mostrare come queste onde permettano di contare il numero esatto di numeri primi. Riemann deve essere rimasto strabiliato nel vedere il cerchio chiudersi in maniera tanto spettacolare.

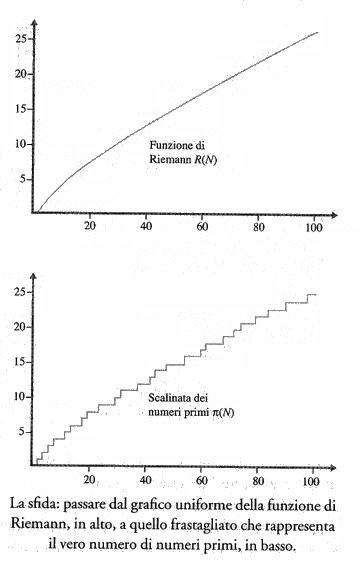
Riemann sapeva che, poiché esistono infiniti numeri primi, esistono infiniti punti che si trovano a livello del mare nel paesaggio zeta. Perciò devono esserci infinite onde che permettono di tenere sotto controllo gli errori. C'è un modo molto vivido per vedere come l'aggiunta di ogni onda supplementare migliori la stima del numero di numeri primi fornita dalla formula di Riemann. Prima dell'aggiunta delle onde corrispondenti agli zeri, il grafico della funzione di Riemann R(N) (riportato alla pagina seguente, in alto) non assomiglia affatto alla scalinata che rappresenta l'effettivo numero di numeri primi (in basso). Nel primo caso si ha una curva uniforme, nel secondo una curva frastagliata.

È sufficiente tener conto degli errori previsti dalle trenta onde create dai primi trenta zeri che incontriamo quando ci dirigiamo a nord nel paesaggio zeta per produrre un effetto evidentissimo. Il grafico di Riemann appare trasformato rispetto alla curva uniforme corrispondente a R(N) ed è molto più simile alla scalinata che descrive il numero effettivo di numeri primi:

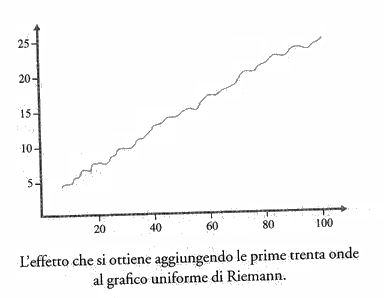
L'effetto che si ottiene aggiungendo le prime trenta onde al grafico uniforme di Riemann.

Ogni nuova onda rende un poco più contorta la curva perfettamente uniforme da cui si è partiti. Riemann comprese che qualora vi avesse aggiunto tutte le infinite onde, una per ogni punto a livello del mare che incontrava mentre proseguiva verso nord nel paesaggio zeta, la curva si sarebbe sovrapposta esattamente alla scalinata dei numeri primi.

Una generazione prima, Gauss aveva scoperto quella che riteneva fosse la moneta lanciata dalla Natura per scegliere i numeri primi. Le onde scoperte da Rìemann erano i risultati effettivi dei lanci fatti dalla Natura. Le altezze di ognuna dì quelle onde in corrispondenza del numero N predicevano per ogni lancio se la moneta dei numeri primi avrebbe dato testa o croce. Se la scoperta del legame fra numeri primi e logaritmi compiuta da Gauss aveva permesso di prevedere il comportamento medio dei numeri primi, Riemann aveva individuato ciò che controllava quel comportamento nei minimi dettagli.

(Tratto da "L'enigma dei numeri primi - Marcus Du Sautoy - BUR)

Link