NUMERI NATURALI. La matematica elementare riguarda essenzialmente certi elementi che si chiamano numeri, e certe operazioni che su di essi vengono definite. L'insieme infinito di simboli 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. . . che si usa per contare risponde al termine numeri naturali.
Per addizionare due di questi numeri, diciamo 5 e 7, partiamo da 5 (o da 7) e contiamo verso destra sette (o cinque) numeri ottenendo 12. La somma di due numeri naturali è ancora un numero naturale, cioè la somma di due elementi del suddetto insieme è ancora un elemento dello insieme. Per sottrarre 5 da 7 cominciamo da 7 e contiamo cinque numeri verso sinistra fino ad arrivare a 2. E' chiaro però che non si potrà sottrarre 7 da 5, dato che alla sinistra di 5 vi sono soltanto quattro numeri disponibili.
NUMERI INTERI. Per rendere sempre possibile la sottrazione è necessario ampliare il nostro insieme di numeri. Faremo precedere ogni numero naturale da un segno + (in pratica poi risulta più conveniente non scrivere questo segno) ed avremo i numeri interi positivi', facendo precedere un numero naturale dal segno — (e questo segno va sempre indicato) avremo un numero intero negativo', aggiungeremo poi un nuovo simbolo O, lo zero. Ora sull'insieme di numeri interi . . . ,-8,-7,-6,-5,-4,-3,-2,-1, O, +1, +2,+3, +4, +5, +6, +7, +8. ... le operazioni di addizione e sottrazione saranno possibili senza eccezioni.
Se m e n sono due numeri interi allora m + n, m — n, ed m x n sono interi, mentre m : n potrebbe non esserlo. Esiste inoltre un unico intero x tale che m + x = n. Se x = O, allora m = n ; se x è positivo (x > 0) risulta m minore di n (m < n), se x è negativo (x < 0) m risulta maggiore di n (m > n).
Ogni intero positivo m è divisibile per ±1 e per ±m. Un numero intero positivo m > 1 si definisce primo se i suoi unici fattori, o divisori, sono ± 1 e ±m; altrimenti m si chiama composto. Per esempio 2, 7, 19 sono numeri primi; 6 = 2x3, 18 = 2x3x3 e 30 = 2x3x5 sono numeri composti. Negli esempi precedenti i numeri composti sono stati espressi come prodotti dì fattori primi, fattori cioè che sono numeri primi.
NUMERI RAZIONALI. L'insieme dei numeri razionali è costituito da tutti i numeri della forma m/n, in cui m, n != O sono dei numeri interi; i numeri razionali comprendono perciò i numeri interi e le frazioni. Ogni numero razionale ha un'infinità di rappresentazioni; il numero intero 1 per esempio può essere rappresentato da 1/1, 2/2, 3/3, 4/4, ... la frazione 2/3 da 4/6, 6/9, 8/12, ... Una frazione si dice ridotta ai minimi termini m/n quando m ed n non hanno fattori primi comuni.
La regola più utile per i numeri razionali è quindi la seguente: il valore di un numero razionale non cambia se numeratore e denominatore vengono moltiplicati, o divisi, per lo stesso numero diverso da zero.
Quando si confrontano due numeri razionali è necessario porli nello stesso denominatore. Dei tanti denominatori (interi positivi) ce n'è sempre almeno uno che si chiama minimo comune denominatore. Per le frazioni 3/5 e 2/3 esso sarà 15; ne concludiamo che 3/5 < 2/3, essendo 3/5 = 9/15 < 10/15 = 2/3.
DECIMALI. Nello scrivere i numeri noi usiamo un sistema posizionale, cioè il valore attribuito ad una certa cifra dipende dalla sua posizione nella sequenza. Per esempio nel numero 423 il valore posizionale della cifra 4 è 4(100); nel numero 234 il valore posizionale della cifra 4 sarà invece 4(1). Dato che il valore posizionale di una cifra coinvolge il numero 10, questo sistema di nota-zioni si chiama sistema decimale. In questo sistema il numero 4238,75 significherà:
4(1000) + 2(100) + 3(10) + 8(1) + 7(1/10) + 5(1/100)
E' interessante notare che da questo esempio si possono ricavare certe definizioni da far valere più oltre nello studio degli esponenti. Essendo 1000 = 105, 100 = 1O2, 10 = 1O1 sembrerebbe naturale definire 1 = 100, 1/10= 1O-1, 1/100 - 1O2.
Col procedimento della divisione ogni numero razionale si può esprimere come un decimale; per esempio 70/33 = 2,121212. . . Questo è un numero decimale periodico: le cifre 12, dette ciclo, sì ripetono senza fine. Ogni decimale periodico rappresenta un numero razionale.
NUMERI IRRAZIONALI. L'esistenza di numeri diversi dai numeri razionali si può dedurre da una delle seguenti considerazioni:
(a) E' possibile immaginare un numero decimale non periodico infinito, ottenuto
disponendo a caso una successione di cifre.
(6) La lunghezza della diagonale dì un quadrato di lato 1 non è un numero razionale; non esiste cioè un numero razionale a per cui a2 = 2. Dei numeri come 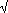 2, 3
2, 3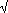 2, 5
2, 5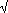 -3, e p si chiamano numeri irrazionali. I primi tre che abbiamo presentato si dicono radicali; il radicale sqrtn(a) è detto di ordine n. La lettera n è l'indice, a è il radicando.
-3, e p si chiamano numeri irrazionali. I primi tre che abbiamo presentato si dicono radicali; il radicale sqrtn(a) è detto di ordine n. La lettera n è l'indice, a è il radicando.
NUMERI REALI. L'insieme dei numeri reali è costituito dai numeri razionali e da quelli irrazionali.
NUMERI COMPLESSI. Nell'insieme dei numeri reali non esiste alcun numero il cui quadrato sia pari a —2. Se deve esserci un tale numero, cioè 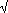 -2, allora per definizione (
-2, allora per definizione (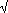 -22) = -2. Si faccia bene attenzione che dire (
-22) = -2. Si faccia bene attenzione che dire (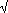 -22=
-22=
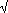 -2x
-2x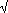 -2=
-2=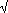 ((-2)(-2)) =
((-2)(-2)) = 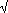 4 = 2 non è corretto; anche
4 = 2 non è corretto; anche 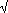 -2 x
-2 x 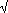 -3 =
-3 = 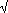 6 è scorretto. Per evitare questi errori si usa il simbolo i, dotato delle seguenti proprietà:
6 è scorretto. Per evitare questi errori si usa il simbolo i, dotato delle seguenti proprietà:
i numeri di forma a + bi, con a e b numeri reali, si dicono numeri complessi. Nel numero complesso a + bila. parte reale è a, la parte immaginaria è bi.
Il numero complesso a + bi coincide con un numero reale quando 6 = 0, con un numero immaginario puro quando a = 0. Quando il numero complesso non rientra nel novero dei numeri reali, lo si chiama immaginano.
Per sommare (o sottrarre) due numeri complessi, sommare (o sottrarre) le parti reali e poi sommare (o sottrarre) le parti immaginarie pure. Per moltipllcare due numeri complessi fare il prodotto come se i fosse un numero qualsiasi, sostituendo poi i2 con —1.
(Tratto da "Matematica Generale" di Frank Ayres Jr. - McGraw-Hill)


