Il 24 maggio 2000, a Parigi, in una sala del College de France, i due matematici di fama internazionale Sir Michael Atiyah e John Tate - il primo di nazionalità britannica, il secondo statunitense - annunciarono la messa in palio di un premio da un milione di dollari, da destinarsi alla persona (o alle persone) che per prima avesse risolto uno dei sette problemi matematici più difficili rimasti ancora insoluti. Tali problemi, essi dissero, sarebbero stati indicati, da quel momento in poi, come i «problemi del Millennio».

La somma di sette milioni di dollari - un milione per la soluzione di ciascun problema, senza limiti di tempo -era stata stanziata da Landon Clay, un ricco americano magnate dei fondi di investimento nonché appassionato di matematica. Un anno prima, Clay aveva fondato, nella sua città natale di Cambridge, nel Massachusetts, il Clay Mathematics Institute (CMI), un'organizzazione noprofit finalizzata alla promozione e al finanziamento della ricerca matematica. Il CMI, che aveva organizzato il meeting di Parigi, si sarebbe poi incaricato di gestire la competizione per i premi del Millennio.

I sette problemi erano stati selezionati nell'arco di diversi mesi da un piccolo gruppo di matematici di fama internazionale, scelti dalla commissione scientifica del CMI e guidati da Arthur Jaffe, direttore e fondatore del Clay Institute. Jaffe, già presidente dell'American Ma-thematical Society, è titolare della cattedra di matematica « Landon Clay » presso l'Università di Harvard. I membri della commissione ritenevano che i sette problemi prescelti fossero, fra quelli rimasti irrisolti, i più significativi della matematica contemporanea. La maggior parte dei matematici sarebbe d'accordo. I problemi del Millennio si collocano nel cuore stesso delle principali aree della matematica e hanno resistito ai tentativi di risoluzione compiuti da molti fra i migliori matematici del mondo.

Uno degli esperti che compilarono la lista è Sir Andrew Wiles, che sei anni prima aveva risolto l'ultimo teorema di Fermat: se questo enigma, antico di trecentotrenta anni, non è stato inserito nella lista del millennio, è grazie a lui. Gli altri esperti, oltre a Jaffe, erano Atiyah e Tate - che avevano parlato alla conferenza di Parigi - nonché Alain Connes e Edward Witten, di nazionalità rispettivamente francese e statunitense. Cosa alquanto strana, Landon Clay non è un matematico. A suo tempo, a Harvard, si specializzò in letteratura inglese. Successivamente ha istituito una cattedra di matematica presso la sua alma mater, quindi il Clay Mathematics Institute (il cui fondo di dotazione attualmente è di novanta milioni di dollari), e ora i premi del Millennio. In parte, stando a quanto lui stesso dichiara, queste iniziative furono una reazione alla penuria di finanziamenti pubblici destinati a una materia tanto importante. Offrendo un sostanzioso premio in denaro e invitando la stampa mondiale all'incontro in cui sarebbe stata indetta la competizione, Clay si assicurò che i problemi del Millennio - e, più in generale, la matematica - ottenessero l'attenzione dei media di tutto il mondo. Ma perché andare fino a Parigi per lanciare l'iniziativa?

La risposta è tutta nella storia. Esattamente cent'anni prima, nel 1900, Parigi aveva ospitato un evento simile in occasione del secondo Congresso internazionale della Matematica. L'8 agosto, il matematico tedesco David Hilbert, una figura di spicco a livello internazionale, fu chiamato a tenere un discorso durante il quale stabilì un programma di priorità per la matematica del ventesimo secolo. Nella sua conferenza, Hilbert elencò i ventitré problemi matematici irrisolti che riteneva più significativi. I «problemi di Hilbert», come divennero poi noti, rappresentarono veri e propri fari che guidarono i matematici verso il futuro.

Fra i problemi enunciati da Hilbert, alcuni si rivelarono molto più semplici di quanto egli avesse previsto, e ben presto furono risolti. Diversi altri erano formulati in modo troppo impreciso per ammettere una risposta definitiva. La maggior parte di essi, tuttavia, si dimostrò difficilissima. La soluzione di uno qualsiasi degli « autentici » problemi di Hilbert avrebbe reso il suo risolutore immediatamente famoso fra i matematici: una fama in tutto e per tutto simile a quella legata a un premio Nobel, con l'ulteriore vantaggio che il vittorioso matematico (tutti i risolutori furono di sesso maschile) non avrebbe dovuto attendere anni prima di godere i benefici del successo. Le gratificazioni arrivavano nel momento stesso in cui la comunità scientifica riconosceva la correttezza della soluzione proposta.

Con un'unica eccezione, nel 2000 tutti gli autentici problemi di Hilbert erano stati ormai risolti, e i tempi erano maturi perché i matematici tornassero a fare l'inventario: alla fine del secondo millennio, quali erano igrandi problemi irrisolti che tutti erano concordi nell'indicare come gli Everest della matematica?

In parte, l'incontro di Parigi fu un tentativo di ripetere la storia: non del tutto, però. Come ha sottolineato Wiles, lo scopo del CMI nel compilare l'elenco dei problemi del Millennio non era esattamente lo stesso che animò, a suo tempo, Hilbert. « Con i suoi problemi, Hilbert stava cercando di guidare la matematica », spiega Wiles. « Noi stiamo cercando di documentare fondamentali problemi irrisolti. In matematica esistono grandi problemi - problemi importanti - fra i quali però è diffìcilissimo isolarne uno che colga davvero l'essenza dell'impresa. » I problemi del Millennio, in altre parole, potrebbero non dare bene l'idea di dove sia diretta la matematica. Ciò nondimeno, essi ci offrono un'eccellente istantanea che mostra dove si trovino, oggi, le sue frontiere.

I sette problemi

Quali sono dunque i problemi del Millennio? Lo stato attuale della matematica è tale che nessuno di essi può essere descritto in modo appropriato senza poter contare su una considerevole preparazione.

L'ipotesi di Riemann.

Si tratta dell'ultimo problema rimasto irrisolto che faceva ancora parte della lista approntata da Hilbert nel 1900. I matematici di tutto il mondo sono concordi nel sostenere che questo interrogativo dal sapore arcano sulle possibili soluzioni di una particolare equazione sia il problema più significativo fra quelli ai quali la matematica è ancora in attesa di dare una risposta. Il problema fu formulato dal matematico tedesco Bernhard Riemann nel 1859, ed era emerso nel tentativo di rispondere a uno dei più antichi quesiti della matematica. La distribuzione dei numeri primi all'interno dei numeri naturali segue una legge? E in caso affermativo, quale? Nel III secolo a.C., il famoso matematico greco Euclide aveva dimostrato che i numeri primi continuano indefinitamente; in altre parole, che sono infiniti. Inoltre, a un esame empirico, i numeri primi sembrano « rarefarsi » e diventare sempre meno frequenti via via che si procede verso numeri più grandi. Ma è possibile affermare qualcosa di più in merito? La risposta, come vedremo nel capitolo 1, è « sì ». Una dimostrazione dell'ipotesi di Riemann migliorerebbe la nostra comprensione dei numeri primi e delle loro modalità di distribuzione. Né, d'altra parte, si limiterebbe a soddisfare la curiosità dei matematici: accanto a implicazioni matematiche che vanno ben oltre le regolarità riscontrabili nei numeri primi, la dimostrazione dell'ipotesi di Riemann avrebbe infatti ripercussioni sia sulla ìsica, sia sulla moderna tecnologia delle comunicazioni.

La teorìa di Yang-Mills e l'ipotesi del gap di massa.

I nuovi sviluppi della matematica traggono grande impulso dalla fisica. Nel diciassettesimo secolo, per esempio, furono proprio le esigenze della fisica a portare Isaac Newton e Gotfried Leibniz all'invenzione del calcolo infinitesimale, una tecnica che rivoluzionò la scienza dotando tutti i ricercatori di uno strumento matematico preciso per descrivere il moto continuo. Sebbene i metodi di Newton e Leibniz funzionassero, per elaborare la matematica alla base del calcolo infinitesimale occorsero tuttavia circa duecentocinquant'anni. Nel campo della fisica una situazione simile esiste anche oggi, relativamente ad alcune teorie che hanno visto la luce più o meno negli ultimi cinquant'anni. Per i matematici, il secondo problema del Millennio rappresenta un'ulteriore sfida a mettersi al passo con la fisica.

Le equazioni di Yang-Mills derivano dalla fisica quantistica e furono formulate circa cinquant'anni or sono dai fisici Chen-Ning Yang e Robert Mills per descrivere tutte le forze della natura, eccettuata la gravita. Funzionano benissimo: le previsioni ricavate da queste equazioni descrivono particelle che sono state poi osservate nei laboratori di tutto il mondo. Ma sebbene in termini pratici la teoria di Yang-Mills funzioni, essa attende ancora di essere elaborata come teoria matematica. Il secondo problema del Millennio richiede, in parte, proprio quello sviluppo matematico della teoria - sviluppo attualmente mancante - a partire dagli assiomi. La matematica dovrebbe soddisfare un certo numero di condizioni che sono state osservate in laboratorio. In particolare, dovrebbe confermare (dal punto di vista matematico) l'« ipotesi del gap di massa », riguardante le supposte soluzioni delle equazioni di Yang-Mills. Tale ipotesi è accettata dalla maggior parte dei fisici, e fornisce una spiegazione del perché gli elettroni siano dotati di massa. La dimostrazione dell'ipotesi del gap di massa è considerata un ottimo test per verifìcare lo sviluppo matematico della teoria di Yang-Mills. Allo stesso modo, essa si rivelerebbe preziosa anche per i fisici, giacché attualmente neanche loro sanno spiegare perché gli elettroni abbiano una massa, e si limitano a constatarlo.

Il problema P versus NP.

Questo è l'unico problema del Millennio che abbia a che fare con i computer e molti troveranno la cosa sorprendente. «Dopo tutto », diranno costoro, « oggi la matematica non si fa con i computer? » Be', no: in realtà non è così. Certo, la maggior parte dei calcoli numerici viene eseguita dai computer, ma il calcolo numerico è solo una parte piccolissima della matematica, e se è per questo non è nemmeno una parte rappresentativa. Sebbene i computer siano scaturiti dalla ricerca matematica - gli ultimi risultati matematici necessari alla loro creazione, avvenuta qualche anno dopo, furono elaborati negli anni Trenta - finora il mondo dell'informatica ha generato solo due problemi matematici che meriterebbero di essere inclusi fra i più importanti del mondo. Entrambi, più che'con strumenti o dispositivi di calcolo particolari, hanno a che fare col calcolo come processo concettuale, sebbene ciò non impedisca loro di avere importanti applicazioni ai fini del calcolo reale. Nella sua lista del 1900, Hilbert aveva incluso uno di tali problemi come numero 10. Quel problema - per sciogliere il quale si rende necessario dimostrare che certe equazioni non possono essere risolte da un computer -fu risolto nel 1970.

Il secondo problema è più recente. Si tratta di un interrogativo sull'efficienza con cui i computer possono risolvere problemi. Gli esperti di scienze informatiche suddividono i compiti computazionali in due categorie principali: compiti di tipo P, che possono essere affrontati efficacemente da un computer, e compiti di tipo E la cui soluzione potrebbe richiedere milioni di anni. Purtroppo, la maggior parte dei grandi problemi computazionali che sorgono nell'industria e nel commercio ricade in una terza categoria, NP, che sembra essere intermedia fra N ed E. Ma lo è davvero? Non potrebbe essere solo una versione mascherata di P? Moltissimi esperti credono che P e NP non siano la stessa cosa (in altre parole, che i compiti computazionali classificati rispettivamente di tipo NP e P non siano la stessa cosa). Dopo trent'anni di tentativi, però, finora nessuno è stato in grado di dimostrare se P e NP siano, o non siano, la medesima cosa. Una soluzione positiva avrebbe implicazioni significative per l'industria, il commercio e le comunicazioni elettroniche, compreso il World Wide Web.

Le equazioni di Navier-Stokes.

Le equazioni di Navier-Stokes descrivono il moto dei liquidi e dei gas — per esempio quello dell'acqua intorno allo scafo di un'imbarcazione, o quello dell'aria sulla superficie dell'ala di un aeroplano. Si tratta di quel genere di equazione che i matematici chiamano « equazioni alle derivate parziali». Gli studenti universitari di facoltà scientifiche e ingegneria imparano normalmente a risolverle, e le equazioni di Navier-Stokes sembrano esattamente simili a quelle assegnate loro come esercizio, reperibili nei manuali di calcolo infinitesimale. D'altra parte, le apparenze possono ingannare. Finora, nessuno ha idea di come trovare una formula che risolva queste particolari equazioni, e in effetti non sappiamo nemmeno se una formula del genere esista.

Ciò non ha impedito agli specialisti di ingegneria navale e aeronautica di progettare, rispettivamente, imbarcazioni efficienti e velivoli sempre migliori. Sebbene non esista una formula generale per risolvere queste equazioni (nel modo in cui, per esempio, la formula quadratica risolve tutte le equazioni di secondo grado), gli ingegneri impegnati nella progettazione di navi e aeroplani ad alte prestazioni possono comunque avvalersi dei computer per risolvere i singoli casi particolari di tali equazioni in modo approssimato. Come quello di Yang-Mills, il problema di Navier-Stokes è un altro caso in cui la matematica deve mettersi in pari rispetto a ciò che altri scienziati, nella fattispecie gli ingegneri, stanno già facendo.

Quel « mettersi in pari » potrebbe dare l'impressione che certi problemi siano importanti solo per l'orgoglio dei matematici, ai quali certo non piace esser lasciati indietro. Farsi quest'idea, d'altra parte, significherebbe fraintendere il modo in cui effettivamente avanzano le conoscenze scientifiche. In genere, la conoscenza matematica di un fenomeno rappresenta il modo più profondo e sicuro di penetrarlo, e questo a causa della natura astratta della matematica. Quanto più profondamente comprendiamo qualcosa, poi, tanto più riusciamo a trame vantaggio. Abbiamo già visto che una dimostrazione matematica dell'ipotesi del gap di massa costituirebbe un fondamentale progresso per la fisica; allo stesso modo, quasi sicuramente, anche la soluzione delle equazioni di Navier-Stokes condurrebbe a un progresso nel campo dell'ingegneria aeronautica.

La congettura di Poincaré.

Questo problema, sollevato dal matematico francese Henri Poincaré quasi un secolo fa, muove da un interrogativo apparentemente semplice: còme si fa a distinguere una mela da una ciambella? Sì, certo: questa davvero non sembra una domanda capace di generare un problema matematico da un milione di dollari. Quel che la rende difficile è che Poincaré desiderava una risposta matematica applicabile a situazioni più generali - il che ovviamente esclude il ricorso alle soluzioni più ovvie, per esempio quella di dare un morso a entrambe, mela e ciambella. Ecco come lo stesso Poincaré rispose a questa domanda. Se tendiamo un elastico intorno a una mela, possiamo poi farlo contrarre fino a ridurlo a un punto, muovendolo lentamente senza strapparlo e senza staccarlo dalla superficie. D'altra parte, se immaginate che lo stesso elastico sia stato teso in modo appropriato intorno a una ciambella, allora non c'è modo di ridurlo a un punto senza rompere l'elastico o la ciambella.

Sorprendentemente, nessuno è stato in grado di rispondere a chi si chieda se la stessa idea dell'elastico che si contrae possa servire a distinguere gli analoghi quadri-dimensionali di mele e ciambelle - ed era proprio questo che effettivamente interessava a Poincaré. La sua congettura afferma che l'idea dell'elastico effettivamente identifica mele quadri-dimensionali.

Questo problema è al cuore stesso della topologia, una delle branche più affascinanti della matematicacontemporanea. Oltre al suo fascino intrinseco e a volte bizzarro - per esempio ci insegna in che senso (un senso profondo e fondamentale) una ciambella e una tazza da caffè siano la stessa cosa - la topologia trova applicazioni in molte aree della matematica, e i suoi progressi hanno implicazioni nella progettazione e nella fabbricazione dei chip al silicio e di altre componenti elettroniche, come pure nei trasporti, nella comprensione del cervello e perfino nell'industria cinematografica.

La congettura di Birch e Swinnerton-Dyer.

Con questo problema, torniamo nella stessa area generale della matematica a cui fa capo l'ipotesi di Riemann. Fin dai tempi degli antichi Greci, i matematici hanno combattuto con il problema di descrivere tutte le soluzioni intere x, y, z a equazioni algebriche come

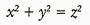
Per questa equazione particolare, Euclide trovò la soluzione completa; in altre parole, trovò una formula che genera tutte le soluzioni. Nel 1994, Andrew Wiles dimostrò che, per qualsiasi esponente n maggiore di 2, l'equazione

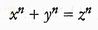
non ha soluzioni intere diverse da zero (questo risultato è noto come «ultimo teorema di Fermai»). Nel caso di equazioni più complicate, d'altra parte, diventa estremamente difficile scoprire se esistano delle soluzioni ed eventualmente individuare quali siano. La congettura di Birch e Swinnerton-Dyer ci fornisce informazioni sulle possibili soluzioni di alcuni di quei casi difficili.

Come nel caso dell'ipotesi di Riemann, a cui la congettura di Birch e Swinnerton-Dyer è collegata, una soluzione a questo problema contribuirebbe a migliorare la nostra comprensione dei numeri primi. Non è chiaro se possa avere implicazioni di portata paragonabile al di fuori della matematica. La dimostrazione della congettura di Birch e Swinnerton-Dyer potrebbe rivelarsi importante solo per i matematici.

D'altra parte, sarebbe stupido classificare questo o qualsiasi altro problema matematico come « privo di utilità pratica». Certo, i matematici che lavorano sui problemi astratti della « matematica pura » sono solitamente motivati più dalla curiosità che da qualsiasi conseguenza pratica. In moltissimi casi, d'altra parte, le scoperte nel campo della matematica pura hanno poi rivelato di avere importanti applicazioni pratiche.

Come se non bastasse, i metodi sviluppati dai matematici per risolvere un problema spesso si dimostrano applicabili ad altri problemi, completamente diversi. Questo fu sicuramente il caso della dimostrazione, data da Andrew Wiles, dell'ultimo teorema di Fermat. Allo stesso modo, quasi certamente, una dimostrazione della congettura di Birch e Swinnerton-Dyer comporterebbe l'emergere di nuove idee che in seguito potrebbero dimostrarsi utili ad altri scopi.

La congettura di Hodge.

Questo è un altro problema topologico che comporta un «pezzo mancante». In questo caso, l'interrogativo generale riguarda il modo in cui si possono costruire oggetti matematici complicati a partire da altri, più semplici. Di tutti i problemi del Millennio, per un profano questo è forse il più difficile da comprendere. Non tanto perché le intuizioni alla sua base siano in alcun modo più oscure di quelle degli altri problemi, o perché si ritenga che sia più difficile di uno qualsiasi di essi. Piuttosto, il fatto è che per sua natura la congettura di Hodge è altamente tecnica, giacché ha a che fare con le tecniche usate dai matematici per classificare certi tipi di oggetti astratti. Essa nasce da aspetti molto profondi della nostra disciplina, a un alto livellodi astrazione, e l'unico modo per afferrarla consiste nel procedere per livelli successivi di astrazione crescente. Ecco perché ho collocato questo problema per ultimo.

Il cammino intellettuale che portò alla congettura di Hodge iniziò nella prima metà del ventesimo secolo, quando i matematici scoprirono metodi potenti che consentivano di indagare la forma di oggetti complicati. L'idea fondamentale consisteva nel chiedersi in quale misura fosse possibile approssimare la forma d'un dato oggetto servendosi di unità geometriche semplici di dimensioni crescenti. Questa tecnica si rivelò così utile che venne generalizzata in molti modi diversi, portando infine allo sviluppo di strumenti potenti che permisero ai matematici di catalogare parecchi tipi di oggetti. Purtroppo, tale generalizzazione mascherò le origini geometriche della procedura, e i matematici dovettero aggiungere unità che non avevano alcuna interpretazione geometrica. La congettura di Hodge asserisce che, nel caso di un'importante classe di oggetti (denominati «varietà algebriche proiettive»), le unità denominate « cicli di Hodge » sono, ciò nondimeno, combinazioni di unità geometriche (denominate «cicli algebrici»).

Questi, sono dunque i problemi del Millennio; i più significativi problemi matematici ancora irrisolti al volgere del terzo millennio. Se leggendo la mia descrizione avete tratto una qualche conclusione su di essi, probabilmente si tratta della sensazione che siano tremendamente esoterici.

(Tratto da "I problemi del millennio - Keith Devlin- 2002 Longanesi & C.)