I tre problemi dell'antichità

La quadratura del cerchio consiste nel costruire un quadrato della stessa area di un cerchio dato; la duplicazione del cubo consiste nel costruire un cubo di volume doppio rispetto a quello dato; la trisezione dell'angolo consiste nel dividere un angolo in tre parti uguali. Dunque il primo problema riguarda le aree, il secondo i volumi, il terzo gli angoli.

Tutta questa storia si svolgeva nell'universo della geometria e che riguardava la costruzione delle figure. Chi dice costruzione dice strumenti: strumenti del pensiero, certo, ma anche strumenti materiali. Gli studiosi greci di geometria ammettevano soltanto per i loro metodi, l'uso della riga e del compasso.

Perché solo quei due strumenti e non altri? Perchè la riga è una linea retta; il compasso è il cerchio! Non si può trovare nulla di più elementare. Ecco che si spiega l'antica idea dei greci riportata negli 'Elementi' di Euclide. Per tracciarli, basta un solo gesto, per la retta, un lungo gesto della mano, per il cerchio, una rotazione regolare del pugno. Nell'universo della geometria greca, una figura esiste soltanto se è stata costruita mediante rette e cerchi.

La quadratura del cerchio

Già a Babilonia e in Egitto i matematici si erano interessati ai rapporti che univano il cerchio e il quadrato. Nel più antico testo matematico che sia stato rinvenuto, il papiro di Rhind, lo scriba Ahmes si prefiggeva di 'trovare un quadrato equivalente a un cerchio dato', proponendo di prendere in considerazione un quadrato col lato uguale a otto noni del diametro del cerchio. Questo naturalmente non era che un valore approssimativo, ma abbastanza accurato.

Più tardi, in Grecia, Anassagora di Clazomene, fu il primo greco a interessarsi alla questione. Anassagora si trovava in carcere, come prigioniero politico, quando si dedicò a risolvere il problema della quadratura. Ottenuto l'assenso degli altri prigionieri, prese a scrivere sulle pareti della cella, che ben presto furono tutte ricoperte di figure e di calcoli, ma senza risultato

Grazie all'intervento di Pericle, il fondatore della democrazia ateniese, che era stato suo allievo, Anassagora fu liberato; però, non sopportando di essere stato incarcerato ingiustamente, si suicidò. Il problema della quadratura gli sopravvisse.

Dopo lo scriba Ahmes, il problema aveva cambiato natura: non si trattava più di calcolare un valore approssimativo, ma di costruire un quadrato rigorosamente uguale a un cerchio. Poi venne Ippocrate di Chio.

Che Ippocrate fosse riuscito nella quadratura delle lunule aveva scitato uno scalpore enorme. Prima di lui, si era riusciti a ottenere la quadratura soltanto delle figure rettilinee, come rettangolo, parallelogramma, trapezio. Riuscendo a 'quadrare' una figura curva, Ippocrate alimentò speranze folli. Nessuno poteva più affermare che le superfici curve non si potessero 'quadrare'. Perché non il cerchio, allora?

Ippocrate stesso ci provò, ma fece un buco nell'acqua, come del resto tutti gli altri matematici greci dopo di lui.

La duplicazione del cubo

La prima volta che si sentì parlare di duplicazione del cubo, fu in occasione di una grande epidemia. La peste si era diffusa ad Atene e non si trovava nessun rimedio che riuscisse ad arrestarla. Una delegazione di ateniesi s'imbarcò per Delfi, allo scopo d'interrogare l'oracolo perché indicasse loro un modo per porre fine all'epidemia. L'oracolo si ritirò e la delegazione attese con impazienza il suo ritorno.

Ateniesi, per far cessare la peste, dovrete duplicare l'altare consacrato ad Apollo nell'isola di Delo.

L'altare di Apollo a Delo era celebre in tutta la Grecia per una quantità di ragioni, ma in particolare per la sua forma. Infatti era un cubo.

Gli ateniesi erano convinti che non ci fosse nulla di più semplice. Si recarono sull'isola e costruirono un nuovo altare, col lato doppio di quello antico.

La peste continuò, grande fu il loro disappunto, ma un saggio che passava di lì fece notare che il nuovo altare non era grande il doppio di quello antico, bensì otto volte più grande.

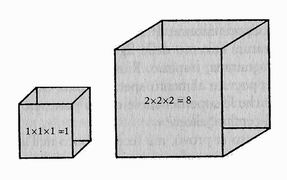
Gli ateniesi sbarcati sull'isola, decisero di distruggere il grande altare. Si misero al lavoro, ben decisi, stavolta, a dare soddisfazione all'oracolo. Sopra il vecchio altare, ne costruirono uno nuovo, identico sotto ogni aspetto a quello antico.

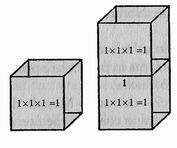
Il volume dei due altari riuniti era effettivamente il doppio di quello dell'altare originario. Soddisfatti, tornarono ad Atene congratulandosi, ma la peste continuò. Stavolta il furore e l'incomprensione regnavano sovrani. Non avevano forse costruito un altare che era doppio del precedente? Nient'affatto! Ciò che era doppio non era il volume di un unico altare, bensì di due.

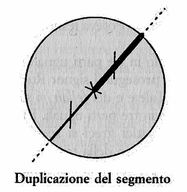
Gli ateniesi non capivano per quale motivo non riuscissero a risolvere un problema che sembrava così semplice. Duplicare un segmento? Non esiste nulla di più elementare.

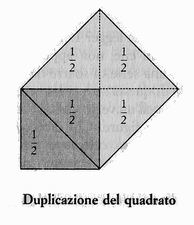
Duplicare un quadrato?. Gli ateniesi più colti sapevano che era possibile farlo costruendo sulla diagonale.

Allora perché, nonostante i loro sforzi, non riuscivano a duplicate il cubo?

Si accorsero di essere del tutto impotenti e così, disperati, decisero di fare appello ai più grandi matematici del tempo. Ce ne furono alcuni, che risolsero il problema a modo loro. Archita di Taranto ci riuscì realizzando l'intersezione di tre superfici: un cono, un cilindro e un prisma; Menecmo, invece, utilizzando due coniche, rispettivamente un'iperbole e una parabola. Ma il primo che osò trasgredire la legge della riga e del compasso fu Ippia di Elide, il sofista.

Ippia sapeva tutto di tutto, ed era quello che i greci definivano un polymathes: astronomia, musica, pittura, scultura, matematica. Era capace d'improvvisare un discorso su qualsiasi argomento e aveva una memoria prodigiosa che coltivava per mezzo di esercizi mnemotecnici. Da vecchio era ancora capace di recitare una lista di cinquanta nomi nello stesso ordine in cui li aveva sentiti. La sua abilità era celeberrima. Tutto ciò che indossava, lo aveva fabbricato da sé: tunica, calzari, cintura, fiala di profumo, cosmetici.

Da giovane era poverissimo, ma in vecchiaia aveva accumulato una fortuna immensa. La sua prosperità era cominciata quand'era arrivato in una città piccolissima nel cuore della Sicilia, Inycos, dove aveva guadagnato una somma di denaro enorme. Nessuno dice, però, in quale modo lo avesse guadagnato. Per lui, tutti i problemi erano problemi tecnici. Non si preoccupava troppo della teoria, non rinunciava a nessun espediente e ricorreva a tutte le astuzie possibili pur di raggiungere i suoi scopi.

E fu così che cominciò a guadagnare molto. La sua notevole abilità gli permetteva di trionfare in modo tecnico su tutti i problemi, persine la quadratura del cerchio, che riuscì a effettuare grazie alla 'quadratrice' che aveva messo a punto. Tre secoli dopo, Diocle, seguendo il suo esempio, inventò la 'cissoide', che gli permise di risolvere il problema della trisezione dell'angolo, e Nicomede, un secolo dopo, inventò una curva a forma di spirale, la 'concoide', che fece meraviglie tanto per la duplicazione del cubo quanto per la trisezione dell'angolo.

Tutte queste curve inventate dai matematici per risolvere i problemi erano curve meccaniche, non geometriche. In base alle leggi geometriche allora in vigore, si trattava di mezzi inferiori. Queste costruzioni avevano dunque un difetto di origine, dal momento che facevano intervenire il movimento e la velocità: punti che si muovono, rette che scivolano, figure che si spostano, tutti fenomeni proscritti dal mondo della geometria greca, che era un mondo statico. Queste costruzioni geniali, che però facevano intervenire elementi mobili, avevano un inconveniente grave, ai fini della costruzione del tempio di Delo: non erano realizzabili sul piano concreto.

Ora, l'oracolo l'aveva ordinato, quindi il tempio si doveva costruire davvero. Dunque gli inventori delle curve non avevano trovato la soluzione desiderata. La peste continuava, e così gli ateniesi si decisero a prendere in considerazione l'aspetto della filosofia e fecero visita a Piatone, all'Accademia. Ed ecco che cosa questi rispose loro: 'Se, per bocca dell'oracolo, Apollo ha imposto la costruzione di quell'altare, dovete capire che non è certo perché avesse bisogno di un altare doppio. Il punto è che rimproverava ai greci di trascurare la matematica e biasimava il loro disprezzo per la geometria.

Nel desiderio di risolvere a tutti i costi il problema non avete esitato a ricorrere a mezzi razionali e a utilizzare sistemi empirici. Così facendo, non perdete irrimediabilmente il meglio della geometria?.

E ad Atene la peste cessò.

La trisezione dell'angolo

Dividere un angolo in due parti uguali è possibile. La bisettrice è stata inventata per questo ed era facile da costruire.

Dividere un angolo in tre parti uguali non dovrebbe essere troppo complicato, tanto più che, grazie al teorema di Talete, si sapeva in quale modo dividere un segmento in tre parti uguali.

Errore! Anche su questo problema i matematici greci si scervellarono inutilmente.

(Tratto da "Il teorema del Pappagallo - Denis Guedj - 2003 TEA)