La prima cosa da dire a proposito di Pafnuty Lvovich Chebyshev è che il suo cognome è un incubo, Cebysev, Cebyshev, Chebichev, Chebycheff, Chebychev ecc. tutte trascrizioni differenti dello stesso nome.
E se quel nome insolito, Pafnuty, attira la vostra attenzione, non siete i soli. Attirò l'attenzione anche del matematico Philip J. Davis, verso il 1971. Davis si è imbarcato in una ricerca per trovare le origini di «Pafnuty», e ha scritto un libro davvero molto divertente in proposito, The Thread (Il filo, 1983). In breve il nome «Pafnuty», di origine copta (Papnute — «l'uomo di Dio»), venne introdotto in Europa dai cristiani egiziani ed era il nome di uno dei padri minori della Chiesa nel IV secolo. Al Concilio di Nicea, il vescovo Paphnutius (com'è trascritto di solito) argomentò contro il celibato ecclesiastico. Un Pafnuty successivo citato da Davis fu san Pafnuty di Borovsk, figlio di un nobile tartaro, che entrò in monastero a vent'anni e vi rimase fino alla morte, all'età di novantaquattro anni, nel 1478. Dice l'agiografo di questo Pafnuty: «Era puro e ascetico, e per questo grande taumaturgo e veggente».
Anche il nostro Pafnuty era in qualche modo capace di operare miracoli. Spetta a lui l'onore di aver ottenuto gli unici veri progressi verso una dimostrazione del TNP nel periodo che va dal rinvenimento della Chiave d'Oro a opera di Dirichlet nel 1837 all'uso che ne fece Riemann nel 1859. L'aspetto curioso è che il suo lavoro più originale non si incanalò nel flusso di ricerche sul TNP, ma diede inizio a un ramo minore del flusso, che rimase nascosto, per emergere soltanto cent'anni dopo.
Chebyshev dedicò in realtà due articoli al TNP. Il primo, del 1849, si intitola Sulla funzione che determina la totalità dei numeri primi minori di un dato limite (si noti la somiglianzà con il titolo del saggio scritto da Riemann dieci anni dopo). In questo lavoro Chebyshev raccoglieva la Chiave d'Oro di Eulero, ci giocherellava un poco come dodici anni prima aveva fatto Dirichlet e otteneva il seguente interessante primo risultato:
Se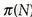 
è circa uguale a CN/log (N) per un certo numero fisso C,
allora C deve essere uguale a 1.
Il problema, naturalmente, era con quel «se». Chebyshev non fu in grado di superarlo e, per mezzo secolo, non potè farlo nessun altro.
Il secondo articolo di Chebyshev, del 1850, è molto più curioso. Invece di usare la Chiave d'Oro, partì con una formula dimostrata nel 1730 dal matematico scozzese James Stirling per ottenere i valori approssimativi della funzione fattoriale per numeri grandi. (Il fattoriale di N è 1x2x3x4x...xN. Il fattoriale di 5, per esempio, è 120: 1x2x3x4x5 = 120. Il simbolo convenzionale per indicare il fattoriale di N è «N!». La formula di Stirling dice che per grandi valori di N, il fattoriale di N è circa
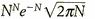
Chebyshev convertì questo risultato in una formula diversa che coinvolge una funzione gradino, ovvero una funzione che ha lo stesso valore per un certo intervallo, e poi salta a un altro valore.
Con questi pochi strumenti e alcuni passaggi di analisi elementare, Chebyshev ottenne due risultati importanti. Il primo era una dimostrazione del «postulato di Bertrand», proposto nel 1845 dal matematico francese Joseph Bertrand. Il postulato asserisce che tra un numero qualsiasi e il suo doppio (per esempio, tra 42 e 84) si può sempre trovare un numero primo. Il secondo risultato è il seguente:
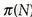non può differire da N / log (N) per più del dieci per cento circa in eccesso o in difetto.
Questo secondo articolo si rivelò importante per due aspetti. In primo luogo, l'introduzione di una funzione gradino potrebbe aver ispirato Riemann a usare una funzione simile nel suo saggio del 1859. Sicuramente Riemann conosceva il lavoro di Chebyshev: il nome del matematico russo compare negli appunti di Riemann (scritto come «Tschebyschev»).
È tuttavia il metodo adottato da Chebyshev in quel secondo lavoro che è maggiormente degno di nota. Egli ottenne i suoi risultati senza introdurre in alcun modo una teoria delle funzioni complesse. I matematici hanno un modo veloce per esprimere questo fatto. Dicono che i metodi di Chebyshev erano «elementari».
Riemann, nel suo articolo del 1859, non fece uso di metodi elementari. Applicò tutta la potenza della teoria delle funzioni complesse al suo oggetto di studio. I risultati conseguiti furono così straordinari che altri matematici seguirono la stessa strada, e il TNP fu finalmente dimostrato usando i metodi non elementari di Riemann.
Se fosse possibile dimostrare il TNP con metodi elementari rimase una questione aperta, ma dopo diversi decenni, era opinione comune che nessuna dimostrazione del genere fosse possibile. Così, nel suo testo del 1932 The Distribution of Prime Numbers (La distribuzione dei numeri primi), Albert Ingham afferma in una nota a piè di pagina: «[Una] dimostrazione "a variabile reale" del teorema dei numeri primi, ovvero una dimostrazione che non implichi in maniera esplicita o implicita il concetto di funzione analitica di una variabile complessa, non è mai stata trovata, e possiamo ora comprendere perché debba essere così...»
Invece, con gran stupore di tutti, una dimostrazione del genere è stata trovata nel 1949 da Atle Selberg, un matematico norvegese che lavorava all'Institute for Advanced Study di Princeton, nel New Jersey. Il risultato generò notevoli controversie, perché Selberg aveva comunicato alcune delle sue idee iniziali all'eccentrico matematico ungherese Paul Erdos, che se ne servì per produrre nello stesso tempo una propria dimostrazione. Due note biografie di Erdos vennero pubblicate dopo la sua morte nel 1996, e in entrambe il lettore curioso può trovare una descrizione esauriente della polemica. La dimostrazione è denominata in Ungheria dimostrazione di Erdós-Selberg, e dimostrazione di Selberg altrove.
Oltre a essere uno studioso, Chebyshev fu anche un ottimo insegnante capace di fare proseliti per la sua materia. I suoi studenti trasferirono le sue idee e i suoi metodi in altre università russe, stimolando l'interesse e migliorando il livello delle ricerche ovunque. Attivo fin oltre i settantanni, Chebyshev fu anche un acuto inventore, e costruì una serie di calcolatrici ancora conservate nei musei di Mosca e Parigi. Un cratere lunare porta il suo nome: si trova a circa 135° ovest 30° sud.
Non posso lasciare Chebyshev senza almeno ricordare il suo famoso filtro (famoso almeno tra i teorici dei numeri, credo).
Se dividete un numero primo (diverso da 2) per 4, il resto deve essere 1 o 3. Hanno qualche preferenza i numeri primi? Sì, ce l'hanno: fino a p = 101, ci sono 12 resti uguali a 1 e 13 resti uguali a 3. Fino a p = 1009, il conto da 81 e 87. Fino a p= 10007, si ha 609 e 620. Com'è ovvio, i resti uguali a 3 hanno un margine leggermente superiore rispetto ai resti uguali a 1. Questo è un esempio di un filtro di Chebyshev, commentato per la prima volta dal matematico russo in uno scritto del 1853. Questo particolare filtro viene poi violato per p = 26861, quando il resto 1 guadagna momentaneamente la prima posizione. Ma si tratta di un'anomalia soltanto temporanea: la prima vera zona di violazione è in corrispondenza degli 11 numeri primi nell'intervallo tra p = 616 877 e p = 617011. I resti pari a 1 conquistano il primato per soltanto 1939 dei primi 5,8 milioni di numeri primi, che rappresentano il limite al quale mi sono fermato. Non lo conquistano una sola volta negli ultimi 4 988 472 di questi numeri primi.
Se il divisore è 3, il filtro ha un effetto ancora più drammatico. Qui, il resto (a partire da p = 3) può essere 1 o 2, e il filtro è a 2. Questo filtro non è violato fino a p = 608981813029. Ora sì che questo è un filtro! Questa violazione è stata individuata nel 1978, da Carter Bays e Richard Hudson.
(Tratto da "L'ossessione dei numeri primi - John Derbyshire - Bollati Boringhieri 2002)
Il Teorema dei Numeri Primi
