La « funzione zeta » di Eulero associa a ogni numero reale s maggiore di 1 un nuovo numero reale.

Per calcolare la funzione zeta per un dato valore di s, occorre calcolare il valore di una somma infinita:

La serie armonica

Si tratta di quello che i matematici chiamano serie, una somma di termini che continua all'infinito, i cui elementi seguono una qual che progressione logica. Qui i termini sono il reciproco dei numeri naturali ordinari 1, 2, 3, 4, 5, 6, 7 ...

La serie è abbastanza importante tanto che i matematici le hanno dato un nome, e l'hanno chiamata serie armonica.

La serie armonica ha somma infinita.

La dimostrazione fu proposta nel tardo Medioevo da uno studioso francese, Nicola di Oresme (1323 circa - 1382).

Oresme osservò che (1/3 + 1/4) è maggiore di 1/2, lo stesso vale per (1/5 + 1/6 + 1/7 + 1/8) e così via. In altre parole, se prendiamo prima 2 termini, poi 4, poi 8, poi 16, e così via, possiamo raggruppare la serie in un numero infinito di gruppi, ognuno dei quali è maggiore di 1/2. La somma totale deve perciò essere infinita.

Il problema di Basilea

Si trovi una forma chiusa per la serie infinita

Il problema di Basilea prende il nome dalla città svizzera sede dell'università in cui insegnarono successivamente matematica due dei fratelli Bernoulli (Jakob dal 1687 al 1705, e Johann dal 1705 al 1748).

Si noti che la serie studiata dal problema di Basilea (la chiamerò «serie di Basilea») non è molto diversa dalla serie armonica. Ogni termine è, infatti, il quadrato del termine corrispondente nella serie armonica. Ora, se calcolate il quadrato di un numero minore di 1, ottenete un numero ancora più piccolo; il quadrato di un mezzo è un quarto, che è più piccolo. Minore è il numero di partenza, più evidente è l'effetto: un quarto è solo di poco più piccolo di un mezzo, ma il quadrato di un decimo è un centesimo, che è molto più piccolo di un decimo.

Ogni termine nella serie di Basilea è quindi minore del termine corrispondente nella serie armonica e procedendo si ottengono termini molto più piccoli. Dal momento che la serie armonica diverge per poco, non è troppo sperare che la serie di Basilea, composta di termini sempre più piccoli, converga. Il calcolo suggerisce che è effettivamente così. La somma della serie a 10 termini è 1,5497677..., la somma a 100 termini è 1,6349839..., la somma a 1000 termini è 1,6439345..., e la somma a 10000 termini è 1,6448340... Sembra davvero che converga a un qualche numero prossimo a 1,644 o 1,645. Ma a quale numero?

In situazioni del genere, i matematici non si accontentano di ottenere solo un'approssimazione, soprattutto quando la serie in esame converge piuttosto lentamente, come in questo caso. (La somma a 10000 termini differisce solo per lo 0,006 per cento dalla somma vera, finale, infinita, che è 1,6449340668...) La risposta è forse una frazione, 9108/5537, o 560837 199/340948133? O qualcosa di più complicato, con magari una radice quadrata di 46/17, o la radice quinta di 11983/995, o la radice diciottesima di 7766? Che cosa e? Un profano potrebbe pensare che sia sufficiente conoscere il numero di una mezza dozzina di decimali. No: i matematici vogliono conoscere il numero esattamente, se possono. Non solo perché sono bizzarri fino all'ossessione, ma perché sanno per esperienza che ottenere quel valore esatto apre porte inaspettate, e getta luce sulla matematica sottostante. Il termine tecnico matematico per questa rappresentazione esatta di un numero è «forma chiusa». Una semplice approssimazione decimale, per quanto buona, è una «forma aperta». Il numero 1,6449340668... è una forma aperta. Osservate: quei tre puntini vi dicono che il numero è aperto all'estremità destra, perché voi possiate calcolare qualche cifra in più, se volete.

Quello era il problema di Basilea: trovare una forma chiusa per la serie dei quadrati reciproci. Il problema venne infine risolto nel 1735, quarantasei anni dopo il suo enunciato, dal giovane Eulero, che lavorava duramente a San Pìetroburgo.

La stupefacente risposta era

Si tratta del familiare , il numero magico 3,14159265..., il rapporto tra la circonferenza e il diametro del cerchio. Che cosa c'entra in un problema che non ha niente a che fare con i cerchi, o con la geometria in generale? Tutto questo non è molto sorprendente per i matematici moderni, che sono abituati a vedere da tutte le parti, ma nel 1735 suonava molto strano.

La soluzione di Eulero del problema di Basilea fornì non soltanto una forma chiusa per la serie del reciproco dei quadrati: come sottoprodotto, fornì anche forme chiuse per 1 + 1/2⁴ + + 1/3⁴+1/4⁴+1/5⁴ + ..., 1 + 1/2⁶+1/3⁶+1/4⁶+1/5⁶+..., e così via. A condizione che N sia un numero pari, il risultato di Eulero fornisce il valore preciso, come forma chiusa, della serie infinita indicata all'inizio del pragrafo

Quando N vale 2, la serie converge a ²/6

Quando N vale 4, la serie converge a ⁴/90

Quando N vale 6, la serie converge a ⁶/945

L'argomentazione di Eulero fornì una risposta per ogni numero pari N. Egli stesso, in una pubblicazione successiva, esplicitò i calcoli fino a N = 26, quando la serie converge a 1315 8627²⁶/11094481976030578125.

Che cosa accade però se N è un numero dispari? La soluzione di Eulero non ha nulla da dire in proposito. E nessun altro ha trovato un qualsiasi risultato nei successivi 260 anni e oltre. Non abbiamo idea di come possa essere la forma chiusa per 1 + 1/23 + 1/33 + + 1/43 + 1/53 + ... se mai ne esiste una, né l'equivalente per qualunque altro numero dispari. Nessuno è stato in grado di trovare una forma chiusa per queste serie. Sappiamo che convergono e possiamo naturalmente, con calcoli brutali, ottenere i valori con qualsiasi livello richiesto di accuratezza.

La funzione zeta di Riemann

Riemann elaborò la precedente funzione zeta di Eulero, sostituendo la lettera N con la lettera s

oppure scritta in maniera più coincisa:

Rivolgiamo la nostra attenzione a quell'argomento «s». Sappiamo che quando s vale 1 la serie diverge, e quindi la funzione zeta è indefinita.

Se invece s vale 2, 3, 4 ... la serie converge sempre, e abbiamo i valori per la funzione zeta. In effetti, possiamo mostrare che la serie converge per ogni numero maggiore di 1. Se s vale 1,5, la serie converge a 2,612375... Per s = 1,1, converge a 10,584448... Per s = 1,0001, converge a 10000,577222... Sembra strano che la serie diverga per s = 1, mentre converge per s = 1,0001. Questa è però una situazione comune in matematica. In effetti, quando s si approssima molto a 1, la funzione zeta si comporta in maniera molto simile a 1/(s — 1). Anche questa espressione è definita per qualunque numero s tranne che per s = 1, perché il denominatore in quel caso vale zero, e non possiamo dividere per zero.

Forse con un grafico le cose saranno più chiare. La figura 5.4 è un grafico della funzione zeta; Potete vedere che quando s si avvicina da destra al numero 1, il valore della funzione va all'infinito; e quando s va all'infinito all'estrema destra, il valore della funzione si avvicina sempre più a 1.

Il grafico non mostra alcuna parte della funzione a sinistra della curva s = 1. Questo perché finora ho assunto che s sia maggiore di 1.

Ma che cosa accade se non lo è? Ad esempio se s=0 allora tutti i termini elevati ad s valgono 1, quindi 1/1 è ancora 1 e la somma è 1 + 1 + 1 + 1 + 1 + 1 + 1 + ..., e ovviamente diverge. Se sommiamo 100 termini, il risultato è 100; se ne sommiamo 1000, il risultato è 1000; se ne sommiamo un milione, il risultato è un milione. Certo, diverge.

Per numeri negativi, le cose vanno anche peggio. Che valore ha l'espressione se s vale —1? 2^-1 è semplicemente 1/2, 3^-1 è semplicemente 1/3, e così via. Dal momento che l/(l/2) fa 2, l/(l/3) fa 3 ecc. la serie ha la forma 1 +2 + 3 + 4 + 5 + ... Senza dubbio divergente.

E che cosa accade se s = 1/2? Visto che 2^1/2 è proprio radice quadrata di 2 ecc., la serie diventa

Poiché la radice quadrata di un qualunque numero intero è più piccola del numero, ogni termine della serie è maggiore del corrispondente termine nella serie 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + + 1/7 +... Quella serie diverge, così anche questa deve divergere. Certo, se vi prendete la briga di calcolare davvero la somma e sommare i termini, vedrete che la somma dei primi dieci termini è 5,020997899..., dei primi cento termini è 18,589603824..., dei primi mille è 61,801008765..., dei primi diecimila è 198,544645449... e così via.

Il prodotto di Eulero

Usiamo adesso lo stesso concetto del Crivello di Eratostene applicandolo alla funzione zeta di Riemann

Moltipllcherò ora i due membri dell'equazione per 1/2^s, ottenendo

Sottrarrò ora la seconda di queste espressioni dalla prima

La sottrazione ha eliminato dalla somma infinita tutti i termini con numero pari, e sono rimasti solo quelli con denominatore dispari.

Ricordando il crivello di Eratostene, moltiplico ora ambo i membri dell'equazione per 1/3^s, dove 3 è il primo numero rimasto nel membro destro.

Sottraiamo ora questa espressione dalla precedente

Tutti i multipli di 3 sono scomparsi dalla somma infinita. Il primo numero rimasto a destra è ora 5

Notate l'analogia con il crivello di Eratostene? In realtà, dovreste in primo luogo notare la differenza. Nel crivello di Eratostene ho scelto di lasciare ogni numero primo originale, cancellando soltanto i suoi multipli di 2, 3, 4... In questo caso invece elimino il numero primo originale dal membro a destra nella sottrazione, insieme con tutti Ì suoi multipli.

Se continuo in questo modo fino a un numero primo sufficientemente grande, diciamo 997, ottengo questo

Ora, a destra, se s è un numero a piacere maggiore di 1, ho un numero solo di poco più grande di 1. Se s vale 3, per esempio, ho 1,00000006731036081534... Così non è molto lontano dal vero dire che se ripetessimo il processo per sempre, otterremmo il risultato indicato nella seguente espressione

per qualsiasi numero s maggiore di 1, in cui nel membro di sinistra si ha una espressione tra parentesi per ogni numero primo, che prosegue per sempre a sinistra. Se di volta in volta divido ogni membro ripetutamente per ciascuna delle espressioni tra parentesi, ottengo il risultato indicato nella seguente espressione

Posso scriverla in maniera più sintetica

C'è una maniera ancora più ordinata per scriverla. Ricordiamo il simbolo di sommatoria quando devo sommare un gran numero di termini della stessa forma, ebbene, esiste un simbolo equivalente per la moltiplicazione di termini della stessa forma, il simbolo prodotto, si tratta della lettera greca maiuscola «pi», che sta per «prodotto»

Sia la somma a sinistra che il prodotto a destra vanno in ogni caso all'infinito. Questo, in effetti, offre un'altra prova del fatto che i numeri primi non finiscono mai. Se finissero, la moltiplicazione a destra terminerebbe, portando dunque a un certo numero finito, per qualunque valore di s. Quando s=1, comunque, il membro sinistro si riduce alla serie armonica, che è una «somma infinita». Dal momento che non si può avere un infinito a sinistra uguale a un numero finito sulla destra, i numeri primi devono essere infiniti.

Il logaritmo Integrale

Consideriamo innanzitutto la funzione 1/log (t)

Ho ombreggiato un'area sottesa dal grafico, perché farò un'integrazione. L'integrazione, è un modo per calcolare l'area che sta sotto una funzione. Prima visualizzate l'integrale della funzione e poi mettete mano alla calcolatrice. Allora, qual è l'integrale di 1/log (t)?

Purtroppo, non esiste alcuna funzione ordinaria che si possa usare per esprimere l'integrale di 1/log (t). Questo integrale è comunque molto importante. Ricorre molto spesso nei nostri studi sull'ipotesi di Riemann.

Questa nuova funzione, introdotta da Gauss, prende il nome di «funzione logaritmo integrale». Il simbolo consueto per indicarla è Li(x). È definita come l'area sotto il grafico di 1/log (t), da zero a x.

Il calcolo implica un certo gioco di destrezza, perché 1/log (t) non è definita per t=1 (in quanto il logaritmo di 1 è zero). Nel calcolo degli integrali le aree al di sotto dell'asse orizzontale contano come negative, e quindi l'area alla destra di 1 va ad annullare l'area a sinistra, all'aumentare di t. In altre parole, Li(x) è l'area ombreggiata, dove l'area negativa a sinistra di t= 1 va a compensare l'area positiva a destra (quando x sta a destra).

La figura mostra un grafico di Li(x). Si noti che ha valori negativi quando x è minore di uno (perché quell'area è negativa), che va all'infinito negativo per x = 1 (come vi sareste aspettati), ma che al crescere di x a destra di 1 l'area positiva contribuisce sempre più ad annullare quella negativa, in modo che Li(x) ritorna dall'infinito negativo, raggiunge lo zero (e questo significa che l'area negativa è interamente annullata) a x= 1,4513692348828... e da quel punto in poi aumenta costantemente. Il suo gradiente è in ogni punto, naturalmente, 1/log (x). E vi prego di notare che quella è, la probabilità che un numero intero nelle vicinanze di x sia un numero primo.

Dunque è per questo motivo che tale funzione è così importante nella teoria dei numeri. Vedete, all'aumentare di N, Li(N) ~ N/log N. Ora, il TNP afferma che (N) ~ N/log N. Così se il TNP è vero, e noi sappiamo che lo è, dal momento che è stato dimostrato nel 1896, allora deve anche essere vero che (N) ~ Li(N).

Questo non è soltanto vero: è, per così dire, più vero. Intendo dire che Li(N) è in effetti una stima migliore di (N) rispetto a N/log N. Una stima molto migliore.

La tabella mostra che Li(x) è cruciale in tutto il nostro studio. In effetti, il TNP è spesso espresso come (N) ~ Li(N) piuttosto che come (N) ~ N/log N.

Versione evoluta del Teorema dei Numeri Primi

Per tutti i valori di N indicati, N/log N fornisce una stima inferiore rispetto a Li(N)

Rappresentazione grafica della funzione zeta

Se s > 1 la funzione zeta si esprime nella seguente maniera:

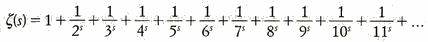
Una serie infinita, però, può definire soltanto parte di una funzione o, per metterla in termini matematici corretti, una serie infinita può definire una funzione solo su parte del suo dominio. Il resto della funzione potrebbe rimanere nascosto da qualche parte, in attesa di essere scoperto per mezzo di qualche trucco.

La funzione zeta è definita anche per valori minori di 1. In effetti ha un valore per ogni numero con l'unica eccezione di x — 1.

Si può rappresentare graficamente la funzione zeta in maniera frammentaria. Le seguenti figure mostrano i valori di 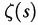per alcuni valori a sinistra di s=1.

Per i fattori di scala, «m» significa «milioni», «tr» significa «trilioni», «mtr» significa «milioni di trilioni», e «Mtr» significa «miliardi di trilioni».

In breve, quando s è appena minore di 1, il valore della funzione è molto grande ma negativo: come se, attraversando la linea s=1 verso ovest, il valore passasse improvvisamente da infinito a meno infinito. Se continuate a spostarvi verso ovest, ovvero avvicinando sempre più s a zero, la crescita rallenta in maniera drammatica. Quando s è zero, 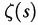è — 1/2. Per s = — 2, la curva attraversa l'asse s, e quindi 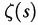vale zero. Dopo, la curva (stiamo ancora andando verso ovest) sale leggermente (in realtà fino a 0,009159890...) prima di girare verso il basso e attraversare di nuovo l'asse a s = — 4. Il grafico arriva in un modesto avvallamento (—0,003986441...) prima di aumentare di nuovo e attraversare l'asse a s = — 6. Un altro picco basso (0,004194), una diminuzione fino ad attraversare l'asse a s = - 8, un avvallamento un po' più profondo (— 0,007850880...), l'attraversamento dell'asse a —10, poi un picco davvero notevole (0,022730748...), l'attraversamento dell'asse a s = — 12, un profondo avvallamento ( — 0,093717308...), l'attraversamento dell'asse a s = — 14 e così via.

La funzione zeta vale zero per ogni numero pari negativo e ora i picchi e gli avvallamenti successivi diventano prsto sempre più e più pronunciati mentre si procede verso ovest. L'ultimo avvallamento che mostro, per s = -49,587622654..., ha una profondità di circa 305507128402512980000000. Potete comprendere la difficoltà di rappresentare graficamente la funzione zeta in un unico disegno.

Fin'ora abbiamo considerato s come variabile semplice (con la sola parte reale), in realtà s è una variabile complessa, cioè dotata di una parte reale e di una parte immaginaria e si muove sul piano complesso degli argomenti della funzione zeta.

La funzione zeta trasforma l'argomento s, nei valori complessi che stanno su un nuovo piano complesso chiamato il piano dei valori.

Nella figura sono contrassegnati tutti gli argomenti che danno un valore della funzione reale puro o immaginario puro. Verrà contrassegnato un argomento che dà valore 2 o —2, oppure 2i o —2i; un punto che da un valore 3 — 7i non sarà contrassegnato. Per dirlo in altre parole, saranno segnati tutti quei punti che zeta manda sulla retta reale o sulla retta immaginaria. E, del resto, poiché la retta reale e la retta immaginaria s'intersecano allo zero, gli argomenti in cui queste rette si intersecano, saranno zeri della funzione zeta. In questo modo, posso ottenere una rappresentazione della funzione zeta.

La funzione zeta manda il punto 1/2 + 14,134725z del piano degli argomenti nel punto 0 del piano dei valori.

La seguente figura mostra una gruppo di zeri intorno a 1/2+100i. Noterete che sono ammucchiati insieme più strettamente rispetto a quelli della figura precedente. In effetti la spaziatura media fra gli otto zeri indicati qui è 2,096673119... Per i cinque zeri mostrati nella figura precedente la distanza media era 4,7000841... Dunque qui intorno a 100; sull'asse immaginario, gli zeri hanno una densità più che doppia rispetto all'intorno di 20i.

Se estendo la figura precedente a sud lungo l'asse reale, le linee saranno speculari rispetto all'immagine a nord. L'unica differenza è che mentre i numeri reali che ho indicato nella figura precedente sono proprio gli stessi a sud come a nord, i numeri immaginari hanno segno invertito.

La conseguenza importante è che se a + bi è uno zero della funzione zeta, allora lo è anche a — bi.

Supponiamo adesso di volerci muovere verso nord a partire dall'argomento 1/2. Quale sarà il l'aspetto del valore della funzione zeta? La seguente figura ve lo mostra.

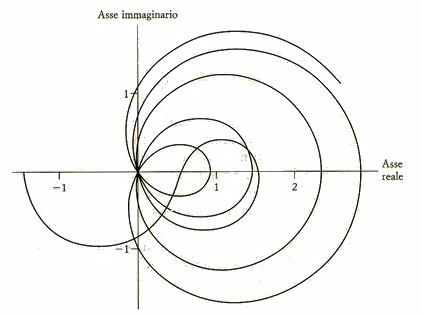
Il percorso inizia con s = 1/2 che vale -1,4603545088095... Poi compie una specie di semicerchio in senso antiorario sotto il punto zero, quindi gira e fa un anello in senso orario intorno a 1. Si dirige verso lo zero e lo oltrepassa (vale a dire il primo zero: l' argomento ha appena oltrepassato 1/2 + 14,134725i). Allora continua a percorrere cammini circolari in senso orario, attraversando il punto zero molto spesso, ogni volta che nel piano degli argomenti si passa su uno zero della funzione zeta.

L'ipotesi di Riemann

Tutti gli zeri non banali della funzione zeta hanno parte reale 1/2

Purtroppo tutti quei numeri pari negativi sono zeri banali. Dove sono quelli non banali? Sono sul piano complesso.

Nel 1900 erano note, con certezza matematica, le seguenti proprietà circa la posizione (la posizione sul piano complesso, voglio dire) degli zeri non banali.

- Ne esiste un'infinità, tutti con parte reale compresa tra O e 1 (esclusi). Servendosi del piano complesso per visualizzare il concetto i matematici affermano che è noto che tutti gli zeri non banali si trovano nella strìscia critica. L'ipotesi di Riemann fa un'affermazione molto più forte, ovvero che giacciono tutti sulla retta con parte reale pari a un mezzo, ovvero sulla retta critica. «Striscia critica» e «retta critica» sono espressioni tecniche comuni quando si discute dell'ipotesi di Riemann.

- Gli zeri si presentano in coppie coniugate. Ovvero, se a + bi è uno zero, allora lo è pure a — bi. In altre parole, se z è uno zero, lo è pure il suo complesso coniugato. In parole ancora diverse, se c'è uno zero sopra la retta reale, la sua immagine speculare al di sotto della retta reale è anche uno zero (e, naturalmente, viceversa).

Le prime informazioni concrete sugli zeri furono fornite dal matematico danese Jorgen Gram. Matematico dilettante senza alcun incarico universitario - era funzionario in una compagnia di assicurazioni - sembra che Gram avesse scarabocchiato per qualche anno metodi per calcolare davvero la posizione degli zeri non banali (questo accadeva ben prima dell'era del computer, naturalmente). Nel 1903, dopo aver messo a punto un metodo abbastanza efficace, pubblicò un elenco dei «primi» quindici zeri non banali, quelli prossimi e sopra alla retta reale. Gli zeri di Gram sono indicati nella seguente figura come punti lungo la retta critica. Il suo elenco, che conteneva alcune lievi imprecisioni nelle cifre all'estrema destra, comincia così:

1/2 + 14,134725i, 1/2 + 21,022040i,1/2 + 25,010856i...

Ognuno di questi numeri, come potete vedere, ha parte reale un mezzo. (E l'esistenza, naturalmente, implica un coniugato sotto l'asse reale: 1/2 — 14,134725i, e così via.) Dì conseguenza, più questi zeri si allontanano più confermano la verità dell'ipotesi di Riemann. Naturalmente però non vanno molto lontano. Sì sapeva che il numero di zeri era infinito, cosa implicita nel saggio di Riemann del 1859. Hanno tutti parte reale un mezzo? Riemann era di questa opinione. Quella era la sua ipotesi forte. A questo punto, tuttavia, nessuno ne aveva la minima idea.

Quando comparve l'elenco di Gram, i matematici dovettero contemplarlo con timore reverenziale. Il segreto della distribuzione dei numeri primi, che aveva catturato l'attenzione dei matematici fin dai giorni del leggendario Gauss, era incastonato in qualche maniera in questa sequenza di numeri: 1/2 + 14,134725i, 1/2 + 21,022040i, 1/2 + 25,010856i... Ma in quale maniera? Le parti reali di quei numeri erano certamente un mezzo, come Riemann aveva ipotizzato; ma le parti immaginarie non mostravano alcun ordine o schema regolare apparente.

Le ricerche in questa direzione sono continuate fino ai nostri giorni. Al congresso sull'ipotesi di Riemann tenutosi a Seattle del 1996, Andrew Odlyzko ha esposto la storia come riassunta nella seguente tabella

Van de Lune è riuscito a condurre le sue ricerche fino a trovare 5 miliardi di zeri alla fine del 2000 e 10 miliardi a ottobre del 2001. Nel frattempo, nel mese di agosto 2001, Sebastian Wedeniwski, usando il tempo di inattività di 550 personal computer dei laboratori di ricerca tedeschi della IBM, ha dato avvio a un progetto per proseguire oltre i calcoli. L'ultimo risultato comunicato da Wedeniwski porta la data del 1° agosto 2002, e segnala che il numero di zeri non banali con parte reale un mezzo è ora giunto a 100 miliardi.

(Tratto da "L'ossessione dei numeri primi - John Derbyshire - Bollati Boringhieri 2002)