Esercizi meccanica dei fluidi

		Fisica
Costanti Fisiche	Unità Misura	Esercizi Fisica	Applet Java	Test	Quesiti
Meccanica fluidi

Esercizio n. 1
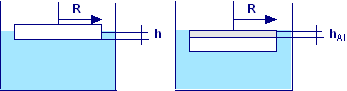
Un disco di plastica (densità ρ_p = 1150 kg/m³) di raggio R e spessore h_p = 2 cm galleggia in una vaschetta contenente un liquido di densità ρ_l = 1200 kg/m³. Si determini quale frazione del disco resta immersa nel liquido, in condizioni di equilibrio. Si determini poi qual è il minimo spessore h_Al che deve avere un disco di alluminio (densità ρ_Al = 2710 kg/m3) di raggio R che sovrapposto al disco di plastica faccia affondare l’insieme dei due dischi appena sotto il livello del liquido.
R.: 98,8 % ; 0,66 mm ;

Esercizio n. 2
Un pallone aereostatico (o mongolfiera) è, come noto, un pallone gonfiato di gas più leggero dell’aria e che perciò vola galleggiando nell’aria. Il tipo più semplice usa aria calda, ora ottenuta in genere con un bruciatore a gas liquido. Calcolare la temperatura minima T_min dell’aria necessaria per far salire un pallone di raggio R = 6 m e di massa totale M = 130 kg, se la temperatura dell’aria ambiente è T_amb = 20 °C (densità dell’aria a 20 °C ρaria 20°C = 1,2 kg/m³. Calcolare inoltre la quantità di gas liquido che si è dovuta usare per scaldare l’aria, sapendo che 1 kg di gas liquido, bruciando, fornisce 10000 kcal di calore. (Si consideri l’aria come un gas perfetto biatomico di peso molecolare m = 29 g/mol)
R.: 332 °K ; 0,92 kg ;

Esercizio n. 3
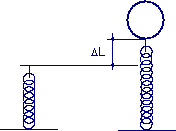
Una molla di costante elastica k = 90,0 N/m è ferma verticalmente su un tavolo. Un pallone di massa m_p = 2 g è riempito di elio (densità ρ_elio = 0,180 kg/m³) per un volume di 5,00 m³ ed è collegato alla molla causando il suo allungamento. Determinare la lunghezza dell’espansione ΔL della molla quando il pallone è in equilibrio. (densità ρ_aria = 1,29 kg/m³)
R.: 0,604 m ;

Esercizio n. 4
Un pallone di raggio 1 m pieno di elio (densità 0,2 kg/m³) è trattenuto mediante un filo con carico massimo di rottura di 50 N al pavimento di un ascensore. Calcolare il valore massimo dell’accelerazione con cui può scendere l’ascensore senza che la fune che regge il pallone si spezzi. Trascurare il peso della fune e dell’involucro del pallone. (densità dell’aria 1,29 kg/m³).
R.: 6,31 m/s² ;

Esercizio n. 5
Un bambino in una piscina spara orizzontalmente mediante una pistola giocattolo, ad una profondità di h₁ = 36 cm, una pallina con densità ρ. La pallina esce dall’acqua e raggiunge l’altezza massima di h₂ = 24 cm. Calcolare ρ, trascurando la resistenza dell’acqua e le forze di tensione superficiale.
R.: 0,6·10³ kg/m³ ;

Esercizio n. 6
Un recipiente, a pareti verticali, poggia su un piano orizzontale ed è riempito, fino all'altezza h = 25 cm, con una massa d'acqua m_a = 30 kg. In esso viene posto a galleggiare un cubo di ghiaccio di spigolo l = 20 cm. Si determini la pressione sul fondo, prima e dopo la fusione del ghiaccio (densità del ghiaccio ρ_gh = 940 kg/m³).
R.: (po+3067) N/m² ;

Esercizio n. 7
Un palloncino di gomma, che può sopportare una sovrappressione massima Δp = 0,66 atm, è riempito con elio alla pressione atmosferica. Nell'ipotesi di atmosfera isoterma secondo cui la densità dell'aria obbedisce alla legge di Boyle ρ = ρ_o·p/po, dove ρ_o e p_o sono la densità e la pressione al livello del mare, si calcoli a quale altezza dal suolo il palloncino esploderà. (ρ_o = 1, 29 kg/m³, p_o = 1 atm)
R.: 8,6 km ;

Esercizio n. 8
Una sfera omogenea, di volume V = 25 dm³ e densità ρ, è trattenuta, completamente immersa nell'acqua di un grande recipiente, da una funicella ideale ancorata al fondo, soggetta ad una tensione T = 20·g N. A causa della rottura della funicella, la sfera emerge raggiungendo una nuova posizione di equilibrio. Determinare la frazione di sfera emergente e la variazione della reazione vincolare esercitata dal fondo.
R.: 0,8 ; 196,2 N ;

Esercizio n. 9
Sul fondo di una piscina piena d'acqua è ancorata una fune ideale alla quale sono fissate, immerse nell'acqua e a distanze diverse, due boe A e B, entrambe di massa m = 3 kg e densità media ρ pari ad un terzo di quella dell'acqua. Determinare le tensioni T₁ e T₂ nei tratti di fune compresi tra il fondo e la prima boa A e tra la prima e la seconda boa B.
R.: 117,6 N ; 58,8 N ;

Esercizio n. 10
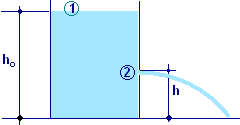
Un largo contenitore di raccolta è riempito fino ad un’altezza h_o. Il contenitore ha un buco ad altezza h dal fondo. Trovare un’espressione che descriva a quale distanza dal contenitore arriva il flusso d’acqua. Trovare il valore a cui deve essere praticato il foro per ottenere che la distanza a cui arriva il flusso d’acqua sia massima.


Esercizio n. 11
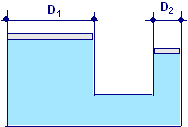
Se in un martinetto il pistone più grande ha raggio D₁ = 50 cm, qual è l’intensità della forza che è necessario applicare al pistone più piccolo di raggio D₂ = 5,0 cm, per sollevare un’automobile la cui massa è m = 1500 kg? Qual è il rapporto fra il lavoro fornito al dispositivo ed il lavoro prodotto?
R.: 147,15 N ; 1 ;

Esercizio n. 12
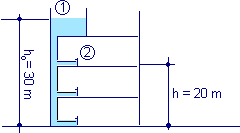
Il livello dell’acqua in un serbatoio sul tetto di un edificio è ad un’altezza da terra h_o = 30,0 m. Il serbatoio fornisce acqua attraverso condutture di sezione S₁ = 20,0 cm² ai vari appartamenti. Ogni rubinetto da cui esce acqua ha una sezione di apertura pari a S₂ = 10,0 cm². Calcolare: a) Il tempo necessario per riempire un secchio di 30,0 dm³ in un appartamento a 20,0 m sopra il livello della strada. b) La pressione differenziale nella condotta principale, a livello del suolo, a rubinetto chiuso ed a rubinetto aperto.
R.: 2,14 s ; 2,94·105 Pa ; 2,21·105 Pa ;

Esercizio n. 13
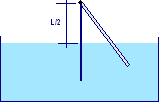
Un'asta di legno uniforme di lunghezza L e massa m = 0,3 kg è libera di ruotare attorno ad un asse orizzontale passante per un estremo, disposto ad un'altezza L/2 sopra la superficie libera dell'acqua contenuta in un grande recipiente. Sapendo che la densità del legno è ρ = 600 kg/m³, determinare la reazione vincolare sull'asse, quando l'asta è in posizione d'equilibrio.
R.: 0,5 N ; 1,13 N ;

Esercizio n. 14
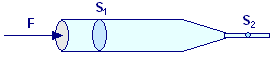
Una siringa ipodermica contiene una medicina con la densità dell’acqua. La canna della siringa ha una sezione di area S₁ = 2,50·10^–5 m² e l’ago ha una sezione di area S₂ = 1,00·10^–8 m². In assenza di una forza sul pistone, la pressione ovunque è di 1 atm. Una forza F di intensità 2,00 N agisce sul pistone, facendo si che la medicina schizzi orizzontalmente dall’ago. Determinare la velocità della medicina quando esce dalla punta dell’ago.
R.: 12,6 m/s ;

Esercizio n. 15
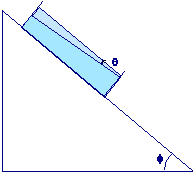
Un recipiente contenente un liquido scivola lungo un piano inclinato formante un angolo φ rispetto all'orizzontale. Il coefficiente di attrito cinetico tra recipiente e piano è μ = 0,15. Si determini l'angolo θ che la superficie libera del liquido forma col piano inclinato durante il moto del recipiente.
R.: 8,53° ;

Esercizio n. 16
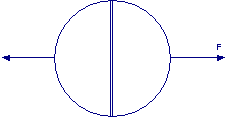
All’interno di due emisferi rigidi, a perfetta tenuta, la pressione viene ridotta a 1/4 di quella atmosferica. Se R è il raggio degli emisferi, determinare la forza F che occorre applicare a ognuno di essi per staccarli. Nell’ipotesi che R = 0.3 m e Δp = 0,1 atm, quale forza deve essere esercitata per separare i due emisferi?


Esercizio n. 17
Una boa cilindrica di massa m = 1450 Kg galleggia restando verticale in acqua salata (densità 1,03 g/cm³). Il diametro della boa è d = 0.9 m. a) Di quanto affonda la boa, quando un uomo di 68 Kg monta sulla sua sommità? b) Quanto vale il periodo di oscillazione del moto armonico semplice verticale, quando l’uomo si tuffa in acqua?
R.: 0,104 m ; 2,99 s ;

Esercizio n. 18
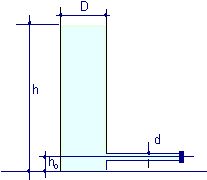
Un recipiente è costituito da un cilindro verticale, di diametro D = 9.0 cm , sul quale è innestato un tubo orizzontale, di diametro d = 3.0 cm, con asse ad una distanza h_o = 5.0 cm dal fondo del cilindro. All’altro estremo del tubo orizzontale viene posto un tappo e il recipiente viene riempito di acqua fino all’altezza h = 50 cm. Supponendo che il piano sul quale poggia il recipiente sia perfettamente liscio, determinare la forza F necessaria per mantenere fermo il recipiente quando viene tolto il tappo.
R.: 6,3 N ;

Esercizio n. 19
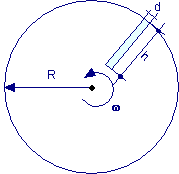
Un tubetto cilindrico, di lunghezza h = 20 cm e diametro d << h, pieno d’acqua e sigillato, viene fissato su di un disco orizzontale, di raggio R = 30 cm, in modo che il suo asse sia disposto lungo un raggio e una delle basi risulti allineata al bordo del disco. Determinare la differenza di pressione Δp tra le basi del tubetto quando il disco è in rotazione con una velocità angolare ω_o = 3600 giri/min.
R.: 5,7·106 Pa ;