Cinematica

Moto rettilineo uniforme

Dopo aver introdotto i concetti fondamentali che servono a studiare la cinematica, ossia traiettoria e legge oraria, velocità e accelerazione, andremo ora a studiare alcuni esempi particolari di moto. Il primo esempio di moto che consideriamo è il moto rettilineo uniforme, ossia un moto che avviene su una traiettoria rettilinea con velocità costante.

Nel moto rettilineo uniforme il sistema di riferimento è costituito da un solo asse cartesiano, che coincide con la traiettoria descritta dal corpo, e sul quale dobbiamo fissare un'origine, un'unità di misura per valutare le distanze e un verso positivo. Completate queste operazioni, ad ogni istante di tempo t il corpo occuperà un determinato punto lungo la traiettoria che verrà univocamente determinato dal valore dell'ascissa s sull'asse di riferimento. Dal momento che la velocità di un corpo v è definita come v = Δs / Δt, se v è costante anche il rapporto Δs / Δt è costante. Questo vuol dire che lo spazio percorso Δs e l'intervallo di tempo impiegato a percorrerlo Δt sono direttamente proporzionali.

Dalla definizione stessa di velocità possiamo ricavarci la legge oraria del moto rettilineo uniforme. Per prima cosa, invertendo la definizione di velocità, otteniamo: Δs = v · Δt, con v costante. Tale relazione può essere riscritta come s = s₀ + v · (t - t₀), dove s₀ è la posizione occupata dal corpo all'istante iniziale t₀, mentre s è la posizione occupata dal corpo all'istante di tempo generico t. Come caso particolare, consideriamo il caso in cui l'istante iniziale t₀ coincide con il momento in cui facciamo partire il cronometro. Allora possiamo porre t₀ = 0 e otteniamo: s - s₀ = v · t. Sommando s₀ ad entrambi i membri otteniamo finalmente la legge oraria del moto rettilineo uniforme: s = s₀ + v · t. Tale relazione ci dice che, per conoscere la posizione del corpo s ad ogni istante di tempo t, dobbiamo conoscere la posizione iniziale del corpo s₀ e la sua velocità v. Ad esempio se all'istante iniziale il corpo si trova a s₀ = 20 m dall'origine del sistema di riferimento e mantiene una velocità costante di v = 10 m / s, avremo che dopo un tempo t = 30 s il corpo si troverà a s = 20 m + 10 m / s · 30 s = 320 m dall'origine del sistema di riferimento.

Di seguito riportiamo il grafico spazio-tempo e il grafico velocità-tempo per il moto rettilineo uniforme: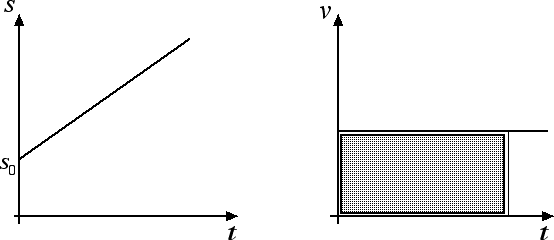

Per quanto riguardo il grafico spazio-tempo osserviamo come la pendenza della retta fornisca un'informazione relativa alla velocità del corpo in movimento: maggiore è la pendenza della retta, maggiore è la velocità del corpo.

Molto interessante è anche l'interpretazione geometrica del grafico velocità-tempo: l'area del rettangolo in figura infatti è uguale allo spazio percorso dal corpo in un intervallo di tempo uguale alla lunghezza della base del rettangolo. Ad esempio, se un corpo si muove a una velocità costante di v = 2 m / s, in un intervallo di tempo pari a 20 s percorrerà uno spazio pari a s = 2 m / s · 20 s = 40 m numericamente uguale all'area del rettangolo che ha per base l'intervallo di tempo e per altezza la velocità costante. Questa proprietà del grafico velocità-tempo rimane valida anche per moti diversi dal moto rettilineo uniforme: invece di ottenere una linea parallela all'asse delle ascisse avremo una curva generica ma l'area sottesa al grafico rimarrà numericamente uguale allo spazio percorso dal corpo.