Moto circolare uniforme

 

Moto nello spazio

Nelle ultime lezioni abbiamo sempre considerato moti che avvengono lungo una traiettoria rettilinea, ossia in un'unica dimensione. È importante tener presente che in generale i moti avvengono nello spazio e che la velocità e l'accelerazione sono entrambe caratterizzate da un'intensità, da una direzione e da un verso, in altre parole sono delle grandezze vettoriali.

Consideriamo ora una traiettoria curvilinea e cerchiamo di capire qual è la direzione del vettore velocità rispetto alla traiettoria. Ricordiamoci che la velocità è una variazione di posizione nell'unità di tempo, pertanto il vettore velocità avrà la stessa direzione della differenza di due vettori posizione, come nella seguente figura:

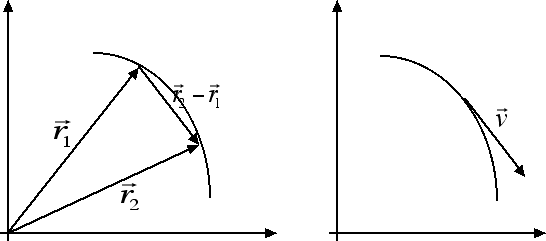
Quando l'intervallo di tempo diventa piccolo i due vettori posizione sono molto vicini e il vettore velocità istantanea diventa tangente alla curva, come emerge dalla figura di destra. Questa proprietà vale del tutto in generale: il vettore velocità istantanea è sempre tangente alla traiettoria descritta dal corpo. Non è invece possibile trovare una regola del tutto generale per stabilire la direzione del vettore accelerazione. Analizzeremo nelle prossime sezioni il caso particolare del moto circolare uniforme.

Prima di concludere questa sezione, vogliamo tornare al caso, già analizzato in passato, in cui un corpo è sottoposto a due vettori spostamento indipendenti che devono essere sommati con la regola del parallelogramma per ottenere lo spostamento totale. Chiaramente il vettore velocità (che è dato dal vettore spostamento diviso l'intervallo di tempo in cui tale spostamento avviene), eredita questa proprietà: ad esempio, anche per avere la velocità totale rispetto alla riva di un uomo che cammina su una barca è necessario sommare le singole velocità vettoriali (dell'uomo rispetto alla barca e della barca rispetto alla riva) con la solita regola del parallelogramma.