Condensatori

 

Differenza di potenziale

Supponiamo di avere due piastre metalliche parallele, poste a una piccola distanza e aventi cariche uguali ed opposte. Il campo elettrico che si crea tra le due piastre è uniforme e le linee di campo elettrico sono parallele tra loro, equidistanti e orientate dalla piastra carica positivamente a quella carica negativamente. In tal caso la forza elettrica F = q · E è la stessa in tutti i punti del campo. Di conseguenza, se vogliamo calcolare il lavoro necessario per spostare una carica elettrica da un punto all'altro del campo dobbiamo applicare la formula del lavoro di una forza costante: L = F · s = q E s, dove E è l'intensità del campo elettrico uniforme, q la carica che vogliamo spostare ed s il suo spostamento.

Ora, ricordiamoci che il lavoro che bisognava fare su una massa m per vincere il campo gravitazionale e portarla ad una certa altezza h rimaneva immagazzinato nella carica sotto forma di energia potenziale gravitazionale U = m · g · h. Qualcosa di analogo avviene nel caso del campo elettrico. Supponiamo di considerare sempre due piastre, una carica positivamente e l'altra carica negativamente, e il campo elettrico uniforme che si viene a creare.

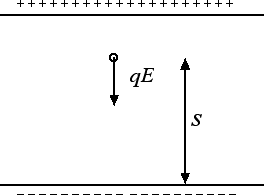
Per portare una carica positiva a una certa distanza dalla piastra negativa è necessario compiere un lavoro per vincere la forza elettrica L = q · E · s. Questo lavoro rimane immagazzinato sotto forma di energia potenziale elettrica. Se lasciamo la carica libera di muoversi, essa comincia a muoversi verso la piastra negativa convertendo progressivamente la sua energia potenziale elettrica in energia cinetica.

Se il campo elettrico è creato da una carica puntiforme il campo elettrico non è uniforme, ciò nonostante possiamo definire il concetto di lavoro L necessario per spostare una carica tra due punti del campo. Si può poi definire un'altra grandezza fisica che gioca un ruolo importantissimo in elettromagnetismo e che va sotto il nome di differenza di potenziale o tensione. La differenza di potenziale (d.d.p.) V_A - V_B fra due punti A e B si definisce come il rapporto tra il lavoro L_AB necessario per spostare la carica tra i due punti A e B e la carica stessa q. Dunque V_A - V_B = L_AB / q. L'unità di misura della d.d.p. nel Sistema Internazionale prende il nome di volt (simbolo V). Poiché nel Sistema Internazionale il lavoro si misura in joule (J) e la carica elettrica in coulomb (C) avremo: 1 V = 1 J / 1 C.

Nel caso particolare di un campo elettrico uniforme la differenza di potenziale tra il punto in cui si trova la carica q e la piastra carica negativamente è: V_A - V_B = L_AB / q = q E s / q = E s. La differenza di potenziale tra due punti dipende dall'intensità del campo elettrico E e dalla distanza s tra i due punti, ma non dipende dal valore q della carica di prova.

La differenza di potenziale consente di introdurre anche un'altra unità di misura per l'energia che viene spesso utilizzata dai fisici: l'elettronvolt (simbolo eV). Siccome dalla definizione di potenziale abbiamo che L_AB = q (V_A -V_B) definiremo 1 eV come l'energia necessaria per spostare la carica di un elettrone tra due punti fra i quali vi è una d.d.p. di 1 V. Siccome la carica di un elettrone vale q = - 1.6 · 10^-19 C avremo che 1 eV = 1.6 · 10^-19 J.