Equilibrio nei fluidi

Condizioni di galleggiamento

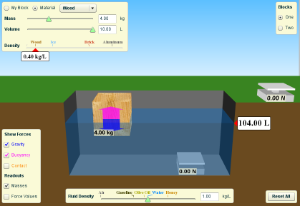
Nella sezione precedente abbiamo visto che un corpo immerso in un liquido è sottoposto a una forza diretta dal basso verso l'alto detta spinta di Archimede. Non dobbiamo però dimenticarci che sul corpo continua ad agire la forza-peso data da F_P = g · d_s · V, dove d_s è la densità del solido e V è il suo volume. La forza-peso F_P è diretta verticalmente dall'alto verso il basso e va confrontata con la spinta di Archimede S = g · d_l · V, diretta verticalmente dal basso verso l'alto. È chiaro che si possono presentare tre situazioni diverse a seconda dei valori che assumono la densità d_s del materiale di cui è costituito il solido immerso nel liquido e la densità d_l del liquido:

1. d_s > d_l: in questo caso la forza-peso è maggiore della spinta di Archimede e il corpo affonda.
2. d_s = d_l: in questo caso la forza-peso è uguale ed opposta alla spinta di Archimede. Il corpo rimane in equilibrio nel punto in cui lo abbiamo posto inizialmente.
3. d_s < d_l: in questo caso la spinta di Archimede ha la meglio sulla forza-peso perché la sua intensità è maggiore. Il corpo emerge e galleggia.

Nel terzo caso in cui il corpo galleggia siamo in grado di calcolare, partendo dalla spinta di Archimede, qual è il volume emerso e qual è il volume immerso nel liquido. Infatti quando il corpo galleggia abbiamo che la spinta di Archimede, uguale al peso del liquido spostato, è data da S = g · d_l · V_i, dove V_i è il volume del solido immerso nel liquido. Quando il corpo galleggia, la forza-peso F_P = g · d_s · V e la spinta di Archimede S = g · d_l · V_i si fanno equilibrio, ossia hanno la stessa intensità, da cui possiamo ricavare: d_s · V = d_l · V_i che implica V_i = V · d_s / d_l. Con questa formula possiamo calcolare qual è il volume del corpo che rimane immerso nell'acqua.

Quesito: Supponiamo di avere una pietra su una zattera posta in una piscina piena d'acqua. A un certo punto gettiamo la pietra nell'acqua. Il livello d'acqua nella piscina si alza o si abbassa?

Risposta: Per rispondere a questo quesito fissiamo per prima cosa dei dati: la densità della pietra è sicuramente maggiore della densità dell'acqua. Supponiamo ad esempio che il volume della pietra sia 20 l e la sua massa 60 kg. Quando la pietra è in equilibrio sulla zattera, la sua forza-peso pari a 60 kgp è esattamente compensata dalla spinta di Archimede, uguale al peso del liquido spostato. Dal momento che la densità dell'acqua è pari a 1 kg / l avremo che 60 kgp di liquido spostato equivalgono a un volume di 60 l d'acqua spostato. Quando invece la pietra è in fondo alla piscina sposta un volume d'acqua pari al suo volume, ossia 20 l. Pertanto la pietra sposta un volume d'acqua maggiore quando è sulla zattera, da cui possiamo concludere che gettando una pietra da una zattera il livello d'acqua nella piscina si abbassa.

Quesito: Considera un blocchetto di ghiaccio immerso in un bicchiere d'acqua. Determina se lo scioglimento del blocchetto di ghiaccio comporta un innalzamento del livello d'acqua nel bicchiere.

Risposta: Supponiamo, per fissare le idee, che il blocchetto di ghiaccio abbia una massa m = 0.1 kg. Prima di sciogliersi la forza peso del blocchetto, F_P = 0.1 kgp, è uguale ed opposta alla spinta di Archimede S = 0.1 kgp subita dal blocchetto stesso. Poiché la spinta di Archimede è uguale al peso del liquido spostato, abbiamo che l'inserimento del blocchetto di ghiaccio nel bicchiere sposta un volume d'acqua corrispondente a un peso di 0.1 kgp. Quando gli 0.1 kgp di ghiaccio fondono, per la conservazione della massa, si trasformano ancora in 0.1 kgp di acqua e dunque il livello d'acqua nel bicchiere rimane inalterato. Provare per credere!