|
|
|
|
|
Sollecitazioni in un arco parabolico a tre cerniere originate dal peso proprio strutturale. Esempio di calcolo.
Problema. Determinare le sollecitazioni nel punto D dell’arco parabolico a tre cerniere in figura.
Dati: L = 24 m, h = 4,8 m, xD = 10 m; sezione arco b= 20 cm, h = 50,1 cm, peso specifico legno
gl = 6,8 KN/m3.|
|
|
|
|
Il peso proprio g, riferito ad un metro di sviluppo dell’arco vale
![]()
|
|
L’equazione generale della parabola
riferita agli assi x ed y con origine in A diventa
La sua derivata prima, corrispondente alla tangente dell’angolo w rappresentato in figura, vale
|
Rispetto al riferimento cartesiano con origine in C ed assi x’,y’, l’equazione della parabola risulta
![]()
Calcolo delle reazioni vincolari
Per simmetria è
VA = VB
HA = HB
La reazione VA è pari al peso PAC dell’arco AC applicato nel suo baricentro.
Il peso PAC può essere ottenuto moltiplicando il peso proprio g, riferito ad un metro di sviluppo dell’arco, per la lunghezza lAC dello stesso arco PAC = g lAC.


![]()
(il valore della funzione per x = 0 è nullo)
![]()
VA = VB= 8,95 KN
Il momento statico dell’arco AC rispetto all’asse verticale passante per la cerniera C vale
![]()
![]()
![]()
La forza PAC è applicata ad una distanza dalla cerniera C pari a
![]()
![]()
Per il calcolo delle reazioni orizzontali è necessario il ricorso all’equazione ausiliaria, scritta per metà struttura. Imponendo l’azzeramento della sommatoria dei momenti nella cerniera C si ottiene
![]()
![]()
Calcolo delle sollecitazioni nella sezione D.
Nel sistema di riferimento con origine nella cerniera C, l’arco AD è caratterizzato dalle coordinate x’D = 12-10 = 2m e x’A = 12 m. La sua lunghezza risulta

Poiché il valore della funzione calcolata per L/2 è pari a lAC si ha
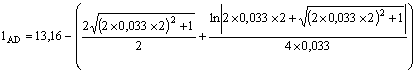
![]()
Il peso del tratto AD vale pertanto
![]()
Il momento statico dell’arco AC rispetto all’asse verticale passante per la cerniera C vale
![]()
![]()
![]()
La forza PAC è applicata ad una distanza dalla cerniera C pari a
![]()
![]()
Nel sistema di riferimento con origine nel punto A la sezione D ha coordinate xD = 10 m e
![]()
![]()
L’angolo w formato dalla tangente in D con l’orizzontale vale
![]()
![]()
|
|
|
![]()
![]()
| Argomenti correlati | |
| Lo studio geometrico di un arco parabolico | Sollecitazioni con due carichi uniformi |
| Proprietà delle funzioni iperboliche | Esempio di calcolo con due carichi uniformi |
| Caratteristiche geometriche di un arco parabolico | Sollecitazioni con peso proprio |
| Normativa per il calcolo del carico di neve su un arco parab. | Sollecitazioni con due carichi triangolari |
| Esempio di calcolo del carico di neve su un arco parabolico | Esempio di calcolo con due carichi triangolari |
| Sollecitazioni con un carico uniforme parziale | Sollecitazioni con due carichi triangolari parziali |
| Esempio di calcolo con un carico uniforme parziale | Esempio di calcolo con due carichi triangolari parziali |
| Scarica il foglio elettronico arcparab.zip (106 Kb) | |