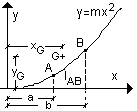
Caratteristiche geometriche di un arco parabolico
Problema. Determinare le espressioni analitiche della lunghezza lAB e delle coordinate xG e yG del baricentro G dell’arco parabolico AB in figura.
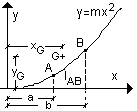
Il tratto elementare di parabola ha una lunghezza
dl pari a ![]()
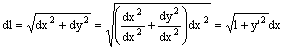
nella quale y’=2mx è la derivata prima della funzione parabolica
![]()
La lunghezza dell’arco AB è data da
![]()
I momenti statici dell’arco AB calcolati rispettivamente agli assi x ed y valgono
![]()
![]() .
.
Le coordinate del baricentro risultano quindi
![]()
![]()
Lunghezza dell’arco parabolico
![]()
![]()
![]()
Con il metodo di sostituzione si può porre 2mx = senh t, dove senh t è la funzione seno iperbolico della variabile di sostituzione t.
La trasformazione opposta è effettuabile tramite la funzione settorseno iperbolico
![]()
con
![]()
![]()
Essendo d(senh t) = cosh t dt e
![]() ,
,
si ha
![]()
![]()
Ricordando che
![]()
si ha
![]()
Si può ora applicare la regola di integrazione per somma ricordando che
![]()
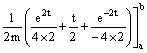

Essendo
![]()
si ha
![]()
![]()
Ripristinando la variabile originaria x si ottiene
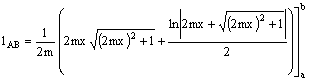
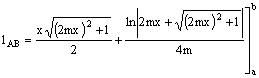
Momento statico rispetto all’asse y
![]()
![]()
![]()
![]()
Con il metodo di sostituzione si può porre 2mx = senh t, dove senh t è la funzione seno iperbolico della variabile di sostituzione t.
E’ quindi
![]()
![]()
Essendo d(senh t) = cosh t dt e
![]()
si ha
![]()
![]()
![]()
Poiché la derivata di
![]()
è
![]()
si ha
![]()
Essendo
![]()
![]()
![]()
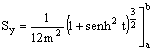
![]()
Ripristinando la variabile originale, si ottiene
![]()
L’arco uscente dall’origine ha momento statico
![]()
![]()
Momento statico rispetto all’asse x
![]()
![]()
![]()
![]()
Con il metodo di sostituzione si può porre 2mx = senh t, dove senh t è la funzione seno iperbolico della variabile di sostituzione t.
E’ quindi
![]()
![]()
Essendo d(senh t) = cosh t dt e
![]()
si ha
![]()
![]()
![]()
Essendo
![]()
si ha
![]()
Poiché è
![]()
si ha
![]() e
e
![]()
Si può ora applicare la regola di integrazione per somma ricordando che
![]()
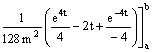
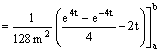
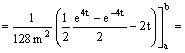
![]()
Poiché è
si ottiene
![]()
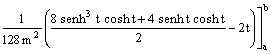
![]()
Ripristinando la variabile originale, si ottiene
![]()

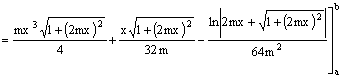
In definitiva si ottiene
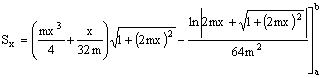
Esempio di calcolo
|
|
Si vogliono determinare la lunghezza e le coordinate baricentriche dell’arco parabolico OA della parabola
con xA = 2 m. |
m = 0,5
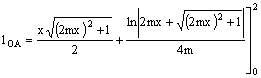
Risultando pari a zero il valore della funzione calcolata per x = 0, è sufficiente effettuare il calcolo per x = 2.

![]()
![]()
![]()
![]()
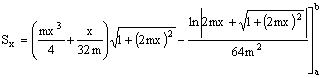
Risultando pari a zero il valore della funzione calcolata per x = 0, è sufficiente effettuare il calcolo per x = 2.
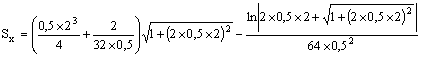
![]()
![]()
![]()
![]()
![]()
![]()
| Argomenti correlati | |
| Proprietà delle funzioni iperboliche | Sollecitazioni con due carichi uniformi |
| Caratteristiche geometriche di un arco parabolico | Esempio di calcolo con due carichi uniformi |
| Normativa per il calcolo del carico di neve su un arco parab. | Sollecitazioni con peso proprio |
| Esempio di calcolo del carico di neve su un arco parabolico | Esempio di calcolo con peso proprio |
| Sollecitazioni con un carico uniforme parziale | Sollecitazioni con due carichi triangolari |
| Esempio di calcolo con un carico uniforme parziale | Esempio di calcolo con due carichi triangolari |
| Scarica il foglio elettronico arcparab.zip (106 Kb) | Sollecitazioni con due carichi triangolari parziali |
| Esempio di calcolo con due carichi triangolari parziali | |