|
|
|
Sollecitazioni in un arco parabolico a tre cerniere originate da due carichi triangolari.
|
|
|
Calcolo delle reazioni vincolari
Le risultanti dei due carichi valgono rispettivamente
![]()
![]()
Per l’equilibrio orizzontale è
HA = HB
Scrivendo le equazioni cardinali della statica, riferite alla struttura completa, si ottiene
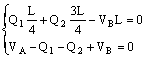
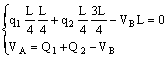
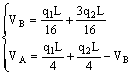
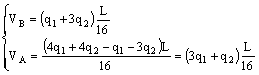
Per il calcolo delle reazioni orizzontali è necessario il ricorso all’equazione ausiliaria, scritta per metà struttura, imponendo l’azzeramento della sommatoria dei momenti
![]()
![]()
![]()
Sollecitazioni nella sezione generica posta alla distanza x dalla cerniera sinistra
|
|
Il carico qx relativo alla sezione posta alla distanza d può essere determinato scrivendo la relazione di similitudine
La risultante del carico parziale Qx vale pertanto
|
|
|
Nel tratto di struttura con guardando verso sinistra, si ha
Si ottiene quindi
Il momento è dato da
|
|
|
Nel tratto di struttura con guardando verso destra, si ha
Si ottiene quindi
Il momento è dato da
|
|
|
Nel tratto di struttura con
guardando verso sinistra, si ha
Si ottiene quindi
Il momento è dato da
|
|
|
Nel tratto di struttura con
guardando verso destra, si ha
Si ottiene quindi
Il momento è dato da
|
Nelle espressioni precedenti è
![]()
con la misura presa in valore assoluto.
| Argomenti correlati | |
| Lo studio geometrico di un arco parabolico | Sollecitazioni con due carichi uniformi |
| Proprietà delle funzioni iperboliche | Esempio di calcolo con due carichi uniformi |
| Caratteristiche geometriche di un arco parabolico | Sollecitazioni con peso proprio |
| Normativa per il calcolo del carico di neve su un arco parab. | Esempio di calcolo con peso proprio |
| Esempio di calcolo del carico di neve su un arco parabolico | Esempio di calcolo con due carichi triangolari |
| Sollecitazioni con un carico uniforme parziale | Sollecitazioni con due carichi triangolari parziali |
| Esempio di calcolo con un carico uniforme parziale | Esempio di calcolo con due carichi triangolari parziali |
| Scarica il foglio elettronico arcparab.zip (106 Kb) | |