|
|
L’equazione generale della parabola
si trasforma come precisato nel seguito, in relazione ai due riferimenti cartesiani in figura aventi origine degli assi rispettivamente nei punti A e C. |
Caratteristiche geometriche di una struttura ad arco parabolico.
|
|
L’equazione generale della parabola
si trasforma come precisato nel seguito, in relazione ai due riferimenti cartesiani in figura aventi origine degli assi rispettivamente nei punti A e C. |
Origine degli assi in A.
Questo prima sistema di riferimento è più funzionale al tracciamento dei diagrammi delle sollecitazioni.
La parabola passa per l’origine: c = 0.
Per x = L deve essere y = 0
Per x = L/2 deve essere y = f
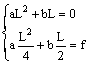
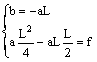
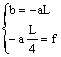
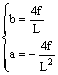
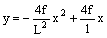
La tangente condotta per un generico punto D di ascissa x forma con l’asse delle ascisse un angolo w la cui tangente è pari alla derivata prima della funzione calcolata in tale punto.
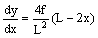
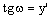
Origine degli assi in C.
Questo secondo sistema di riferimento si rivela maggiormente utile per il calcolo della lunghezza e della posizione del baricentro di singoli tratti di struttura.
La parabola passa per l’origine degli assi: b = c = 0
Per x’ = L/2 deve essere y’ = f
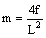
Per una parabola avente il vertice coincidente con l’origine degli assi di riferimento sono disponibili le seguenti espressioni, utili per il calcolo della lunghezza del tratto generico AB e per la determinazione della posizione orizzontale del suo baricentro.
|
|
Lunghezza dell’arco AB
Momento statico dell’arco AB
Ascissa del baricentro dell’arco AB |
| Argomenti correlati | |
| Lo studio geometrico di un arco parabolico | Sollecitazioni con due carichi uniformi |
| Proprietà delle funzioni iperboliche | Esempio di calcolo con due carichi uniformi |
| Normativa per il calcolo del carico di neve su un arco parab. | Sollecitazioni con peso proprio |
| Esempio di calcolo del carico di neve su un arco parabolico | Esempio di calcolo con peso proprio |
| Sollecitazioni con un carico uniforme parziale | Sollecitazioni con due carichi triangolari |
| Esempio di calcolo con un carico uniforme parziale | Esempio di calcolo con due carichi triangolari |
| Scarica il foglio elettronico arcparab.zip (106 Kb) | Sollecitazioni con due carichi triangolari parziali |
| Esempio di calcolo con due carichi triangolari parziali | |