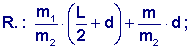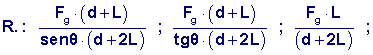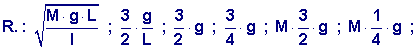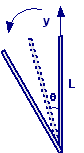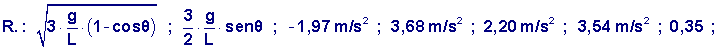Fisica

      

 

Costanti Fisiche

Unità Misura

Esercizi Fisica

Applet Java

 Test

Quesiti

  
 

Momento                                        

 
               
 

Esercizio n. 1

            
 

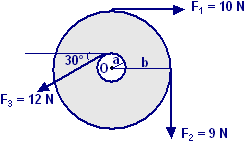
Trovare il momento risultante sulla ruota in figura, rispetto all’asse passante per O, se a = 10 cm e b = 25 cm.

  
 

R.: – 3,55 N∙m ;

 

  
               
 

Esercizio n. 2

            
 

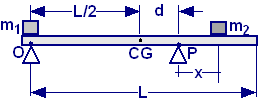
Una barra uniforme di massa m e lunghezza L supporta due blocchi di massa m1 ed m2 in due posizioni, come in figura.

La barra resta in equilibrio sul filo di due coltelli.

Per quale valore di x la barra sarà in equilibrio in P in modo che la forza normale in O sia zero?

  
 

 

  
               
 

Esercizio n. 3

            
 

Un’insegna uniforme che pesa Fg ed ha larghezza 2∙L è appesa a una barra orizzontale leggera, imperniata al muro e sostenuta da un cavo come in figura. Determinare:
a)  La tensione del cavo.
b)  Le componenti della forza di reazione esercitata dalla parete sulla barra in funzione di Fg , d , L , θ.

  
 

 

  
               
 

Esercizio n. 4

            
 

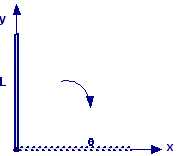
Una barra uniforme di lunghezza L e massa M è imperniata su un asse orizzontale privo di attrito passante per un suo estremo.

La barra è rilasciata da ferma in posizione verticale. Nell’istante in cui la barra è in posizione orizzontale, trovare.
a)  La sua velocità angolare.
b)  Il modulo della sua accelerazione angolare.
c)  Le componenti x ed y dell’accelerazione del suo centro di massa.
d)  Le componenti della forza di reazione del perno.

  
 

 
               
 

Esercizio n. 5

            
 

Una sbarretta sottile, di massa M e lunghezza L, è inizialmente ferma e poggiata su un piano scabro. Inizia a cadere col punto di contatto bloccato dall’attrito. Quando la sbarretta forma un angolo θ di 30° con la verticale, l’estremo a contatto col piano comincia a scivolare. Calcolare:
a)  In funzione di θ, per θ < 30° , la velocità angolare e l’accelerazione angolare della sbarretta.
b)  Per θ = 30°, l’accelerazione radiale e tangenziale del centro di massa della sbarretta.
c)  Per θ = 30°, le componenti orizzontale e verticale dell’accelerazione del centro di massa.
d)  Il coefficiente di attrito statico.

  
 

 
               
 

Esercizio n. 6

            
 

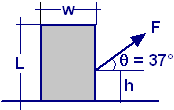
Una forza F agisce su un contenitore uniforme rettangolare di dimensioni L = 1 m e w = 60 cm, che pesa P = 400 N, come riportato in figura.
a) Se il contenitore scivola con velocità costante quando F = 200 N ed h = 0,400 m, trovare il coefficiente di attrito dinamico e la posizione della forza normale risultante.
b) Se F = 300 N, trovare il valore di h per il quale il contenitore inizia appena a ribaltarsi.

  
 

R.: 0,571 ; 50,1 cm ;

  
               
 

Esercizio n. 7

            
 

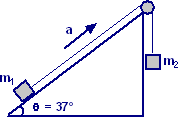
Due blocchi di massa m1 = 15 kg ed m2 = 20 kg posti come in figura, su di un piano inclinato, che forma un angolo θ = 37° con l’orizzontale, sono collegati da una fune di massa trascurabile, che passa su una carrucola di raggio R = 0,250 m e momento d’inerzia I.

Il blocco posto sul piano inclinato si muove verso l’alto con un’accelerazione costante a = 2 m/s2. Si determinino:
a)  Le tensioni T1 e T2 nei due tratti della fune.
b)  Il momento d’inerzia della carrucola.


  
 

R.: 118,5 N ; 156 N ; 1,17 kg/m2 ;

  
               
 

Esercizio n. 8

            
 

Una donna, la cui massa m = 60 kg, sta sul bordo di una piattaforma rotante orizzontale di momento d’inerzia  Ip = 500 kg∙m2  e  raggio R = 2 m. Il sistema è inizialmente fermo e la piattaforma può ruotare senza attrito intorno ad un asse fisso verticale passante per il suo centro. La donna si sposta successivamente lungo il bordo in senso orario ad una velocità costante rispetto al suolo vd = 1,5 m/s.
a)  In quale verso e con quale velocità angolare ruoterà la piattaforma?
b)  Quanto lavoro ha dovuto fare la donna per mettere in moto il sistema?

  
 

R.: 0,36 rad/s ; 99,9 J ;

  
               
 

Esercizio n. 9

            
 

Il disco circolare omogeneo riportato in figura ha una massa M = 6,5 kg ed un diametro D = 80 cm.

Si calcoli il suo momento d’inerzia rispetto ad un asse perpendicolare al disco passante per il punto G e per il punto A.

  
 

R.: 0,52 kg∙m2 ; 0,83 kg∙m2 ;

  
               
 

Esercizio n. 10

            
 

Come mostra la figura, una sfera solida omogenea rotola su una superficie orizzontale con velocità v = 20 m/s e successivamente risale il piano inclinato. Nel caso in cui le perdite dovute all’attrito siano trascurabili, quale sarà il valore di h nel punto in cui la sfera si ferma?

  
 

R.: 28,57 m ;

  
               
 

Esercizio n. 11

            
 

Un disco possiede un momento d’inerzia I = 0,0150 kg∙m2 e ruota a velocità ω = 3 giri/s. Un rivolo di sabbia cade sul disco ad una distanza d = 20 cm dall’asse di rotazione, formando un anello di raggio 20 cm. Quanta sabbia deve cadere sul disco per ridurre la velocità ad ω = 2 giri/s?

  
 

R.: 0,19 kg ;

 
               
 

Esercizio n. 12

            
 

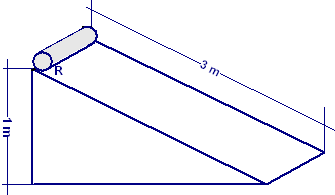
Un rullo cilindrico pieno di massa M e raggio R scende rotolando lungo un piano inclinato di lunghezza L = 3 m e di altezza h = 1 m.

Si determini il tempo Δt di discesa, trascurando gli attriti e la resistenza dell’aria.

  
 

R.: 1,66 s ;

 
               
 

Esercizio n. 13

            
 

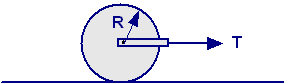
Un rullo cilindrico pieno, di massa M e raggio R, viene fatto scorrere su di un piano orizzontale mediante l’applicazione di una forza traente T. Si dimostri che per imprimergli una accelerazione costante pari a 2/3∙g è necessario che la forza traente T sia uguale al peso P del rullo stesso, trascurando l’attrito e la resistenza dell’aria.

  
 

R.: T = P ;

 
               
 

Esercizio n. 14

            
 

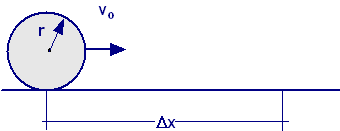
Un sfera omogenea, di raggio r e massa m, rotola su di un piano orizzontale.

Determinare lo spazio percorso dalla sfera a partire dall’istante in cui essa ha velocità di traslazione vo fino a quando essa si ferma, supponendo che la resistenza totale al rotolamento sia R.

  
 

 
               
 

Esercizio n. 15

            
 

Si abbia un disco omogeneo (puleggia), di raggio R e massa M, che può ruotare intorno al suo asse disposto orizzontalmente, senza attrito. Su di esso sia disposto un filo inestensibile che alle sue estremità porta due masse (m1 > m2). Lasciando il disco libero di ruotare la massa m1 si muove verso il basso con una accelerazione verticale a, mentre la massa m2 si muove verso l’alto con una accelerazione –a. Si determini a.

  
 

 
               
 

Esercizio n. 16

            
 

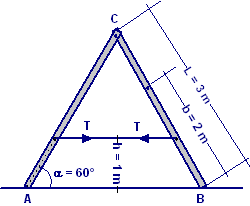
Una scala a doppio rampante è caricata da una massa m = 80 kg di un uomo nel punto indicato in figura. Si calcoli il valore della tensione T sul cavo di collegamento MN e la posizione dell’uomo che determina la tensione massima del cavo. Si supponga che il piano di appoggio sia senza attriti.

  
 

R.: 245,3 N ; 367,9 N ;

 
               
 

Esercizio n. 17

            
 

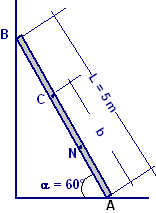
Una scala AB lunga L = 5 m è appoggiata in A sul pavimento ed in B sulla parete formando un angolo α = 60° con l’orizzontale.

Si chiede fino a quale punto C della scala può salire un operaio, la cui massa M = 75 Kg e che reca sulle spalle un carico m = 25 kg senza che la scala scivoli. Si chiede inoltre il valore del coefficiente di attrito per il quale la scala sia tutta percorribile.

Si trascuri la massa della scala. Il coefficiente di attrito tra la scala ed il pavimento e tra la scala e la parete sia μ = 0,35.

  
 

R.: 3,25 m ; 0,577 ;

 
               
 

Esercizio n. 18

            
 

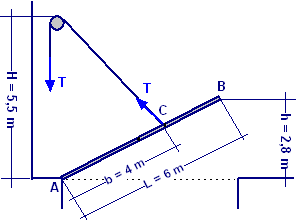
Sia dato il ponte levatoio schematizzato in figura. Si chiede quale deve essere lo sforzo di tensione T che deve essere applicato sul cavo di manovra per tenere sollevato l’estremo mobile B ad un’altezza h = 2,80 m sul livello della sponda destra. Il punto di ancoraggio C del cavo al ponte dista da A della quantità b = 4 m e la lunghezza totale del ponte è L = 6 m. L’altezza del perno della carrucola (il cui raggio si ritiene trascurabile) è H = 5,50 m. La massa del ponte è M = 150 kg e si suppone applicata alla mezzeria del ponte stesso.

Si trascuri l’attrito.

  
 

R.: 1013 N ;

 
               
 

Esercizio n. 19

            
 

Una barretta cilindrica sottile di massa m = 300 g e lunghezza h = 2,8 m è imperniata, senza attrito, in un punto ad ¼ della sua lunghezza ed è inizialmente ferma in posizione orizzontale.
Successivamente  la barretta  viene  lasciata  libera e, quando si trova  in posizione  verticale, urta  contro un  blocco di  massa M = 7 kg che è inizialmente fermo su di un piano orizzontale privo di attrito.
Si determini la velocità con cui si muove il blocco dopo l’urto che si suppone sia perfettamente elastico.


 
 

R.: 0,16 m/s ;

 
     
 

Esercizio n. 20

            
 

Una barretta di lunghezza d = 50 cm e massa, uniformemente distribuita, M = 1,0 kg è incernierata ad un estremo e può ruotare liberamente rispetto ad un asse orizzontale.
Un proiettile puntiforme di massa m= 100 g colpisce orizzontalmente la bacchetta ad una distanza h = 30 cm dalla cerniera.

Il proiettile, dopo l’urto, cade verticalmente; se la barretta devia di un angolo θ = 28° si determini la velocità del proiettile prima dell’urto.

  
 

R.: 7,29 m/s ;