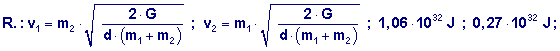Fisica

      

 

Costanti Fisiche

Unità Misura

Esercizi Fisica

Applet Java

 Test

Quesiti

  
 

La gravitazione                                       

 
               
 

Esercizio n. 1

            
 

La massa ed il raggio della terra e della luna sono MT = 5,98·1024 kg, RT = 6,37·106 m, ML = 7,36·1022 kg, RL = 1,75·106 m, rispettivamente. La loro distanza relativa è d = 3,84·108 m.

Spiegare come mai è necessario più carburante ad una navicella per viaggiare dalla terra alla luna che non per il viaggio di ritorno. Stimare la differenza.

  
 

R.: 23 ;

  
               
 

Esercizio n. 2

            
 

Il campo gravitazionale sulla superficie della luna è circa un sesto di quello sulla superficie terrestre. Se il raggio della luna è circa un quarto di quello della terra, trovare il rapporto la densità media della luna e la densità media della terra.

  
 

R.: 2/3 ;

 
               
 

Esercizio n. 3

            
 

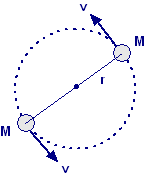
Due stelle di massa M ed m, poste a distanza d, ruotano in orbite circolari attorno al loro centro di massa. Mostrare che ogni stella ha un periodo dato da:

  
 

R.:

  
               
 

Esercizio n. 4

            
 

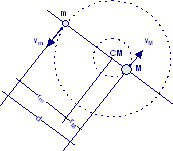
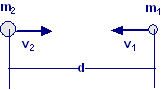
Due ipotetici pianeti di massa m1 ed m2 e raggi r1 ed r2 rispettivamente, sono fermi quando sono separati da una distanza infinita.

A causa della loro attrazione gravitazionale, essi vanno l’uno verso l’altro su una retta di collisione.

Supposto m1 = 2,00·1024 kg, m2 = 8,00·1024 kg, r1 = 3,00·106 m ed r2 = 5,00·106 m.

Quando la distanza fra i loro centri è d, calcolare la velocità di ciascun pianeta e la loro velocità relativa.

Calcolare l’energia cinetica di ciascun pianeta appena prima della collisione.

 

  
 

 
               
 

Esercizio n. 5

            
 

Un sistema binario di stelle ruota circolarmente attorno al comune centro di massa a metà strada tra esse. Ciò significa che la massa delle due stelle è uguale. Se la velocità orbitale di ciascuna di esse è v = 220 km/s ed il periodo orbitale di ciascuna è 14,4 giorni, trovare la massa M di ciascuna stella.

  
 

R.: 1,26·1032 kg ;

  
               
 

Esercizio n. 6

            
 

Io, una piccola luna di Giove, ha un periodo orbitale di 1,77 giorni ed un raggio orbitale r = 4,22·105 km.

Determinare la massa M di giove.

  
 

R.: 1,90·1027 kg ;

  
               
 

Esercizio n. 7

            
 

Determinare la velocità con cui va lanciato dalla superficie della terra un satellite che si vuole porre in orbita geostazionaria e la velocità del satellite quando sarà in orbita. Si consideri nulla la resistenza offerta dall’atmosfera e trascurabile ogni effetto dovuto alla rotazione della terra ed  all’influenza degli altri corpi celesti.

(Si ricordi che un satellite in orbita geostazionaria risulta fermo rispetto alla terra.)

G = 6,67·10–11 N·m2·kg–2 , MTERRA = 5,98·1024 kg , RTERRA = 6,37·103 km.

  
 

R.: 10,76 km/s ; 3,07 km/s ;

  
               
 

Esercizio n. 8

            
 

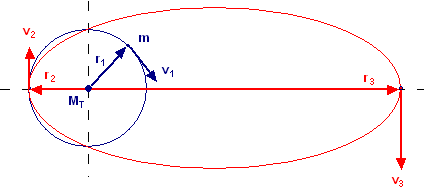
Un’astronave ruota inizialmente intorno alla Terra su un’orbita circolare di raggio r1 = 6500 km.

Successivamente, dopo aver acceso i motori per un brevissimo intervallo di tempo, l’astronave acquista una velocità v2 tale da portarla sull’orbita ellittica mostrata in figura.

I vertici vicino e lontano di tale orbita hanno distanza dal centro della Terra ( MT = 6.0·1024 kg ) pari a r2 = r1 e r3 = 30000 km.

Determinare:

a)  la velocità v1 dell’astronave mentre percorre l’orbita circolare iniziale.

b)  le velocità v2 e v3 dell’astronave quando si trova nei vertici vicino e lontano dell’orbita ellittica.

  
 

R.: 1,01·104 m/s ; 2,18·104 m/s ;