|
|
Tutti gli appunti |
 |
RICHIAMI SULLE CURVE ALGEBRICHE
Determinazione dei parametri caratteristici |
 |
|
| ||
| Prima parte |
CONICHE Proprietà generali
Richiami delle curve algebriche piane – polinomio caratteristico - curve algebriche irriducibili – ordine di
una curva algebrica – punti di intersezione con una retta – studio locale di una curva algebrica – punti semplici –
espressione della retta tangente – punti multipli - curva algebrica in coordinate omogenee e retta tangente
espressa con le derivate parziali – teorema di Bezout. |
|
| Seconda parte |
Conseguenze dell’intersezione di una conica con la retta impropria – discriminante caratteristico – ellisse, iperbole, parabola – coniche degeneri – diametri e centro di una conica – diametri: polari di punti impropri – centro: intersezione di diametri – centro proprio al finito: ellisse iperbole (coniche a centro) – centro all’infinito, sulla retta impropria: parabola – diametri coniugati e loro costruzione – condizione di coniugio tra due diametri – diametri autoconiugati – asintoti – condizione di autoconiugio – Condizione di autoconiugio di un asintoto – determinazione asintoti, come polari dei punti impropri – equazioni canoniche delle coniche a centro: ellisse iperbole – tipi di coniche a centro con assi di riferimento due diametri coniugati – equazione canonica della parabola – diametri traversi e non traversi. |
|
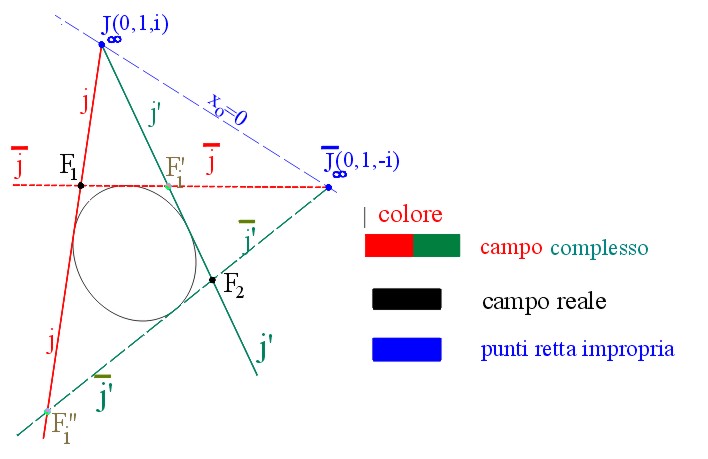
| Terza parte | Assi della conica – vertici – assi delle coniche a centro – condizione dei parametri direttori degli assi – asse della parabola – richiami sugli elementi geometrici nel campo complesso – punti complessi: proprietà – rette complesse: proprietà – punti ciclici rette isotrope – fuochi delle coniche: ottenuti dalle quattro intersezioni tra le rette isotrope, tangenti alla conica, condotte dai due punti ciclici J(0,1,i), J’(0,1,-i) – coniche a centro – parabola – direttrici delle coniche: polari dei fuochi – eccentricità – proprietà delle coniche con fuoco e direttrici assegnati – tipo di conica dipende dal valore dell’eccentricità |
|
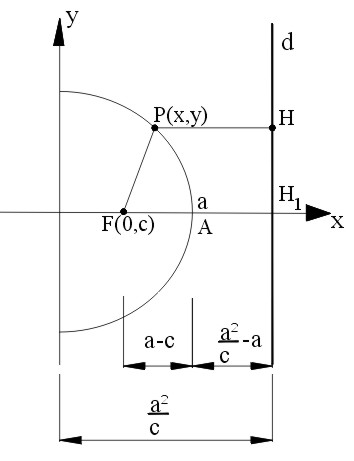
| Quarta parte | determinazione degli elementi con i metodi generali Determinazione degli elementi dell’ellisse espressa in forma canonica: con a>b e a<b – centro: intersezione di due diametri, polari di I(0,1,0) e I’(0,0,1) – assi: diametri coniugati ortogonali – vertici – fuochi: intersezioni tra rette isotrope, tangenti alla conica, condotte dai due punti ciclici J(0,1,i), J’(0,1,-i) – due fuochi reali e due complessi coniugati – direttrici: polari dei fuochi – eccentricità – forma dell’ellisse e valori dei parametri caratteristici in base all’eccentricità: posizione dei fuochi e delle direttrici – ellisse come luogo geometrico – determinazione degli elementi dell’iperbole espressa in forma canonica: centro – assi – fuochi – direttrici – eccentricità – asintoti: polari dei punti impropri. |
|
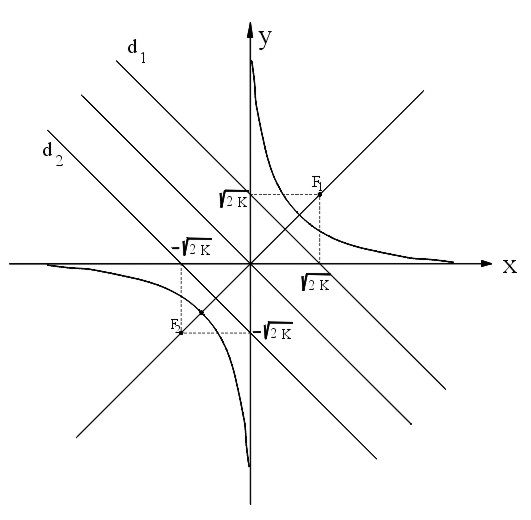
| Quinta parte | Iperbole come luogo geometrico – iperbole equilatera con gli assi cartesiani coincidenti con gli asintoti – rotazione degli assi - determinazione degli elementi: fuochi, vertici, assi, direttrici - Studio con procedimento generale dell’iperbole equilatera nella forma generica – determinazione con i metodi generali degli elementi: centro – assi – vertici – asintoti – fuochi - direttrici |
|

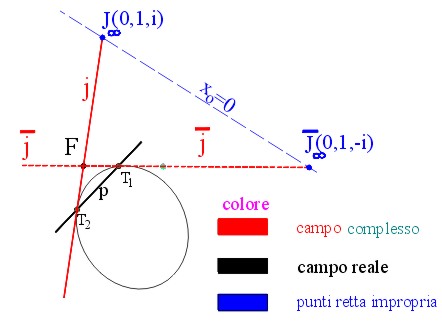
| Sesta parte | e FUNZIONE RAZIONALE DI SECONDO GRADO
Matrice caratteristica – punto improprio della parabola – centro della parabola - Asse della parabola –
vertici della parabola – fuochi della parabola: intersezioni tra rette isotrope, tangenti alla conica, condotte
dai due punti ciclici J(0,1,i), J’(0,1,-i) – direttrice della parabola – parabola come luogo
geometrico – studio della parabola come funzione razionale intera di secondo grado: determinazione
con i metodi generali di: centro, assi, vertici, fuoco reale finito, direttrice. |
| |
SERAFO | APPUNTI | FRESCACCE | CENE | IL RITORNO |