Elementi di filosofia naturale

Parte Prima: Principi per una fisica moderna
di Roberto Monti (1984)

Fonte: R. Monti, "Scritti di critica alla Teoria della Relatività (1984-1987)"

Ed. Andromeda, Roma 2018

A cura [ndc] di Nereo Villa

Indice: Prefazione - Determinazione della conducibilità elettrica dello spazio di fondo - Il paradosso di Olbers e la radiazione di fondo - La velocità della luce - Conclusione.

Prefazione
 

Spazio tempo e causalità sono le categorie razionali primarie di ogni interpretazione qualitativa del mondo fisico; di ogni ulteriore articolazione dell'esperienza dalla quale sono indotte. Ciascuna delle loro varie, possibili, specificazioni operazionali, una volta definita, costituisce il fondamento di ogni interpretazione quantitativa.

 
In altri termini: il "metodo della scienza", proprio in quanto esistono varie, possibili interpretazioni quantitative del mondo fisico (varie, possibili, forme di sistematizzazione della conoscenza), non esiste; ma i suoi "confini razionali" (spazio, tempo, causalità), sì.

 
Denominerò conseguentemente l'insieme di queste affermazioni: "Principio di razionalità".

Verso la fine del XIX secolo le briciole dei segni che secoli disattenti avevano lasciato accumulare sulla spiaggia della conoscenza, così abbondanti quando per primi Galileo e Newton tornarono a percorrerla, non bastano più per appagami di uno sguardo a questo oceano.

 
Agli inizi del XX secolo è tempo, per Einstein, di "fare ipotesi". Ma la Relatività einsteiniana, pur riconoscendo la distinzione tra le categorie di spazio e tempo e le loro specificazioni, presuppone di poter costituire interpretazioni qualitative e quantitative che prescindono dalla causalità come categoria e specificazione della categoria.

Al di fuori, in altri termini, del "principio di razionalità". Ne risulta una serie di paradossi che degenerano via via fino a configurare la teoria stessa come un limite intollerabile ad ulteriori sviluppi; il suo superamento, conseguentemente, come obiettivo necessario della fisica moderna, ancora una volta è il tempo di "fare ipotesi".

 
(Questa serie di articoli era stata originariamente concepita per il 3° numero di Autonomia Proletaria; vedi: Autonomia Proletaria n. 2, Novembre 1980, pag. 95. Alcune spiacevoli circostanze mi hanno imposto, come è evidente, un ritardo imprevisto).

È opinione comune, tra i fisici contemporanei, che la relatività ristretta einsteiniana sia "una teoria sperimentalmente ben fondata". In realtà tutte le "leggi sperimentalmente ben fondate" impropriamente attribuite ad Einstein erano già note prima del 1905 [1], mentre i postulati della relatività ristretta, sulla base dei quali Einstein fu in grado di giungere ad una deduzione di queste leggi, erano - e sono - ben lungi dall'essere "sperimentalmente ben fondati".

Ma vediamo le cose più da vicino.

Elettricità e magnetismo si presentano in natura separatamente, e separatamente furono esaminate.

Per ciascuna delle interazioni elettrostatica e magnetostatica Coulomb determinò una legge di tipo newtoniano.

Ampere stabilì poi la relazione dimensionale: P = Q · velocità.

(P = polo magnetico o intensità polare; Q = carica elettrica) che indusse a non considerare P come quinta dimensione indipendente e, conseguentemente, all'adozione del sistema a quattro unità MKSQ [2]. In tale sistema le leggi risultanti dai vari esperimenti relativi ai campi elettrici e magnetici nello "spazio assolutamente in quiete" sono state riassunte nelle seguenti equazioni (Maxwell):
 

div(ε₀E) = ρ                rot E = - ∂ (μ₀H)/r

(1)

div(μ₀E) = 0                rot H = (ε₀· ∂/∂r + σ₀) E 

Ove

[∂ = derivata parziale - ndc]

E = intensità del campo elettrico;

H = intensità del campo magnetico;

ρ = densità di carica elettrica;

ε₀ = permettività elettrica dello spazio;

μ₀ = permeabilità magnetica dello spazio;

σ [mancante nel testo - ndc] = conducibilità elettrica dello spazio;

r = "tempo proprio" dello "spazio assolutamente in quiete".

In assenza di cariche elettriche (ρ = 0) le equazioni (1) forniscono, per E e per H, le equazioni:

ε₀μ₀ · ∂²E/∂r² + σ₀μ₀· ∂E/∂r = ΔE

(2)

ε₀μ₀ · ∂²H/∂r² + σ₀μ₀· ∂H/∂r = ΔH

Il valore della grandezza c₀ = (velocità delle onde elettromagnetiche) risultò avere lo stesso ordine di grandezza della velocità (cinematica) della luce c_M = λ₀ . Di conseguenza Maxwell interpretò la luce come un fenomeno elettromagnetico [3].
 

Alcune "asimmetrie" nell'elettrodinamica di Maxwell che non appaiono essere aderenti ai fenomeni... come pure i falliti tentativi di constatare il moto della terra relativamente al mezzo luminoso" [4], indussero Einstein a formulare una teoria alternativa fondata su due postulati.

Il primo postulato ("Principio di relatività") afferma che "per tutti i sistemi di coordinate per i quali valgono le equazioni della meccanica, debbono anche valere le stesse leggi elettrodinamiche ed ottiche", e da questo principio discende la successiva affermazione secondo cui: "l'introduzione di un etere luminifero è superflua... né verrà introdotto uno 'spazio assolutamente in quiete' corredato di particolari proprietà" [4].

Il secondo postulato, secondo Einstein "solo apparentemente incompatibile col precedente", afferma infine che "la luce nello spazio vuoto si propaga con una velocità determinata V indipendente dalla velocità del corpo emittente".

A questo postulato segue "per definizione" l'affermazione secondo cui "il tempo che a luce impiega in qualsiasi percorso di sola andata è uguale al tempo che essa impiega nel corrispondente percorso di ritorno" e, come ovvia conseguenza, il "fatto" che "la velocità della luce ha, nella nostra teoria, fisicamente il ruolo di una velocità infinita" [4].

Cominciamo con l'osservare che, paradossalmente, nelle equazioni delle onde maxwelliane (2), valide "esattamente" in un sistema di riferimento solidale con lo "spazio assolutamente in quiete" corredato delle "particolari proprietà" ε₀ , μ₀ , σ₀ , solo quest'ultima (la conducibilità elettrica), conformemente al "principiò di relatività" (primo postulato), viene posta definitivamente ed arbitrariamente uguale a zero; mentre il tempo proprio T dello "spazio assolutamente in quiete" (che chiamerò da ora in avanti "spazio di fondo"), viene sostituito da un generico "tempo locale" t, ed esse divengono:

ε₀μ₀ · ∂²E/∂r²  = ΔE

(2')

ε₀μ₀ · ∂²H/∂r² = ΔH

Per di più Einstein non specifica, inizialmente (secondo postulato), di quale "velocità V" stia parlando, e mostra con ciò di ignorare la distinzione tra misure elettromagnetiche e cinematiche della "velocità della luce", così come i dati sperimentali ad esse relativi; mentre subito appresso adotta come "costante della teoria di Maxwell" la definizione cinematica di

V (c_M = 2ΔL/ΔT = λυ)

in luogo della corretta "velocità elettromagnetica" c₀ =

ponendo con ciò, arbitrariamente, l'ipotesi: c₀ = c_M [4].

Assume poi "valido per definizione" un risultato sperimentalmente non verificato dal quale consegue il grossolano paradosso secondo cui: "una velocità finita è infinita". Ora, se il primo postulato può rientrare nell'ambito delle possibilità connesse all'esistenza di "uomini senza adeguate capacità di riflettere su problemi scientifici" [5], i dati sperimentali disponibili fino al 1905 [6] indicavano l'esistenza di una discrepanza tra c₀ e C_M; e cioè che la sostanza del secondo postulato einsteiniano, e quindi la sostanza dell'intera teoria [7], non poteva ritenersi sperimentalmente fondata.

In altri termini: la teoria della relatività speciale einsteiniana richiedeva, per risultare sperimentalmente fondata, che fossero verificate le identità:

1) σ₀ = 0 (primo postulato. Questa identità comporta anche la relazione: R_D = ∞; ove: R_{D =} rigidità dielettrica dello spazio di fondo. Si noti che, a rigor di logica, il primo postulato richiede, oltre alla: σ₀ = 0, anche le identità: ε₀ = 0, μ₀ = 0);

 

2) c₀=c_M (secondo postulato).

Se la prima identità, per quanto cozzi violentemente contro un "buon senso" stratificatosi non già "nei primi 18 anni della nostra esistenza" [8], ma nel corso di millenni di sperimentazione del mondo fisico, era - ed è - completamente arbitraria, la seconda era - ed è - ben lungi dall'essere sperimentalmente verificata ad un livello di incertezza tale da poterla ritenere necessariamente valida. È lecito quindi esaminare quali siano le conseguenze implicite nelle ipotesi:  σ₀≠0 e c₀≠c_M. E a questo proposito si noti innanzitutto che in tali ipotesi, sostituendo il termine "spazio vuoto" con "spazio di fondo" (negazione del primo postulato einsteiniano), e V con c_0, il secondo postulato diviene sostanzialmente e formalmente corretto.

La teoria alternativa a quella einsteiniana che intendo qui esporre è fondata, appunto, sull'unico, seguente, postulato: ''Le onde ettromagnetiche si propagano, nello spazio di fondo, con velocità

c₀ = indipendente dalla velocità del corpo emittente".

 

 

Indice: Prefazione - Determinazione della conducibilità elettrica dello spazio di fondo - Il paradosso di Olbers e la radiazione di fondo - La velocità della luce - Conclusione.

Determinazione della conducibilità elettrica dello spazio di fondo
 

Data la sostanziale arbitrarietà dell'ipotesi σ₀≠0 non resta che ricercare i modi attraverso i quali il suo valore può essere determinato sperimentalmente.
 

Il primo è fornito, a livello microcosmico, dalla relazione:
 

E = 1/σ₀ ∙ J                                                                                          (3)

(J = densità di corrente)

Infatti l'intensità di campo elettrico che determina un passaggio di corrente (sottoforma di creazione di coppie e⁺, e^-) attraverso il dielettrico "spazio di fondo": o, in altri termini, la rigidità dielettrica dello spazio di fondo R_D , può essere facilmente calcolata come segue:

2m_ec₀² = ½ε₀E² ∙ 4π/3 ∙ 2r₀r₀²  →

                                                                                                              (4)

|E| = R_D = √3m_ec₀²/2πε₀r₀³ 4 ∙ 10²⁰  V/m

ove: m_e = massa a riposo dell'elettrone (positrone); c₀ = velocità della luce; ε₀ = permittività elettrica dello spazio di fondo; r₀ = "raggio classico" dell'elettrone.

Fig. 1. Creazione di una coppia e⁺, e^- nello spazio di fondo.

E = campo elettrico; r₀ = raggio classico dell'elettrone (positrone).
 

Intensità di quest'ordine di grandezza possono realizzarsi, come è noto, in prossimità dei nuclei degli elementi superpesanti prodotti dagli acceleratori di ioni pesanti [9]. La densità di corrente risultante dal cosiddetto "decadimento del vuoto" che deve verificarsi nelle immediate vicinanze di questi sistemi artificiali costituisce, infine, il secondo fattore che, nella relazione:

E = 1/R_D | J |                           (5)

consente di valutare la grandezza σ_{0 .}
 

Ma di questo fenomeno sembra provata unicamente, al momento, l'esistenza [10]. L'attuale stato delle nostre conoscenze non consente, dunque, la misura della grandezza σ₀ a livello microcosmico.

Diversa, al contrario, è la situazione a livello macrocosmico.
 

Infatti le equazioni (2), nell'ipotesi: E=E(x,τ); H=H(x,τ) divengono un caso particolare dell'"equazione dei telegrafisti":
 

∂²Y/∂x² - CL ∂²Y/∂r² - (CR + AL) ∙ ∂y/∂τ - AB ∙ Y = 0                                  (6)

ove: C = capacità; L = induttanza; R = resistenza; A = dispersione per unità di lunghezza, di una linea di trasmissione infinita (cavo coassiale, guida d'onda).

Ponendo le seguenti corrispondenze:

C → ε₀ ; L → μ₀ ; R → 0 ; A → σ₀

l'equaziune (6) diviene:
 

∂²Y/∂x² - 1/c₀  (∂²Y/∂τ² + 1/T ∙ ∂y/∂r) = 0                                  (7)

ove: c₀ = ; T = ε₀/σ₀ (tempo di rilassamento).
 

La soluzione che ci interessa è la seguente:

Y = e^-δx g(x - c₀τ)

ove: δ = 1/2Tc₀ = σ₀/2ε₀c₀ = R₀σ₀/2 ; (R₀ = √1/μ₀ε₀ = "resistenza d'onda dello spazio di fondo" = 376,74 Ω).

Abbiamo dunque:

                             (8)

Sia: W₀ = h₀υ₀ energia iniziale di un fotone.

W₁ = h₀υ₁ energia residua dopo un percorso x.

(9)

Ora, i redshifts galattici possono, ovviamente, essere attribuiti allo smorzamento dell'energia delle onde elettromagnetiche emesse dalle varie galassie in moto causale entro un universo stazionario, nel quale una velocità di interazione gravitazionale υ₀>>c₀ , secondo Laplace [11], consente moti localmente coordinati di ammassi e superammassi di galassie; e i redshifts galattici z consentono di determinare la grandezza σ₀:

Si ha precisamente [APPENDICE A1]:

σ₀ = (2.85 ± 0,15) 10^-29 (Ω ∙ m)                      (10)

Le equazioni (6)-(10) consentono alcune considerazioni: a) Il modello che esse suggeriscono per la propagazione di un fotone nello spazio di fondo è il seguente: il fotone scava nello spazio di fondo una guida d'onda per la quale la dispersione superficiale è praticamente nulla, mentre nulla (<10^-29) è la resistenza R alla propagazione del segnale. La resistenza d'onda R₀ deve conseguentemente interpretarsi come una resistenza trasversale incontrata dalla corrente di spostamento del campo elettrico rapidamente variabile dell'onda elettromagnetica. Le questioni relative al significato fisico ed al livello di quantizzazione della corrente di spostamento sono, così, riaperte [12].

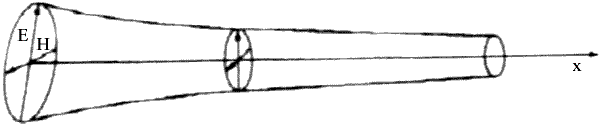
Fig. 2. "Guida d'onda" di un fotone. E = campo elettrico;

H = campo magnetico; x = direzione di propagazione.

b) Lo smorzamento è trascurabile per dimensioni dell'ordine della nostra galassia. L'equazione delle onde elettromagnetiche nel sistema di riferimento quasi-stazionario T (Terra):
 

1/c_M² ∙ ∂²E(H)/∂t² ; t = tempo terrestre

deve considerarsi un'approssimazione valida fino all'ordine decimale per il quale si ha: c₀ c_M
 

La semplice esistenza del termine: σ₀μ₀ ∙ ∂E(H)/∂t vanifica,come la questione della Lorentz-invarianza, ogni questione di invarianza dell'equazione delle onde elettromagnetiche (nella misura in cui, appunto, esistono sistemi di riferimento privilegiati: quelli solidali con lo spazio di fondo).
 

b) La cosiddetta "legge di Hubble" deve considerarsi erronea.

Voglio sottolineare a questo proposito come Burbidge abbia giustamente stigmatizzato il fatto che, contrariamente alla logica galileiana che dovrebbe informare la Fisica, "l'evidenza è messa in dubbio o ignorata e gli argomenti statistici criticati o derisi... poiché non disponiamo di una teoria che possa rendere conto naturalmente di un redshift non cosmologico... Opinioni che si credono saldamente fondate prevalgono al di sopra di un'evidenza ritenuta secondaria. Ciò conduce ad una reazione - l'evidenza è criticata e messa in dubbio, così che non viene fatto alcun serio tentativo di sviluppare nuove idee o teorie basate su di essa. Poiché non si lavora sui problemi, essi non vengono risolti e, per alcuni eminenti scienziati, l'assenza di una teoria costituisce prima facie evidenza contro l'ipotesi. E così vanno le cose!" [13].

Infatti il lavoro di Hawkins dapprima [14], il "sorprendente risultato" sottolineato da De Vaucouleurs in seguito [15] e, infine la sterile controversia tra le "scuole" di Sandage da un lato e di De Vaucouleurs dall'altro [16] avrebbero dovuto da lungo tempo ormai condurre a questa conclusione.

L'equazione (9) riguarda, ovviamente, l'intero spettro elettromagnetico e sostituisce l'erronea "legge di Hubble" che fornisce risultati inattendibili nel calcolo delle distanze e della luminosità totale dei "corpi celesti".

Supponiamo, ad esempio, di esaminare lo spettro di una galassia vicina come M31 (Andromeda). Un oggetto di questo genere, a una distanza di 5000, 10000, 20000, 40000, 80000 Mpc, fornirà una serie di immagini ciascuna delle quali deve essere "ricostruita".
 

Per x = 5000 Mpc abbiamo infatti:
 

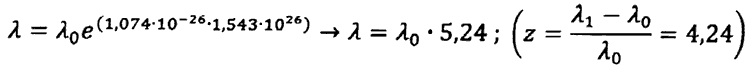
Per x = 10000 Mpc →λ = λ₀ 27,5
Per x = 20000 Mpc →λ = λ₀ 756,5

Per x = 40000 Mpc →λ = λ₀ 572321

Per x = 80000 Mpc →λ = λ₀ 3,27-10²¹

Infine, come è noto, quando z avvicina e poi supera l'unità, la legge di Hubble viene modificata come segue:

v = c₀z

viene sostituita da

v = c₀ ∙ (z+1)²-1/(z+1)²+1

mentre: c₀z = Hx diviene:

ove: H = 50, 100; q₀ = 0, ½, 1

(D. A. Schwartz, M. V. Zombeck, "Relazioni cosmologiche.

Memorandum". Centro di Astrofisica Harvard College Observatory.

Smithsonian Astrophysical Observatory. 16 Agosto 1979).

Così per un redshift z = 2 (x = 3300 Mpc) la legge di Hubble, nelle sue 6 versioni, fornisce:

e alla luminosità di un "oggetto celeste" di questo genere viene attribuito un valore da 3 a 53 volte superiore al suo valore reale.

Per z = 4 (x = 4850 Mpc) la legge di Hubble nelle sue 6 versioni fornisce:

x (50,0) = 71950 Mpc
x (50,½) = 33157 Mpc
x (50,1) = 23983 Mpc
x (100,0) = 35975 Mpc
x (100,½) = 16578 Mpc
x (100,1) = 11991 Mpc

e alla luminosità di un "oggetto celeste" di questo genere viene attribuito un valore da 6 a 220 volte superiore al suo valore reale.

E così via...

Indice: Prefazione - Determinazione della conducibilità elettrica dello spazio di fondo - Il paradosso di Olbers e la radiazione di fondo - La velocità della luce - Conclusione.

Il paradosso di Olbers e la radiazione di fondo

Nel 1823 Olbers sottolineò che, nell'ipotesi di un Universo infinito ed isotropo, entro il quale la distribuzione delle stelle e delle galassie (della "materia") sia simile a quella che si può osservare intorno a noi, il cielo dovrebbe essere sempre illuminato a giorno, mentre, al contrario, "di notte il cielo è buio" [17].

Nella stessa ipotesi la teoria dei campi di forza conduce, attraverso il teorema di Gauss, allo stesso risultato paradossale: un flusso di forza infinito, in contraddizione con l'evidenza sperimentale [18].

Entrambi questi paradossi possono essere facilmente spiegati nell'ipotesi: σ₀ = 0. Supponendo cioè - in contraddizione con il "principio di relatività" einsteiniano - l'esistenza di uno spazio di fondo "corredato di particolari proprietà" [Einstein, cfr. nota 4]. Infatti da tale ipotesi segue la necessità di introdurre un coefficiente di smorzamento tanto nelle equazioni delle forze quanto nell'espressione matematica di ogni tipo di radiazione.

Per ciò che riguarda le forze si tratta di estendere la modificazione della legge di Newton suggerita da Laplace e Seeliger [19] (successivamente adottata da Yukawa per le interazioni forti) alle interazioni deboli, elettrostatiche, magnetostatiche e, in generale ad ogni tipo di interazione.

Lo smorzamento dell'intensità del campo di forza sarà attribuito ovviamente, sulla base del principio di azione e reazione (terza legge di Newton), ad un "anti-campo di polarizzazione" determinato, nello spazio di fondo, dalla presenza di "cariche" (gravitazionali, deboli, elettriche magnetiche, forti, ecc.).

 
Si noti che in tale ipotesi il paradosso dell'autointerazione di una particella con il proprio campo scompare immediatamente: la particella non ha più "autointerazione", ma interagisce con lo spazio di fondo.

Qualsiasi forza F tra due cariche C_l e C₂ poste ad una distanza r l'una dall'altra diviene in altri termini funzione di due parametri; la permeabilità k e il coefficiente di smorzamento a dello spazio di fondo:

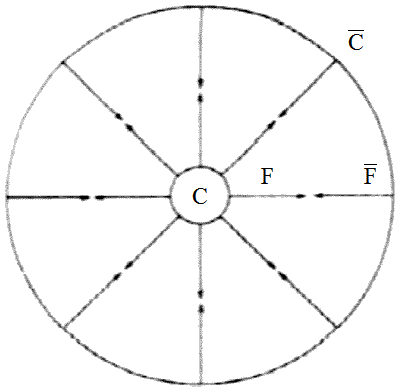
Fig. 3. La carica C induce, entro una sfera di raggio finito,

un'"anticarica di polarizzazione" C. Un "anticampo di

polarizzazione" si oppone al campo di forza F e annulla

questo campo entro una sfera di raggio finito.

Per ciò che riguarda infine l'energia di qualsiasi radiazione e in particolare della radiazione elettromagnetica, l'equazione (9) consente la seguente conclusione: di notte il cielo è "illuminato", ma non alle lunghezze d'onda e con l'intensità supposte da Olbers proprio in quanto esiste un coefficiente di smorzamento: R₀σ₀ = 1,074 ∙ 10^-26m^-1 .

In altri termini, la radiazione emessa dalle varie "sorgenti elettromagnetiche" subisce uno smorzamento; ed uno dei risultati di tale smorzamento è, per esempio, la "luminosità a 3°K" della radiazione di fondo generale.

Anche la lunghezza d'onda della radiazione più dura, infatti, dopo un percorso finito si riduce a microonde.

Nel caso, ad esempio, di γ duri ↔ λ₀ = 10^-13 m, abbiamo:

anni luce.
 

Possiamo immaginare, di conseguenza, che la radiazione di fondo generale risulti dai contributi delle sorgenti di radiazione elettromagnetica "locali" (Universo visibile) e dalle sorgenti di radiazione che non sono distinguibili dal fondo generale (Universo invisibile).

Per concludere: l'esistenza di una conducibilità elettrica dello spazio di fondo σ₀ ≠ 0; σ₀ = (2,85 + 0,15) ∙ 10^-29 (Ωm)^-1 costituisce la prima prova sperimentale contro il "principio di relatività" einsteiniano (primo postulato della teoria della relatività ristretta), ed una prova indiretta a sostegno dell'ipotesi: c₀ ≠ c_M le cui conseguenze passiamo ora ad esaminare.

Indice: Prefazione - Determinazione della conducibilità elettrica dello spazio di fondo - Il paradosso di Olbers e la radiazione di fondo - La velocità della luce - Conclusione.

La velocità della luce [citato in "La cintura di sicurezza (seconda puntata)" - ndc]

Ho affermato, nell'introduzione, che l'identità c₀ = c_M è ben lungi dall'essere verificata sperimentalmente ad un livello di incertezza tale da poterla ritenere necessariamente valida.

Infatti, mentre le misure cinematiche della velocità della luce c_M sono oggi realizzate con incertezze dell'ordine di 10^-9 e si ha: c = (299792458 ± 1) m/s [20], il valore medio della velocità "elettromagnetica" della luce c₀ , risultante dalle migliori misure effettuate fino al 1900 [21] era, con un'incertezza ritenuta non superiore a 1∙10³:c₀ = 30005000 ± 300000 m/s.

Dopo questa data una nuova misura di questa grandezza, l'ultima, fu effettuata da Rosa e Dorsey nel 1905-1907 [22] e fornì il risultato erroneo:

c₀ = 299710000 m/s; che fu corretto nel 1932 da N. E. Dorsey [23] in:
c₀ = 299790000 ± 40000 m/s; con un'incertezza supposta pari a 1,3∙10^-4 che non è tuttavia affidabile (Rosa e Dorsey, ad esempio, non presero in considerazione l'influenza dell'umidità atmosferica sulla permittività elettrica dell'aria, e così via).

La reale incertezza di queste misure di c₀ può dunque ritenersi non inferiore a 10^-3, e cioè dello stesso ordine di quelle effettuate fino al 1900: una serie che mostrava una discrepanza tra c₀ e c_M .

Dorsey concluse la sua relazione del 1932 sul risultato definitivo della misura effettuata nel 1905-1907 affermando che: "Grazie all'influenza di Einstein e delle teorie della relatività" l'identità c₀ = c_M  poteva essere accettata non tanto sulla base "dei risultati sperimentali che, lungi dall'essere trascurabili, sono stati completamente tralasciati, ma sulla base di considerazioni di natura filosofica" [in realtà si tratta della "filosofia" dell'"l'ha detto Einstein", divenuta una specie di password per il divieto a qualsiasi percezione e intuizione in merito; vedi a questo proposito "Sul bambino molto piccolo della relatività assoluta" - ndc].

A partire da questa data, la questione della determinazione sperimentale della grandezza c₀= è stata definitivamente accantonata [APPENDICE A2].

Ora, oltre a quelle "di natura filosofica", è opportuno tenere in conto le seguenti considerazioni:

a) Tutti i risultati sperimentalmente provati attribuiti alla teoria della relatività ristretta (contrazione dei corpi in movimento, dilatazione temporale, variazione della massa inerziale con la velocità, effetto Doppler trasversale) possono essere coerentemente interpretati sulla base dell'ipotesi c₀ ≠ c_M e conseguentemente non possono essere considerati come prove indirette della validità della teoria einsteiniana.

b) I risultati che, nell'interpretazione conseguente all'ipotesi c₀ ≠ c_M differiscono da quelli della teoria della relatività ristretta, non sono mai stati oggetto di verifiche sperimentali tali da decidere quali, tra essi, siano sperimentalmente fondati.

 
È facile verificare, infatti, che nell'ipotesi, gli esperimenti di Michelson e Morley, Kennedy e Thorndike [24] consentono la deduzione delle seguenti relazioni [APPENDICE A3]:

1)

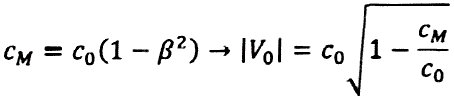                  (12)

dove: β = V₀/c₀; = velocità "assoluta" della Terra.
 

Sostituendo nella (12), ad esempio, i valori; c_M = 299792458 m/s; c₀ = 299800000 m/s (valore scelto in quanto appartiene all'intersezione del valor medio di c₀ e della misura di Rosa e Dorsey) → V₀ = 1500 km/s .

Recenti misure, relative all'anisotropia della radiazione di fondo nella regione delle microonde, hanno indicato una "velocità del gruppo locale" (relativa a questo fondo elettromagnetico): V_LG = (600 ± 50) km/s [25]. Dello stesso ordine di grandezza è la "velocità della Terra" (relativa al fondo astronomico costituito dalle stelle della nostra galassia) misurata da E. Esclangon nel 1926:
V₀= 750 Km/s (incertezza non indicata) [26].

Supponendo che queste velocità relative indichino l'ordine di grandezza di un limite inferiore per la velocità e ponendo nell'equazione (12), ad esempio, il valore: V₀ = 600 Km/s, si ottiene: c₀ = 299793650 m/s.

Conseguentemente l'incertezza di una nuova serie di determinazioni sperimentali della grandezza c₀ tale da consentire di discriminare tra le due ipotesi: c₀ ≠ c_M; c₀ = c_M deve essere almeno inferiore a 600, cioè dell'ordine di 1·10^-6.
 

2)

         (13)

ove: V₀, τ volume e tempo di un orologio stazionario; V, t volume e tempo dello

stesso orologio in moto con velocità assoluta ; K = coefficiente di contrazione

 volumetrica; k_L = k_T; = k coefficiente di contrazione lineare (longitudinale

o trasversale); α = coefficiente di dilatazione temporale.

L'ipotesi c₀ ≠ c_M implica dunque l'isotropia delle contrazioni dei corpi in movimento e delle dilatazioni temporali; di conseguenza, a differenza dei risultati della teoria, einsteiniana, l'esistenza di contrazioni trasversali; e l'assenza o l'esistenza di contrazioni trasversali non è mai stata oggetto di verifica sperimentale.

L'esperimento suggerito, a questo scopo, da Bramanti [27], avviato nel 1979 presso il laboratorio LAFAM del CNR di Pisa, è stato sospeso per mancanza di fondi. Tenendo conto delle relazioni (12) e (13) si ottiene [APPENDICE A4]

                                                                                                             (14)

[T] → t = ατ ↔ τ = kt

L'esperienza mostra, inoltre, quanto segue:
 

1) il rapporto q/m tra la carica elettrica q e la massa inerziale m di una particella carica elettricamente varia con la velocità della particella [28]. 

2) L'equazione di Maxwell-Poynting: P = E/c₀ , che equivale, nell'ottica newtoniana, all'equazione: E = mc₀² fornisce una relazione tra massa inerziale ed energia (elettromagnetica):

      (15) [29].
 

Dalla (14) si ha finalmente:
 

               (16)

                                             (17)

Adottando conseguentemente l'ipotesi: q = cost.; m = m(V) = γm₀ (m₀ = massa a riposo nello spazio di fondo); unitamente al [corrispondente - ndc] principio di conservazione dell'impulso e dell'energia [corrispondente in quanto il "principio di conservazione dell'energia o della materia", così come è insegnato nelle scuole di Stato è sbagliato, o perlomeno ambiguo: una forma di energia non può trasformarsi mai in un'altra solo perché ciò che si trasforma non è che misura aritmetica. Ciò fu descritto in modo esatto già da Julius Robert Mayer (1814-1878), medico e fisico tedesco. Oggi nelle scuole di Stato si studia la cosiddetta legge della conservazione della forza o energia, che poi è detta della conservazione della materia. Ma presentando in questa forma la legge di Mayer la si fraintende radicalmente; infatti Mayer voleva chiarire solo la METAMORFOSI delle energie, NON esprimere il contrario, cioè la conservazione della materia; cfr. "Risposte di Steiner a domande poste nell'anno 1919" in R. Steiner, "Impulsi scientifico-spirituali per lo sviluppo della Fisica. Primo corso di Scienze Naturali. Luce, Colore, Suono, Massa, Elettricità, Magnetismo", Ed. Antroposofica, Milano 2013, pp. 174-176 - ndc], si ottengono le relazioni:

               (18)                               (19)

               (20)

               (21)

La relazione (16) è una legge "normale" di composizione delle velocità nella quale c₀ assume un ruolo normale di velocità finita.

L'impossibilità, fino ad oggi riscontrata, di superare la velocità della luce accelerando particelle cariche elettromagneticamente per mezzo di campi elettrici e magnetici è semplicemente una diretta conseguenza del carattere finito della velocità delle interazioni elettrica e magnetica. In altri termini, le forze elettriche e magnetiche non possono imprimere alle particelle con le quali interagiscono (particelle cariche elettromagneticamente) velocità superiori alla loro specifica velocità di interazione.

Fino ad oggi velocità superluminali sono state osservate solo a livello astronomico [30]. La relazione (17) è una legge anomala di composizione delle accelerazioni che indica, appunto, che "qualcosa non va" nel "principio di conservazione della massa inerziale". Le relazioni (18), (19), (20) sono verificate con incertezze dell' ordine di 10-3 negli acceleratori di particelle, e dell'ordine di 5·10-4 negli esperimenti relativi alla struttura fine dell'idrogeno [31]. QUOZ

Le relazioni (21) differiscono da quelle di Lorentz-Einstein per l'isotropia delle contrazioni delle dimensioni spaziali e delle dilatazioni temporali, come ho già sottolineato (Lorentz-Einstein):

Infine, l'ipotesi c₀ ≠ c_M fornisce, per l'effetto Doppler trasversale e longitudinale, le seguenti relazioni [APPENDICE A5]
 

                          (22)

ove β₀ = V₀c₀; β₁ = V₁/c₀;  = velocità assoluta della sorgente luminosa in movimento.

                          (23)

ove θ₀ e θ₁ sono gli angoli formati dai vettori e e con il vettore che va dal ricevitore alla sorgente.

Come è noto, la teoria di Larmor-Lorentz per l'effetto Doppler è stata verificata nel 1938 da Ives e Stilwell [32] con un'incertezza dell'ordine di 1,5 · 10^-1. Il loro risultato sperimentale è stato in seguito considerato come una "prova indiretta" della validità della teoria einsteiniana. Nel 1962, l'esperimento è stato ripetuto da Mandelberg e Witten [cfr. nota 31] con un'incertezza dello stesso ordine di quella raggiunta da Ives e Stilwell nella regione delle basse velocità e dell'ordine di 35 · 10^-2 nella regione delle alte velocità.

Quanto sopra esposto giustifica la necessità di effettuare una nuova serie di determinazioni sperimentali della grandezza c₀ = con un'incertezza dell'ordine 1·10^-6 ( = ± 300 m/s).

Queste misure possono essere eseguite con metodi puramente elettrici a bassa frequenza determinando direttamente il prodotto ε₀μ₀ e/o il rapporto μ₀ / ε₀ (quadrato della "resistenza d'onda" dello spazio di fondo) confrontando le reattanze di un condensatore calcolabile e di un induttore calcolabile [APPENDICE A6]. In relazione a questa misura il problema principale è costituito dal fatto che, mentre le misure di capacità raggiungono, con i condensatori calcolabili, incertezze dell'ordine di 10^-8, le misure di induttanza consentono, attualmente, incertezze dell'ordine di 10^-6.
 

Se da un lato, di conseguenza, è indispensabile procedere alla costruzione di un induttore calcolabile, dall'altro un primo tentativo di misura può comunque fornire indicazioni utili, anche se non decisive, nella misura in cui le attuali tecnologie consentono di raggiungere incertezze largamente inferiori (10^-6 contro 10^-3) a quelle raggiunte 80 anni fa.

Indice: Prefazione - Determinazione della conducibilità elettrica dello spazio di fondo - Il paradosso di Olbers e la radiazione di fondo - La velocità della luce - Conclusione.

Conclusione

L'arbitrarietà dell'ipotesi: σ₀ = 0, conseguente al primo postulato della teoria della relatività ristretta, è confermata dall'esperienza sia a livello microcosmico che a livello macrocosmico.

Conseguentemente i redshifts galattici, così come la radiazione di fondo, possono essere interpretati come il risultato dello smorzamento dell'energia della radiazione elettromagnetica nell'ambito di un Universo stazionario, e i dati sperimentali relativi ai redshifts galattici consentono una prima valutazione della grandezza σ₀.

La cosiddetta "legge di Hubble" deve considerarsi erronea, mentre il paradosso di Olbers e il paradosso dell"autointerazione" scompaiono.

______________________________

Bibliografia

[1] L. Essen, "La teoria della relatività ristretta. Una analisi critica", Clarendon Press, Oxford 1971.

[2] A. Sommerfeld, "Lezioni di fisica teorica", Vol. II, Elettrodinamica, Sansoni 1961, pag. 51.

[3] J. C. Maxwell, "Teoria elettromagnetica della luce", in "Trattato di elettricità e magnetismo", Vol. II, Ristampa integrale dell'edizione del 1891, Dover 1954, pag. 431.

[4] A. Einstein, "Sull'elettrodinamica dei corpi in moto", Annali di fisica 17, 1905, pag. 891. (Trad. it. in: "Cinquant'anni di relatività", Ed. Giuntine Sansoni 1955, pag. 479).

[5] I. Newton, Lettera a Bentley, in J. C. Maxwell, "Campo ed etere", Boringhieri 1967 (Relatività), pag. 256.

[6] Vedi appendice 2.

[7] A. Einstein, "Considerazioni fondamentali sul postulato della relatività" in "I fondamenti della teoria della relatività generale", Annali di fisica 4, 49, 1916 (traduzione italiana in: "Cinquant'anni di relatività", pag. 510).

[8] A. Einstein, Citato in R. Resnick, "Introduzione alla relatività ristretta", Ed. Ambrosiana, Milano 1969, pag. 2.

[9] J. Rafelsky, L. P. Fulcher, W. Greiner, Phys. Rev. Letters, vol. 27, n. 14, 4 Ottobre 1971, pag. 958.

[10] H. Backe et al., Phys. Rev. Letters, vol. 40, n. 22, 29 maggio 1978, pag. 1443; C. Kozhuharov et al., Phys. Rev. Letters, vol. 42, n. 6, 5 febbraio 1979, pag. 376.

[11] P. S. De Laplace, "Opere", Tomo IV, Libro X, Capitolo VII, pag. 364, Parigi, Stamperia Reale 1845.

[12] R. Becker, "Teoria dell'elettricità", Sansoni, Firenze 1949, vol. I, Capitolo IV, p. 129.

[13] G. Burbidge, "X Simposio Texano sull'astrofisica relativistica". Annali dell'Accademia delle Scienze di N. Y., vol. 375, 1981, p. 152.   

[14] G. S. Hawkins, "Nature", 12 maggio 1962, pag. 563; Il nuovo Cimento, vol. XXIII n. 6, 16 marzo 1962, pag. 1201.
[15] G. De Vaucouleurs, in "Galassie esterne e oggetti quasi stellari". Simposio I.A.U. 44, D. S. Evans Editore 353-66, D. Reidel Publishing Co. Dordrecht 1972, pag. 355.
[16] J. Maddox, "Nature", vol. 307 n. 5949, 26 febbraio 1984, pag. 313.

[17] Olbers, "Opere", Berlino 1894, pag. 135.

[18] J. Chazy, "La teoria della relatività e la meccanica celeste", Tomo II, pag. 204, Gauthier Villars, Parigi 1930.

[19] Laplace, "Opere" Tomo V, Libro XIII, capitolo IV, Parigi Stamperia Reale 1845, pag. 481; Seeliger, Astronomischen Nachrichten Band 137, 1895, pag. 129. Sitzungsberichte Monaco Band 36, 1896, pago 373.

[20] J. F. Mulligan, Am. J. of Phys., vol. 44, n. 10, ottobre 1976, pag. 960.

[21] H. Abraham, "Le misure della velocità V". Congresso Internazionale di Fisica, Parigi 1900. Rendiconti. vol. II, pag. 247.

[22] E. B. Rosa, N. E. Dorsey, "Bulletin of Bureau of Standards", 1907, 3, pag. 433-605.

[23] N. E. Dorsey, "La misura di c". Rendiconti del Congresso Internazionale di Elettricità, Parigi 1932, Seconda Sezione, Relazione n. 10, pag. 189.

[24] A. A. Michelson, E. W. Morely, Am. J. Sci. 334, 333 (1887); R. J. Kennedy, E. M. Thorndike, Phys. Rev. 42, 400 (1932).

[25] D. J. Fixen et al., Phys. Rev. Letters, vol. 50, n. 8, 24 febbraio 1983, pag. 620.
[26] E. Esclangon, Comptes Rendus 182, 12 aprile 1926, pag. 921.

[27] D. Bramanti, "Nuovo Cimento", vol. 45b, n. l, maggio 1978, pag. 90.
[28] P. Caldirola, "Applicazioni e verifiche sperimentali della teoria della relatività ristretta" in "Cinquant'anni di relatività", pag. 399. 

[29] G. N. Lewis, Phil. Mag. 56, vol. 16, n. 95, novembre 1908, pag. 705.  

[30] N. Henbest, "New Scientist", 25 giugno 1981, pag. 848. M. H. Cohen, S. C. nwin, I.A.U. Symposium N°110 VLBI and compact radio sources, Bologna June 27-July 1, 1983, D. Reidel Publishing Company, pag. 95.
[31] H. I. Mandelberg, L. Witten, J.O.S.A., vol. 52, n. 5, maggio 1962, pag. 529.

[32] H. E. Ives, G. R. Stilwell, J.O.S.A., vol. 38, luglio 1938, n. 7, pag. 215.