APPENDICI

(Fonte: R. Monti, "Scritti di critica alla Teoria della Relatività (1984-1987)" Ed. Andromeda, Roma 2018)
A cura di Nereo Villa

Queste sei Appendici sono il continuo della "Parte Prima: Principi per una fisica moderna di Roberto Monti (1984)". Fra di esse, l'appendice A3 è prefigurazione dell'"Appendice 3" del 1986, accennata da R. Monti nella pagina "Un esperimento di divulgazione scientifica" (da me intitolata "Sull'esperimento di fisica non fisica") e completata nel 1986. Buona lettura.

Nereo Villa, Castell'Arquato, 7 giugno 2018

APPENDICE A1


Per il calcolo di σ0 ho usato i dati relativi a due insiemi di galassie con intersezione non nulla, tratti da: G. De Vaucouleurs, W. L. Peters Ap. J. 248, 395, 1981 Sept. 1 G. De Vaucouleurs et al. Ap. J. 248, 408, 1981 Sept. 1.
 

Di questi due insiemi ho fatto varie partizioni disgiunte.

 
Quattro di queste sono state privilegiate; quelle costituite, rispettivamente, da 51, 89, 88, 69 galassie (297 galassie distinte) con:
 

le distribuzioni dei vari insiemi di galassie considerati, in coordinate supergalattiche, sono mostrate in Fig. 4a, b, c, d, e, f.

 

x = 9,92 ± 1,29 Mpc ↔ 29,68 ≤ μ ≤ 30,25;

x = 13,03 ± 1,769 Mpc ↔ 30,26 ≤ μ ≤ 30,85;

x = 17,00 ± 2,14 Mpc ↔ 30,86 ≤ μ ≤ 31,41;

x = 25,10 ± 3,2 Mpc ↔ 31,70 ≤ μ ≤ 32,26;
(μ = modulo di distanza).
 

Il valore ottenuto è: σ0 = (2,85 ± 0,05) ∙ 10-29 (Ωm)-1.


Il valore adottato: (σ0 ± 3Δ) ≡ (2,85 ± 0,05) ∙ 10-29 (Ωm)-1, si è rivelato consistente con i dati relativi a due insiemi di 11 e 16 galassie tratti da M. Aaronson et al. Ap. J. 239, 12-37, 1980 July 1.

 
x = 43,83 ± 4,03 Mpc ↔ 33,00 ≤ μ ≤ 33,4;
x = 57,79 ± 5,91 Mpc ↔ 33,6 ≤ μ ≤ 34,0; che hanno fornito: σ0(11) = 3,0 ∙ 10-29 (Ωm)-1; σ0(16) = 3,0 ∙ 10-29 (Ωm)-1
 

 

Fig. 4a

Distribuzione delle galassie del primo gruppo. N = 51;

 x = 9,92 Mpc; z = 0,0033 → v(c0z) = 988 Km/s.

v > v →▲ (redshift) v < v → ● (blueshift); v = v → ○

 


Fig. 4b

Distribuzione delle galassie del secondo gruppo. N = 89;

 x = 13,3 Mpc; z = 0,0043 → v(c0z) = 1286 Km/s.

v > v →▲ (redshift) v < v → ● (blueshift); v = v → ○

 

 

Fig. 4c

Distribuzione delle galassie del terzo gruppo. N = 88;

 x = 17,0 Mpc; z = 0,0056 → v(c0z) = 1681 Km/s.

v > v →▲ (redshift) v < v → ● (blueshift); v = v → ○

 

 

Fig. 4d

Distribuzione delle galassie del quarto gruppo. N = 69;

 x = 25,10 Mpc; z = 0,00844 → v(c0z) = 2531 Km/s.

v > v →▲ (redshift) v < v → ● (blueshift); v = v → ○

 

 

Fig. 4e

Distribuzione delle galassie del quinto gruppo. N = 11;

 x = 43,83 Mpc; z = 0,0156 → v(c0z) = 4672 Km/s.

v > v →▲ (redshift) v < v → ● (blueshift); v = v → ○

 

 

Fig. 4f

Distribuzione delle galassie del sesto gruppo. N = 16;

 x = 57,79 Mpc; z = 0,0184 → v(c0z) = 5510 Km/s.

v > v →▲ (redshift) v < v → ● (blueshift); v = v → ○

 

 

APPENDICE A2 [accennata in "Elementi" e in "La cintura di sicurezza (prima puntata)" - ndc]
 

Quando, nel 1900, H. Abraham sottolineò la necessità di effettuare una nuova serie di determinazioni sperimentali della grandezza

 

  [1],

 

la miglior misura esistente era stata realizzata, nel 1897, da M. Hurmuzescu (Ann. de Chim. et de Phys. 7ª serie T. X Aprile 1897, pag. 433): c0= (3,001 ± 0,003) 108 m/s (il valore accettato di cM era, a questa data: cM= 2,998 108 m/s).

 
Lo stesso ordine di grandezza fu ottenuto l'anno seguente (1898) da Fabry e Perol (Ann. de Chim. et de Phys. 7ª serie T. XIII Marzo 1898, pag. 404): c0=2,9999 108 m/s (incertezza non indicata).

 
Nel suo rapporto Abraham sceglie il valore: c0 = 2,9973 108 m/s come risultato dell'esperimento di Fabry e Perot: ma lo ottiene partendo dal valore della forza elettromotrice della pila Latinier Oark espresso in volt internazionali, mentre Fabry e Perot riportano il risultato ottenuto dal valore della forza elettromotrice della stessa pila in volt assoluti. Di conseguenza ho ricalcolato il valor medio di c0 tenendo conto del valore originale (Fabry c Perot).

 
Nel 1907 Rosa e Dorsey pubblicano i risultati di una nuova serie di misure di c0 effettuate presso il neonato National Bureau of Standars [2].


Nel 1929 H. L. Curtis (Bureau of Standards Journal of Research III 1929 pag. 63) pubblicò un addendum di Rosa e Dorsey preparato nel 1916 nel quale, tenendo conto di una nuova serie di misure assolute dell'Ohm internazionale, il valore di c0 ottenuto nel 1907 era rivalutato in: c0 = 2,99790 108 m/s "con un'incertezza stimata - da Rosa e Dorsey - in 1·10-4.
 

Curtis concludeva affermando che: "Non ci si può attendere un miglioramento di questo valore fino a quando non sarà effettuata una misura interamente nuova". Durante il Congresso Internazionale di Elettricità, tenutosi a Parigi nel 1932, E. Dorsey [3] stabili come definitivo il valore: c0 = 2,99789 108 m/s, ma l'ultima cifra (9) non ha chiaramente significato dal momento che l'incertezza era ritenuta "non superiore a 40 km/s e probabilmente inferiore".


Dorsey riteneva che questo valore di c0 a quella data, fosse ancora il più preciso esistente, ed era in attesa dei risultati di un analogo esperimento in corso di realizzazione presso il Physicalisch Technische Reichsanstalt. Di questo esperimento, tuttavia, non resta traccia (V. Kose Abteilung Elektrizitat Physicalisch Techuische Bundesanstalt, Comunicazione privata).


Correggendo lo scorretto comportamento scientifico di Abraham, dei 7 risultati scelti nella sua rassegna, 5 (non 4) mostrano la discrepanza tra c0 e cM , e i due rimanenti (Abraham e Thompson) sono chiaramente sbagliati.


Si noti che questa discrepanza era conosciuta, ed è stata rilevata, da almeno due fisici: 1) Dorsey, il quale concluse che "ad ogni modo, l'identità c0 = cM poteva essere accettata sulla base di considerazioni filosofiche"; 2) Sommerfeld (Lezioni di fisica teorica Vol. III Elettrodinamica Sansoni 1961 pag. 51) il quale ricorda anche la misura di Weber e Kohlrausch (1856) che aprì la strada a Maxwell [4], ma conclude affermando che "queste differenze ... nella teoria generale non giocano alcun ufficio".

 

Tra il 1935 e il 1940 conseguentemente all'adozione in via definitiva, da parte delle competenti Commissioni Internazionali, del Sistema di Unità Giorgi (dal quale è stato successivamente derivato il sistema SI) [Sistema Internazionale (delle unità di misura) - ndc] si stabilì di adottare per le grandezze μ ed ε i valori:  μ  = 4π ∙ 10-7 H/m (per convenzione);

Da quest'epoca in avanti la questione della determinazione sperimentale della grandezza c0 = è stata definitivamente accantonata.

 

 

 

APPENDICE A3


L'esperimento di Michelson e Morley consente la deduzione dei coefficienti di contrazione dei corpi in movimento e di dilatazione temporale se si fa la seguente ipotesi fondamentale: le grandezze μ ed ε (così come altre costanti fondamentali quali, ad esempio, la costante gravitazionale G) sono invarianti (risultano avere, cioè, lo stesso valore in ogni sistema di riferimento in moto, relativamente al sistema di riferimento primario); mentre la grandezza cinematica cM = 2L/Δt = λ ∙ ν = ω / k è funzione della velocità assoluta del sistema di riferimento nel quale viene misurata.

 
Dobbiamo anche ricordare che la vera "costante della teoria di Maxwell" è la grandezza c0 (non cM) e che le equazioni di Maxwell valgono "esattamente" nei sistemi di riferimento a riposo relativamente ai sistema di riferimento primario (spazio di fondo). In altri termini: c0 = cM se, nella relazione, c0 = cM ∙ (V), V = 0 → λ0ν0 = c0 , e possiamo indicare questa cM con cM0 [cfr. nota 4].
 

Consideriamo ora il seguente dispositivo:

 

Figura 5 (a destra): U = spazio di fondo; T = terra; (x, y, z) = sistema di riferimento terrestre; V0 = velocità assoluta della Terra nello spazio di fondo; S0 = sorgente luminosa; S1 , S2 = specchi; θ = angolo compreso tra il regolo L e l'asse x; γ = angolo di incidenza; γ' = angolo di riflessione.

Effettuando, in un laboratorio terrestre, una serie di misure cinematiche della velocità della luce emessa da S0 lungo un percorso di andata e ritorno 2L (intendo per "misura cinematica" la determinazione della velocità come rapporto di una lunghezza e di un tempo); ed un'altra serie di misure elettromagnetiche, si ottiene:

 

θ = 0 : cMx = 2L/Δtx; θ = π/2 : cMy = 2L/Δty; c =

 

L'esperienza mostra che


cMx = cMy = cM; Δtx = Δty = Δt


cM = 2L/Δt (≡ λν) = (299792458 ± 1) m/s

c0 = 299800000 m/s

Supponiamo ora che l'effetto risultante al termine dell'intervallo di tempo occorrente ad una forza per imprimere al nostro laboratorio una velocità consista in una variazione nelle dimensioni fisiche elettromagnetiche dei corpi ora in movimento, e in una variazione temporale degli orologi elettromagnetici in movimento.


(1)

 

 

Nelle ipotesi: Vy = Vz = 0 → Vx = || ≠ 0
 

ky = kz = kT (trasversale); kx = K/k² ≡ kL (longitudinale); Lx = kLL; Ly = Lz = kTL; (si sottintende: V0 < c0; se: V0 ≥ c0 , il segnale non raggiunge mai lo specchio-bersaglio).
 

Si ha:
 

1) θ = 0:Δτx = Δταx + Δτrx + ΔτAE; Δτx = Δταx + Δτrx + ΔτAE ove:  Δταx e Δταx ≡ tempi di andata; Δτrx e Δτrx ≡ tempi di ritorno; ΔτAE e ΔτAE tempi di assorbimento-emissione.

 

(2)

 

 

(3)

 

 

|| = c0 (√1-β²)²                                                                         (4)  

 

 

Sostituendo: || = 299800,0 √ 1 - 299800,0/299792,458 1500 Km/s che rappresenta la velocità assoluta della Terra nello spazio di fondo.

 

Nel caso: 2) θ =  π/2 → Δταy ≠ Δτry;  Δταy ≠ Δτry


                                                                        (5) → kT = kL ≡ k

 

 

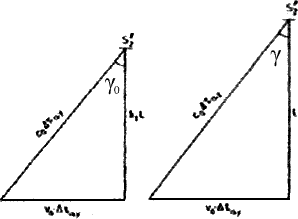
Fig. 6a. Sinistra: angolo di incidenza γ0,

"visto" da un osservatore a riposo in U;

Destra: angolo di incidenza γ, "visto" da

un osservatore a riposo in T.
 

 

Siano infine: (λ0, v0) lunghezza d'onda e frequenza di una sorgente in quiete nel riferimento U ( = 0) → λ0v0 = c0; (λ, v) lunghezza d'onda e frequenza della medesima sorgente in quiete nel riferimento T, mobile rispetto ad U con velocità V0 ≠ 0 (un laboratorio solidale al pianeta) λ0  → CM
 

 

Dalle relazioni (l), (3), (5) →

 

 

 

               (6)




 

 

 

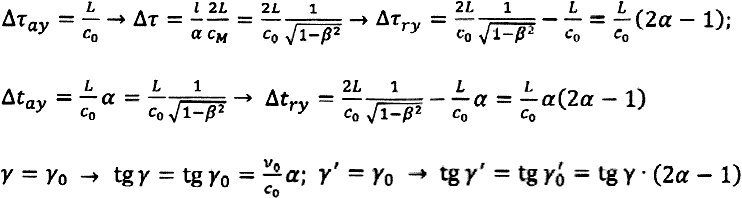
Si noti che l'equazione (5), ove fosse: kT = 1, fornirebbe: α = 1. Risultato paradossale in quanto comporterebbe un'anisotropia assiale, oltre alla ben nota dipendenza lineare (tempo locale), della dilatazione temporale entro un medesimo sistema di riferimento (gli orologi unidimensionali letti lungo l'asse Y dovrebbero segnare un tempo diverso dagli orologi unidimensionali letti lungo l'asse X).
 

Si noti, per concludere, che la relazione: cM = c0 (l - β²) comporta la disequazione: (c0 > cM  per V0 = 0) conformemente ai dati sperimentali (vedi APPENDICE A2).

 

 

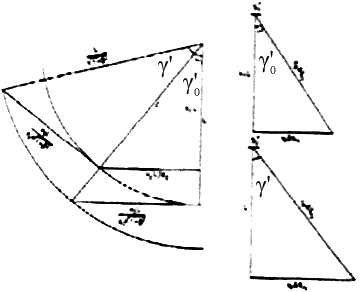
Fig. 6b. A destra, sopra: angolo di riflessione γ'0

"visto" da un osservatore a riposo in U; sotto:

angolo di riflessione γ', "visto" da un osservatore

a riposo in T. A sinistra: costruzione geometrica

dei due triangoli di Fig. 6.

 

 

 

APPENDICE A4

Sia: U (x0 , y0 , z0 , τ) un sistema di riferimento in quiete. T (x, y, z, t) un sistema di riferimento mobile.


 

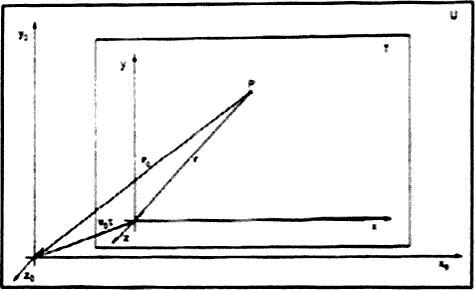
Fig. 7: U = spazio di fondo; T = terra; (x0 , y0 , z0) = sistema di riferimento a riposo in U; (x, y, z) = sistema di riferimento a riposo in T; = velocità assoluta del sistema di riferimento (x, y, z) nel sistema di riferimento (x0 , y0 , z0); τ = tempo proprio del sistema di riferimento (x0 , y0 , z0); = raggio vettore della particella carica P, nel sistema di riferimento (x0 , y0 , z0); = raggio vettore della particella carica P, nel sistema di riferimento (x, y, z).
 

Tenendo conto delle relazioni (1), (6) dell'Appendice A3 si ha:

[L] → = α ( - τ)   ↔   = k (+ τ)

(1)

[T] → t = ατ   ↔   τ = kt

Ora, le relazioni (1) riguardano le dimensioni fisiche (elettro-magnetiche) [L] e [T]. Nulla affermano sulla massa inerziale ([M]) e sulla carica elettrica ([Q]).


L'esperienza mostra tuttavia ciò che segue:


1) il rapporto q/m tra la carica elettrica q e la massa inerziale m di una particella carica varia con la velocità della particella.
2) l'equazione di Maxwell-Poynting: P = E/c0 , che equivale, nell'ottica newtoniana, all'equazione: E = mc²0 , fornisce una relazione tra massa inerziale ed energia (elettromagnetica):

 

                                                       (2).

 

Dalle (1) si ha inoltre:

 

                            (3)

 

                                  (4)

 

Adotteremo, conseguentemente, l'ipotesi (principio di conservazione della carica elettrica) secondo cui, nel rapporto q/m, sia: q = cost.; m = m (v) .

 

In altri termini:

 

q = q0                                 q0 = q
 

m = m(V0) = γm0              m0 = γ-1m
 

= α ( - τ)             = k (+ τ)                                (5)

t = ατ                           τ = kt

 

Supporremo, infine, che in ogni sistema di riferimento in moto con velocità assoluta costante valgano i principi di conservazione della quantità di moto (seconda legge di Newton) e dell'energia.


Consideriamo ora l'effetto di una forza (longitudinale) agente per un tempo dτ su di una particella inizialmente in stato di quiete ( = 0).

 

Si ha:

 

 

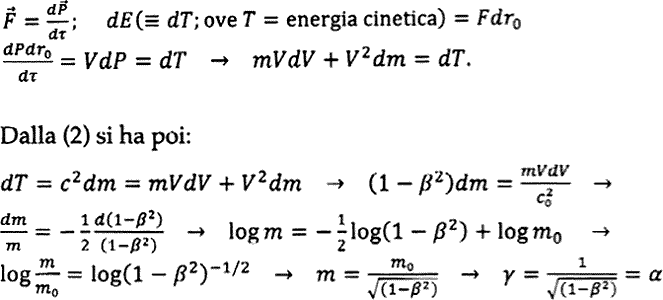
L'insieme completo delle equazioni di trasformazione dimensionali è dunque:
 

[Q] → q = q0                      ↔      q0 = q
[M] → m = αm0                ↔      m0 = km

                                                                                                   (5')
[M] → = α ( - τ)    ↔        = k (+ τ)
[T] → t = ατ                       ↔       τ = kt
 

         (6)

 

                                                          (7)

 

 

Si noti che la relazione P = E/c0 aveva già suggerito a molti autori (Mosengeil, Hasenohrl, Giorgi, ecc.), prima di Einstein, l'idea di un effetto inerziale dell'energia (l"'equivalenza tra massa ed energia": E = mc²0 [5].

 

Le relazioni m = αm0 ; dT = dmc²0 sono tate ottenute, nel modo sopra indicato, da C. N. Lewis nel 1908 [6]. Esse suggerivano "un ritorno alla vecchia (newtoniana) teoria corpuscolare della luce che potrebbe sembrare a molti incompatibile con la teoria elettromagnetica", e sono state di lì a poco "rinnegate" dallo stesso Lewis in un lavoro scritto insieme a Tolman (Lewis e Tolman Phil, Mag. 18, 510, 1909).

 


APPENDICE A5 [citata in "La cintura di sicurezza (prima puntata)" - ndc]
 

Siano: (λ0 , ν0) lunghezza d'onda e frequenza di una sorgente puntiforme S in quiete nel riferimento U; (λ , ν) lunghezza d'onda e frequenza della medesima sorgente in quiete nel riferimento T, mobile con velocità assoluta: = |V0| ; (λ' , ν') lunghezza d'onda e frequenza della medesima sorgente in quiete nel riferimento S, mobile con velocità assoluta: = |V1| ; nel riferimento U; e con velocità relativa: = |V'1| ; nel riferimento T → V1 = (V0 + V'1)  .


Poniamo:

 

 

 


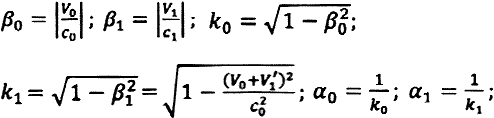
Si ha poi: ν = k0 ν0 ; ν' = k1 ν0 → ν0 = α0ν = α1ν'→ ν' = α0/α1 ∙ ν = k1/k0 ∙ ν

 

 


Si ottiene dunque un effetto Doppler trasversale intrinseco dato dalla relazione:

 

                                                  (1)

 

 

e un effetto Doppler longitudinale dato dalla relazione classica:

 

 

                                                  (2)

 


(la sorgente si muove con velocità assoluta V1; θ0 e θ1 sono gli angoli formati dai vettori e , col vettore che congiunge il ricevitore alla sorgente). Infine (vedi Fig. 8) la (2) si scinde nelle seguenti equazioni:

 

S oss.

 (l'osservatore precede la sorgente) → * ← ■ ; θ0 = θ1 = π

 

 

oss. S

 (l'osservatore segue la sorgente) → ■ → * ; θ0 = θ1 = π

 

 

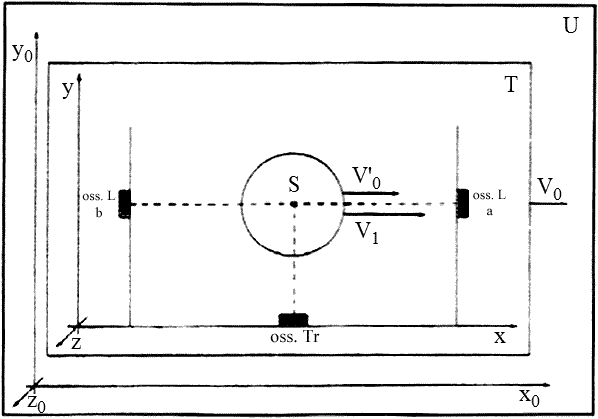
Fig. 8: U = spazio di fondo; T = Terra; (x0 , y0 , z0) = sistema di riferimento a riposo in U;

(x, y, z) = sistema di riferimento a riposo in T; S = sistema di riferimento connesso alla

sorgente luminosa; velocità assoluta della Terra; = velocità assoluta della sorgente

 luminosa; = velocità della sorgente luminosa nel sistema di riferimento (x, y, z);

a, b osservatori longitudinali; Tr = osservatore trasversale.


In lunghezza d'onda si ha poi:


 

 

 

 


APPENDICE A6
La misura della velocità della luce nello spazio di fondo: c0 = può essere eseguita con metodi puramente elettrici in bassa frequenza determinando direttamente il prodotto ε0μ0 e/o il rapporto μ0ε0

(quadrato della resistenza d'onda dello spazio di fondo) mediante il confronto delle reattanze di un campione di capacità calcolabile e di un campione di induttanza calcolabile.

 
Le rispettive capacità C e induttanza L risultano infatti proporzionali a ε0 ed μ0 mediante una lunghezza lC e lL ed un coefficiente numerico kC e kL . Risulta cioè:

 

C = kCε0lC ; L = kLμ0lL                                  (1)

 

Il confronto può non essere eseguibile direttamente dal momento che le reattanze dei due campioni non sono comparabili tra loro alle frequenze metrologicamente più opportune, corrispondenti alle pulsazioni: 10 ÷ 100 Krad/s.

 

Ad esempio, i normali condensatori calcolabili tipo Lampard-Thompson con lunghezze di 0,25 o 0,5 m presentano una capacità C di 0,5 o 1 pF; e quindi, nella gamma: indicata di frequenze, reattanze di 200 ÷ 10 MΩ, mentre l'induttanza L può essere dell'ordine di 100 mH, per cui alle stesse frequenze fornisce una reattanza di 1 ÷ 10 KΩ. La capacità del condensatore calcolabile può comunque essere trasferita a quella C' di un condensatore con valore decadico maggiore più appropriato, scalando, ad esempio con passaggi 10 ÷ 1, attraverso un'opportuna serie di condensatori campioni di valore intermedio.

 

Risulta dunque:

 

C' = nC = nkcε0lC                                  (2)           

 


ove n è un coefficiente numerico determinabile sperimentalmente a livello di 10-7. Un metodo per determinare il prodotto ε0μ0 consiste (metodo a risonanza) nell'alimentare in serie le due reattanze, facendole cioè percorrere dalla stessa corrente, e nell'eguagliare le rispettive cadute di tensione variando ad esempio la frequenza di alimentazione.
 

Alla pulsazione ω0 che consente l'uguaglianza delle tensioni, si ottiene:

 

ω²0LC' = 1

 

ossia la classica relazione di risonanza: ω0L = 1/ω0C'


                                  (3)


Il prodotto si può così dedurre a livello di 10-7, in quanto funzione (oltre dei coefficienti numerici kC e kL del rapporto n, di due lunghezze lC e lL (determinabili con metodi interferometrici a livello di 10-8) e di una frequenza misurabile con incertezza decisamente più spinta.
 

Il rapporto μ0/ε0 , può essere invece misurato con un metodo (metodo a ponte) in cui le due reattanze costituiscono i lati opposti di un ponte di Maxwell-Wien, avente gli altri due lati costituiti da due resistenze R1 e R2.
 

Risulta all'equilibrio:

                                  (4)

 

da cui:

                                  (5)
 

Anche il rapporto μ0/ε0 si può ricavare a livello di 10-7, perché funzione dei medesimi parametri presenti nel prodotto μ0ε0 con la sostituzione, al posto della frequenza, delle due resistenze R1 e R2 il cui valore può oggi essere riferito alla costante h/e² dell'effetto Hall quantizzato a poche unità per 10-8 (L. Bliek et al. PTB Mitteilungen Vol. 93, 1/1983, pag. 21).


In queste considerazioni si sono trascurati per semplicità i parametri parassiti dei campioni a confronto, la cui influenza può infatti essere eliminata o tenuta in conto come contributo di seconda approssimazione.


Il problema principale da risolvere è l'attuazione di un adatto induttore calcolabile. Infatti, mentre la tecnica dei condensatori calcolabili è ormai consolidata (W. K. Clothier Metrologia vol. I, n. 2 1965, pag. 36; T. Igarashi, M. Kanno et al. IEEE Transactions on Instrurnentation and Measurement Vol. IM-21 n. 4, novernber 1972, pag. 361), per ciò che riguarda i campioni di induttanza calcolabile esistono o indagini solo teoriche, allo stato di tentativo (C. H. Page Journal of Research of the N. B. S. Mathematics and mathematical Physics vol. 67, n. l, (January-March 1963), per individuare un dispositivo duale del condensatore di Lampard-Thompson, o modelli del tipo classico a solenoide (P. W. Harrison - C. H. Rayner, Metrologia n. 1 vol. 3, January 1967, pag. 1; H. E. Linckh F. Brasak, Metrologia vol. 4, n. 3, 1968, pag. 94), i quali richiedono una molteplicità di misure dimensionali che allargherebbero l'incertezza delle misure precedenti alle unità per 10-6.

_______________________________________
 

(*) Desidero ringraziare il Prof. E. Arri dell'istituto Elettrotecnico Nazionale Galileo Ferraris (Torino) per le discussioni su questo argomento e per il suggerimento di questi due differenti modi di misura a bassa frequenza della grandezza c0 .

 

[1] H. Abraham, "Le misure della velocità V". Congresso Internazionale di Fisica, Parigi 1900. Rendiconti. vol. II, pag. 247.

[2] E. B. Rosa, N. E. Dorsey, "Bulletin of Bureau of Standards", 1907, 3, pag. 433-605.

[3] N. E. Dorsey, "La misura di c". Rendiconti del Congresso Internazionale di Elettricità, Parigi 1932, Seconda Sezione, Relazione n. 10, pag. 189.

[4] J. C. Maxwell, "Teoria elettromagnetica della luce", in "Trattato di elettricità e magnetismo", Vol. II, Ristampa integrale dell'edizione del 1891, Dover 1954, pag. 431.

[5] P. Caldirola, "Applicazioni e verifiche sperimentali della teoria della relatività ristretta" in "Cinquant'anni di relatività", pag. 399.

[6] G. N. Lewis, Phil. Mag. 56, vol. 16, n. 95, novembre 1908, pag. 705.