Roberto Monti

Appendice 3

Fonte: R. Monti "Scritti di critica alla Teoria della

Relatività (1984-1987)" Ed. Andromeda, Roma 2018

A cura di Nereo Villa

L'esperimento di Michelson e Morley consente la deduzione dei coefficienti di contrazione dei corpi in movimento e di dilatazione temporale, ove si tenga conto che la vera costante della teoria di  Maxwell è la grandezza c₀, e non c_M, e che le equazioni di Maxwell valgono esattamente nei sistemi di riferimento a riposo relativamente  a uno "spazio di fondo" caratterizzato dalle proprietà ε₀ , μ₀ e σ₀ (a sistemi di riferimento nei quali la radiazione di fondo risulta isotropa) [μ₀ = permeabilità magnetica; ε₀ = permettività elettrica; σ₀ = conduttività elettrica - ndr].

In altri termini, la grandezza cinematica c_M = 2L/Δt = λν = ω/k è funzione della velocità assoluta del sistema di riferimento nel quale viene misurata [a questo punto del libro, pag. 65, il testo non è comprensibile a causa di un errore di stampa, vedi l'immagine sottostante. Presumo che Roberto Monti abbia voluto dire, in altra formula, quanto affermato nell'Appendice A3, e cioè che c_M = c₀ se, nella relazione, c₀ è uguale a c_M ∙ f (V), V = 0 → λ₀ν₀ - ndc]:

 

Errore di stampa nel libro

e possiamo indicare questa c_M con << c_M0 >> [1].

Consideriamo ora il seguente dispositivo:

Fig. 5

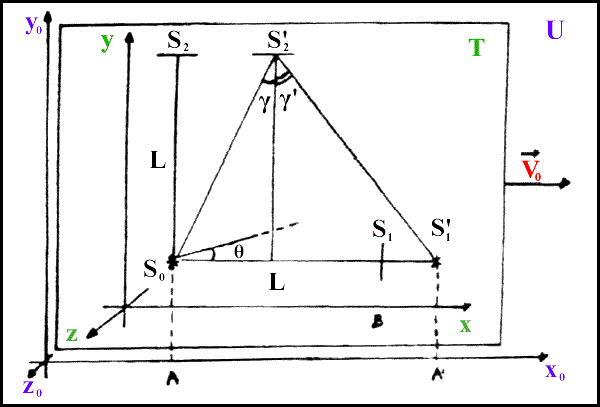
U = spazio di fondo; T = terra; (x, y, z) = sistema di riferimento terrestre; V₀ = velocità assoluta della Terra nello spazio di fondo; S₀ = sorgente luminosa; S₁ , S₂^→ = specchi; θ = angolo compreso tra il regolo L e l'asse x; γ = angolo di incidenza; γ' = angolo di riflessione; (x₀ , y₀ , z₀) sistema di riferimento a riposo in U.

Supponiamo ora che l'effetto risultante al termine dell'intervallo di tempo occorrente ad una forza F per imprimere al nostro laboratorio una velocità V₀ consista in una variazione nelle dimensioni fisiche elettromagnetiche dei corpi ora in movimento, e in una variazione temporale degli orologi elettromagnetici in movimento.

 Siano:

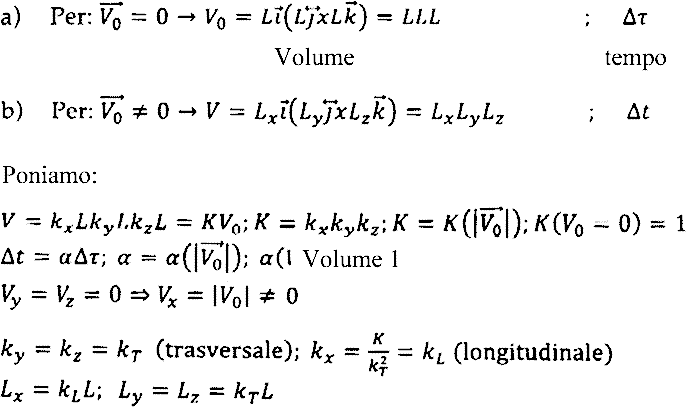
L'esperienza mostra che, misurando il rapporto tra la lunghezza di un percorso di andata e ritorno 2L ed il tempo impiegato dalla luce a percorrerlo (velocità cinematica della luce emessa dalla sorgente S₀) si ottiene:

θ = 0 : c_Mx = 2L/Δt; σ = π/2 : c_My = 2L/Δt_x; c_Mx = c_My = Δt_x = Δt_y =  Δt [2].

c_Mx = 2L/Δt ≡ λν = (299792458 ± 1) m/s [3].

Siano:

c = velocità elettromagnetica della luce misurata nel riferimento T, c = 1/;

V = velocità assoluta del riferimento T misurata nel riferimento T;

c₀ = velocità elettromagnetica della luce misurata nel riferimento U;

V₀ = velocità assoluta di T in U.

V₀Δτ = AA'; VΔt = 1/k AA'; Δt = αΔτ V₀/V = k_Lα = c₀/c V₀/c₀ = V/c = β, invariante                        (2)

1) β = 0 : Δτ_x = Δτ_αx = Δτ_rx = Δτ_AE ; Δτ_x = Δτ_αx = Δτ_rx = Δτ_AE ; ove Δτ_αx , Δτ_αx = tempi di andata; Δτ_rx , Δτ_rx = tempi di ritorno; Δτ_AE , Δτ_AE = tempi di assorbimento-emissione.

Si ha: (c - V) Δt_αx = L; (c - V) Δt_rx = L Δt_αx = L/c = 1/(1- β); Δτ_rx = L/c = 1/(1+ β);

contrariamente all'ipotesi di Einstein

Δt_αx ≠ Δt_rx

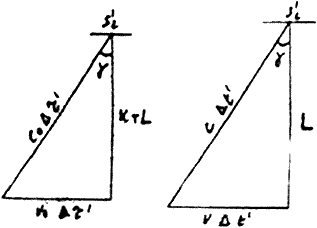
Fig. 6a                  Fig. 6b

Nell'ipotesi:

Δt_x >> Δt_AE Δt_x = Δt = 2L/c_M = 2L/c(1-β²) = c₀/k₁α (1-β²)                (3)

2) θ = π/2: Δτ_αy ≠ Δτ_ry ; Δt_αy ≠ Δt_ry .

Per il cammino ottico di Fig. 6a si ha:        

       (4)

Siano infine: (λ₀, υ₀) lunghezza d'onda e frequenza di una sorgente in quiete nel riferimento U( = 0) → λ₀υ₀ = c₀; (λ, υ) lunghezza d'onda e frequenza della medesima sorgente in quiete nel riferimento T, mobile rispetto ad U con velocità   ≠ 0 (un laboratorio solidale al pianeta) → λ_υ = c_M .

Nell'ipotesi: λ = kλ₀; = ν = 1/α ∙ ν₀                    (5)           

k/α = λ₀ν₀ = c₀/kα (1-β²)              k = √(1-β²) ; K = k³ = (1-β²)^3/2                    (6)        

E nell'ipotesi: c₀ = c √(1-β²) ∙ α = 1 1/√(1-β²)                    (7)  
 

Le relazioni (5), (6), (7) risultano sperimentalmente verificate (effetto Doppler trasversale; vita media del mesone μ...).

 
Tali relazioni comportano, conseguentemente, la validità dell'ipotesi c₀ = c, e delle relazioni:

c_M  = c₀ (1-β²); =            |V₀| = c₀                    (8)          

Sostituendo: 400 = c₀ ∙ √1 - 299792458/c₀           
c₀  = 299793000 m/s che dovrebbe essere il valore "vero" della velocità della luce.

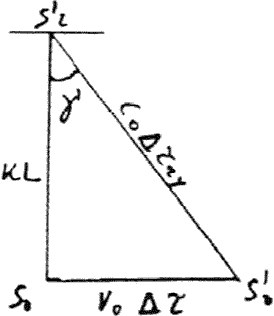
Infine, dalle relazioni: Δτ_αy + Δτ_ry = Δτ

αΔτ = 2L/c_M Δτ = 2L/c₀k

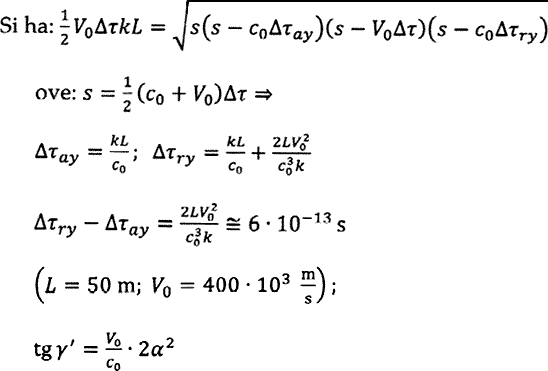
Conseguentemente al fatto che le leggi della riflessione da parte di superfici in movimento sono diverse dalle ordinarie leggi della riflessione (Michelson-Morley 24, p. 342) [24 è il numero della nota di "Elementi" a cui R. Monti fa riferimento, dunque: A. A. Michelson, E. W. Morley, Am. J. Sci. 342 (1887) - ndc].

Si noti che l'anisotropia delle contrazioni dei corpi in movimento comporterebbe una anisotropia assiale, oltre alla ben nota dipendenza lineare (tempo locale), della dilatazione temporale entro un medesimo sistema di riferimento (gli orologi unidimensionali letti lungo l'asse X dovrebbero segnare un tempo diverso dagli orologi unidimensionali letti lungo l'asse Y).
 

Si noti, per concludere, che la relazione: c_M = c₀(1-β²) comporta la disequazione: (c₀ > c_M per V₀ = 0) conformemente ai dati sperimentali (vedi A2).

______________________

[1] J. C. Maxwell, "Teoria elettromagnetica della luce" in "Trattato di elettricità e magnetismo", Vol. II, Ristampa integrale dell'edizione del 1891, Dover 1954.

[2] A. Cacciani, E. Fossat. Comunicazione personale ["Elementi di filosofia naturale. Principi per una fisica moderna. Fondamenti teorici e sperimentali della relatività generale", in R. Monti, "Scritti di critica alla Teoria della Relatività (1984-1987" a cura di Paolo Brunetti, Ed. Andromeda, Roma 2018, p. 184 - ndr].

[3] A. Einstein Erklarung der perhielbewegung des Merkur aus des Aligemeinen Relativitatstheorie Sitzber. Preuss. Akad. D. Wiss. 1915 p. 831; K. Schwarzschild Uber der gravitationsfeld eines massenpunktes nack der Einsteinschen theorie. Sitzber. Preuss. Akad. D. Wiss. 1916 p. 189.