MAPPA della PAGINA: Stato attuale delle GUT... Agg. 09.07.2004
A che punto è il tentativo di unificare meccanica quantistica e relatività generale ?
La ricerca della gravità quantistica è il tentativo di costruire una teoria in cui relatività generale e teoria quantistica dei campi si fondono insieme in modo finalmente valido e coerente. L'obbiettivo, nonostante gli splendidi risultati ottenuti dalle due teorie separatamente, è estremamente complicato e, a tutt'oggi, lontano dall'essere raggiunto. In questo contesto anche una verifica sperimentale, peraltro auspicabile, risulta assai difficoltosa visto che è necessario operare su scale dell'ordine della Scala di Planck, le cui unità sono derivate dalle costanti fondamentali e valgono:
Lunghezza di Planck = 10-35 metri
Tempo di Planck = 10-44 secondi
Massa di Planck = 10-8 kg
Energia di Planck = 1019 GeV
Queste unità diventano rilevanti nel momento in cui le fluttuazioni quantistiche non possono più essere trascurate ma risultano importanti come la forza gravitazionale stessa, momento in cui crolla la struttura di spazio-tempo intesa come un mezzo continuo. Nessun esperimento è però ancora in grado di lavorare in questo ambiente. I tentativi più validi o almeno interessanti degli ultimi anni nell’ambito della ricerca della gravità quantistica sono: Teoria di Kaluza-Klein, Gravità indotta, Teoria perturbativa, Spin Network, Quantizzazione asintotica, Gravità canonica e Teoria delle superstringhe. Mi soffermo brevemente sulle ultime due, attualmente le più in voga. L'approccio Canonico consiste nell'affettare lo spazio-tempo (in termini matematici parliamo di varietà quadridimensionale) in una dimensione temporale e in uno spazio tridimensionale; ognuna di queste fette rappresenta lo spazio in cui ci muoviamo visto a differenti istanti di tempo. L'evoluzione temporale viene ora vista come il passaggio da una fetta all’altra. Le variabili "affettatrici" possono essere scelte con una certa arbitrarietà; una volta in possesso di queste nuove variabili si riscrivono le equazioni di Einstein. Il vantaggio di questa formulazione risiede nel fatto che è possibile riscrivere la relatività generale in una forma matematica simile alle altre forze in natura ( in termini tecnici, la relatività generale assume la forma di una teoria di gauge) e questo, con l'obbiettivo della grande teoria unificata in primo piano, può far sicuramente comodo; inoltre con la nuova formulazione è più facile trovare delle soluzioni alle equazioni della GR. Il programma delle superstringhe consiste nella costruzione di una teoria quantistica della gravitazione completamente differente dalla GR che tuttavia verrebbe ritrovata in questa nuova teoria come limite a bassa energia. La teoria delle superstringhe nasce dal tentativo di far confluire la teoria della supersimmetria nella teoria delle stringhe. Secondo la supersimmetria per ogni bosone esiste il suo gemello fermionico chiamato ad esempio "fotino", "gravitino" etc e per ogni fermione esiste la sua controparte bosonica a spin intero detto ad esempio "squark", "sneutrino" etc . La teoria delle stringhe risale invece al 1968, anno in cui un giovane fisico teorico di nome Gabriele Veneziano scoprì una semplice formula che spiegava il comportamento di alcuni adroni in completo accordo con relatività e meccanica quantistica. L'equazione di Veneziano descriveva appunto una stringa (una corda). Per visualizzare una stringa pensiamo a dei brevissimi fili privi di spessore che vibrano nello spazio; se adesso immaginiamo (per chi ci riesce ! :-) ) di far vibrare queste corde nello spazio-tempo otteniamo delle perturbazioni che identifichiamo con le particelle. L'idea principale della teoria delle superstringhe è riuscire a quantizzare certe entità fondamentali a dieci dimensioni (la superstringa) che si propagano in uno spazio continuo. Noi continuiamo a muoverci in un mondo a 4 dimensioni e le 6 dimensioni in eccesso vengono interpretate come gradi di libertà interni dello spazio-tempo .Attorno a questa teoria c'è moltissimo fermento e il fatto che molti ricercatori si siano buttati nello studio delle superstringhe ne è una conferma fomentata dal fatto che si ritiene che le forze della natura siano unificate in questa struttura, in particolare c'è una certa convinzione che questa teoria possa spiegare in maniera definitiva il problema dell’entropia dei buchi neri e la radiazione Hawking (vedi inciso). Da considerare tuttavia le grandi difficoltà di carattere matematico concettuale di questo tipo di approccio e, come nel caso di altri approcci quale quello canonico prima visto, l'assoluta mancanza di dati sperimentali che permettano di capire quale potrebbe essere la strada migliore da percorrere.
[TOP]
INCISO (sulla radiazione Hawking e teorema di Birkhoff): La radiazione scoperta da Hawking nel 1975 è un effetto puramente quantistico; egli raggiunse questo risultato quantizzando campi di materia sopra una metrica (una soluzione delle equazioni di Einstein) classica. L'origine di questa radiazione è da ricercarsi nella natura non più invariante del vuoto in presenza di un campo gravitazionale. Brutalmente questo significa che uno stato che rappresenta il vuoto per un osservatore, risulta essere pieno di particelle per un altro osservatore ! Intuitivamente possiamo vedere l’effetto Hawking come la cattura da parte del Black Hole, di una particella di una coppia virtuale che si forma in prossimità dell’orizzonte degli eventi. Mentre una particella viene catturata l'altra, ormai priva della sua controparte da annichilare, diventa una particella reale e fugge verso l'infinito dove è rilevata come radiazione termica, alla quale associamo una temperatura ben precisa (e questo è interessante) che rappresenta fisicamente la temperatura del Black Hole. Quindi i Buchi Neri non sono poi tanto Neri :-).
15.09.2003 Il TEOREMA di BIRKHOFF e le sue conseguenze in COSMOLOGIA (sempre per inciso...)
La teoria della Relatività Generale ci insegna che lo spazio non è un semplice contenitore degli oggetti e degli eventi, ma possiede una propria struttura, e questa struttura viene determinata dalla presenza di materia ed energia. Tramite la propria gravità, queste ultime modificano infatti la geometria dello spazio, o, in termini più tecnici, la sua curvatura. Nel 1915 Einstein formulò un insieme di equazioni, che oggi portano il suo nome, che mettono in relazione le proprietà geometriche dello spazio con la quantità di massa-energia presente. Queste equazioni sono estremamente "complicate", ma possono essere risolte in certi casi speciali. L'esempio più semplice è costituito da una configurazione sferica e in quiete di materia (ad esempio una stella o un pianeta). In questo caso, la geometria dello spazio è descritta dalla famosa soluzione di Schwarzschild, che rappresenta lo spazio-tempo attorno ad un buco nero. In generale, lo studio della geometria dello spazio quando la materia che lo influenza non è a riposo diventa molto più complicato. Il teorema di Birkhoff permette di fare un ulteriore passo in avanti: per una configurazione sferica di massa-energia, anche nel caso in cui questa non sia a riposo, la geometria dello spazio circostante è sempre quella di Schwarzschild. In particolare, siccome quest'ultima è una geometria statica, cioè non dipendente dal tempo, lo spazio esterno è a sua volta statico, indipendentemente dallo stato di quiete o meno della materia che lo genera. Si noti che questo risultato riguarda solo la porzione di spazio al di fuori alla materia. Faccio un esempio più concreto: consideriamo una stella sferica, la cui massa distorce lo spazio circostante, e genera una geometria di Schwarzschild. Supponiamo ora che la stella cominci a pulsare (gonfiandosi e sgonfiandosi ritmicamente), ma rimanendo ad ogni istante perfettamente sferica. Il teorema di Birkhoff garantisce che lo spazio esterno non risentirà in alcun modo della pulsazione. Allo stesso modo, quando una stella subisce un collasso (riduce cioè enormemente il proprio volume), fintanto che l'implosione si mantiene sferica, lo spazio circostante rimane immutato. Questo è, per inciso, il motivo per cui le onde gravitazionali sono estremamente deboli: essendo perturbazioni dello spazio che si propagano, e quindi non statiche, non posso essere generate da alcuna configurazione sferica; esse possono sorgere unicamente in presenza delle piccole asimmetrie presenti nelle stelle reali, che sono solo approssimativamente sferiche. Si noti però che se la stella ruota su stessa, il teorema di Birkhoff non è più applicabile. Infatti, in questo caso esiste una direzione privilegiata (quella individuata dall'asse di rotazione), e quindi la simmetria sferica viene rotta. [Un'altra rottura di simmetria :-)] Il teorema di Birkhoff trova le sue più notevoli applicazioni nello studio delle stelle e dei buchi neri. Tuttavia, anche l'Universo nel suo insieme può essere approssimato come una grande sfera di materia, di raggio molto grande (in pratica infinito). Le equazioni che regolano la dinamica dell'Universo (le equazioni di Friedmann, che regolano il suo tasso di espansione o contrazione) possono essere facilmente ricavate proprio tenendo conto di questa approssimazione ed utilizzando il teorema di Birkhoff.
Un pò di cronistoria sulla singolarità
Naturalmente ci sarebbe molto da scrivere sulle singolarità. Cercherò di essere allo stesso tempo esaustivo e il più conciso possibile. Una singolarità è un punto dello spazio-tempo (considerato come una stessa entità geometrica) in cui la forza gravitazionale diviene infinita e quindi la teoria della Relatività Generale di Einstein (che funziona molto bene nel descrivere la struttura dell'Universo) non riesce più a dirci nulla. Questo è stato ricavato per la prima volta partendo da certe soluzioni alle equazioni del campo gravitazionale di Einstein trovate da Karl Schwarzschild nel 1916. Nel punto di singolarità avrò quindi una densità infinita. La singolarità si chiama così perchè difronte ad essa la fisica descritta dalla Relatività si ferma. Nelle soluzioni delle equazioni che descrivono il sistema fisico compaiono degli infiniti (si dice che le soluzioni divergono) e la teoria viene meno. Di conseguenza la dove appaiono degli infiniti la teoria attuale smette di funzionare, e quindi probabilmente deve entrare in gioco una diversa fisica. In realtà si riesce in qualche caso a maneggiare una teoria di campo anche con gli infiniti (per esempio la rinormalizzazione nel modello standard), quindi non è detto che si debba sostituirla radicalmente. Secondo la Relatività Generale le singolarità si formano in due modi. Nel futuro, ad esempio attraverso il collasso gravitazionale delle stelle molto massicce, che avviene inevitabilmente al termine della loro vita dopo aver esaurito tutto il carburante per le reazioni termonucleari. E nel passato, sotto certe ragionevoli condizioni, un universo che si espande deve per forza essere iniziato con una singolarità. Nel 1965 Roger Penrose, che aveva una potente visione geometrica della Relatività, analizzando il comportamento dei coni di luce (che rappresentano in pratica il passato e futuro di un evento nell'universo) dentro forti campi gravitazionali, giunse alla conclusione che se un astro in fase di collasso avesse raggiunto un certo limite chiamato orizzonte degli eventi, allora la singolarità sarebbe stata inevitabile. Egli in pratica dimostrò che la teoria della Relatività Generale prediceva, attraverso certe soluzioni alle equazioni di campo di Einstein, la sua stessa incompletezza, affermando la sicura esistenza delle singolarità. Le singolarità nel futuro, cioè quelle provocate dal collasso gravitazionale di astri massicci, hanno l'interessante proprietà di non essere visibili. Le singolarità infatti si presentano solo in opportune regioni dello spazio-tempo chiamate buchi neri che non ne permettono l'osservazione essendo questi ultimi delimitati da una superificie da cui nessuna particella e informazione può uscire, l'orizzonte degli eventi. Quando un corpo sufficientemente massivo implode, la superficie del materiale collassa sotto il peso dell'attrazione gravitazionale delle sue parti e non importa se questo collasso è perfettamente a simmetrica sferica. La superficie del materiale collassante comincia a vibrare con modi che poi si smorzano a poco a poco e si assestano nello stato sfericamente simmetrico con rilascio di onde gravitazionali. Ogni volta che si forma un buco nero, deve così formarsi al suo interno una singolarità. Si possono scrivere le equazioni che regolano il comportamento della materia fuori del buco nero senza che la singolarità possa influenzare gli andamenti previsti da queste equazioni con la sua presenza. Questa assunzione è detta del censore cosmico in forma debole. Tale congettura protegge la predicibilità delle nostre osservazioni e delle nostre misure fuori dal buco nero ma nulla ci dice su cosa possa accadere dentro, quindi almeno come ipotesi tutto è possibile. Nei buchi neri rotanti (detti di Kerr in onore di Roy Kerr che li definì nel 1963) è possibile teoricamente l'esistenza di cunicoli (wormhole) che potrebbero permettere l'attraversaversamento del buco nero e quindi l'osservazione della singolarità e la riemersione in un altro universo, oppure nel passato del nostro, tanto per fare degli esempi.Se la Relatività non è in grado di dirci nulla sulla singolarità, è chiaro che molte ipotesi esotiche sono possibili quanto indimostrabili: cunicoli tra due universi, cunicoli/scorciatoie tra due due punti dello stesso universo, cunicoli come macchine del tempo, un universo che termina con un Big Cruch (grande collasso finale in un unica singolarità) e simmetricamente nascita di un nuovo universo con una nuova singolarità, il Big Bang. Queste due singolarità di inizio e fine dell'universo in un punto sono dette anche singolarità alle due estremità del tempo. Esiste anche una forma forte della congettura del censore cosmico: essa afferma che queste strutture sono instabili quindi non è possibile attraversare un buco nero o vedere una singolarità. Risultato della congettura del censore cosmico è che la singolarità si trova sempre nel futuro di un eventuale viaggiatore e che quindi rimane sempre inosservabile. Quella nel passato che dovrebbe aver dato origine all'universo con la sua esplosione nel Big Bang, rimane per ovvi motivi ugualmente inosservabile. Quando si applica il principio del censore cosmico in forma forte, tutti i buchi neri di Kerr, Reissner-Nordstrøm et similia (che hanno le interessanti stranezze di tipo worm-hole) risultano tutti vietati perchè in tali buchi neri è falso che la singolarità si trovi nel futuro dell'osservatore. Recentemente si è scoperto che sono ammissibili anche buchi neri con orizzonte degli eventi non sferico, con una topologia arbitraria e con più di una singolarità (per esempio in alcune soluzioni compare una singolarità usuale e una singolarità a stringa detta stringa di Misner che è tagliata in almeno un punto dalla superficie dell'orizzonte degli eventi). Prima di dare una conclusiva e brevissima cronologia dei fatti e scoperte salienti fatte attorno al fenomeno buchi neri-singolarità, vorrei accennare al fatto che si parla di singolarità ogni volta che una determinata formula matematica diverge, cioè tende all'infinito. Se tale formula matematica rappresenta qualche processo, fisico, tecnologico, economico, sociologico, etc. allora si parla di singolarità in quel campo.
Ad esempio recentemente si sta parlando di singolarità tecnologica. La repentina accelerazione del progresso tecnologico porta ad una sempre maggiore velocità nell'elaborazione del processo azione-conseguenza. Il cervello umano può risolvere la maggior parte dei problemi mille volte più velocemente di quanto non possa fare la selezione naturale. Nel creare i mezzi tecnologici in aiuto al cervello per eseguire tali simulazioni ad una velocità molto maggiore, si potrebbe entrare in un regime che è tanto radicalmente diverso dal nostro passato umano quanto noi lo siamo dagli animali inferiori, che invece simulano tale processo alla velocità della selezione naturale. Questo cambiamento può rappresentare una dissipazione di tutte le regole naturali e dell'identità umana in una fuga esponenziale al di là di ogni controllo. Certamente, almeno per i più allarmisti, questa divergenza dello sviluppo tecnologico, non viene considerata meno pericolosa di una singolarità contenuta in un buco nero!
Breve cronologia delle scoperte fatte nel campo dei buchi neri e singolarità.
1783: il pastore anglicano John Michell rettore di Thornhill nello Yorkshire, in un discorso alla Royal Society di Londra dichiara che se esistessero in natura corpi con densità pari a quello del sole e diametro di 500 volte maggiore, la loro luce (intesa allora come corpuscolo materiale e quindi soggetta all'attrazione gravitazionale della Terra) non potrebbe raggiungerci.
1796: il matematico francese Pierre-Simon de Laplace esponeva idee molto simili a quelle di Michell, anche se poi ritrattate in seguito alla scoperta di Young nel 1801 della natura ondulatoria della luce.
1915: Albert Einstein presenta all'accademia Prussiana delle scienze quei straordinari risultati contentuti nella sua Teoria della Relatività Generale, che gli avrebbero garantito fama immortale. Nelle sue equazioni dimostra che la materia e l'energia curvano lo spazio-tempo, e che la curvatura determina la dinamica della materia. Le equazioni del campo gravitazionale contengono sia la geometria dello spazio tempo che le sorgenti del campo stesso.
1916: Karl Schwarzschild, direttore dell'osservatorio di Potsdam, in Polonia, presenta la prima soluzione esatta alle equazioni di Einstein della Relatività Generale. Egli prende in esame una situazione abbastanza semplice, il campo gravitazionale esternamente ad una sfera uniforme di materia non carica ma, nonostante la semplicità, il modello descrive perfettamente cosa accade nelle vicinanze di corpi come il Sole o a grandi distanze, dove il campo gravitazionale è debole e la Relatività si riconduce alle equazioni di Newton. Esiste un punto nelle soluzioni di Schwarzschild in cui l'andamento diverge, cioè ad un valore uguale al raggio detto di Schwarzschild, si presenta un infinito e quindi la soluzione possiede una singolarità.
Negli anni successivi Sir Arthur Eddington dichiara che tale valore limite determina una barriera oltre la quale un astro non può più comprimersi. Chiamò tale limite un "cerchio magico", impenetrabile a qualunque osservazione.
1918: il tedesco H.Reissner e il danese G.Nordstrøm risolvono le equazioni di campo Einstein-Maxwell per sistemi carichi sfericamente simmetrici.
1923: George Birkhoff prova che la geometria dello spazio-tempo di Schwarzschild è l'unica soluzione delle equazioni di campo di Einstein nel vuoto.
1930: l'allora giovanissimo Subrahmanyan Chandrasekhar (che sarà chiamato universalmente "Chandra"), una presenza costante, eclettica e di straordinaria produttività nella fisica del '900, durante il viaggio dall'India a Cambridge che lo porterà ad essere allievo di Eddington, comiciò a fare dei calcoli sulle stelle nane bianche. Trovò che le stelle con massa sopra le 1.4 volte quella del Sole, sarebbero collassata in un oggetto ancora più compatto delle nane bianche.
1931: Lev Davidovic Landau (nome BEN conosciuto da chi ha affrontato il corso di Istituzioni di Fisica Teorica !!) ricavò un risultato analogo a quello di Chandra, ipotizzando l'esistenza delle stelle di neutroni, corpi molto ridotti in dimensioni, che rappresentavano un ulteriore stadio finale per le stelle. Da notare che il primo astro di tale tipo, nella nebulosa del Granchio, sarà osservato solo molti anni dopo, precisamente nel 1968.
formato jpeg ad alta risoluzione [404k]
1934: anche due astronomi di Pasadena, Walter Baade e Fritz Zwicky, conclusero che probabilmente potevano esistere due tipi di stati finali degeneri per le stelle, le nane bianche e le stelle di neutroni.
1933: un serio attacco alla divergenza che si presentava al raggio di Schwarzschild sopraggiunse con il lavoro di un prete belga che divenne presidente della Pontificia Accademia delle Scienze, Georges Lemaitre. Egli ha dimostrato come, con un opportuno cambiamento di coordinate, fosse possibile eliminare il problema. La metrica, con le nuove coordinate, non manifestava più alcun comportamento patologico ma, anzi, funzionava benissimo. Questi scritti attrassero l'attenzione di un cosmologo, Howard Percy Robertson, il quale osservò che il tempo scorre normalmente per un osservatore che decidesse di attraversare l’enigmatico orizzonte degli eventi; questo tempo però apparirebbe man mano sempre più rallentato ad un osservatore che, ben lontano dal buco nero, osservasse il viaggio dell'astronauta. Questi lavori però non ebbero molta fortuna e lo stesso Einstein non perse tempo nel criticarli assieme al concetto di singolarità, affermando che la materia non poteva concentrarsi arbitrariamente.
1939: curiosamente appena due
mesi dopo la sopracitata critica di Einstein, uscì
un lavoro di Robert Oppenheimer e del suo allievo Hartland
Snyder, che è riconoscituo universalmente come il primo vero
e fondamentale passo verso la scoperta dei buchi neri. Studiando con la
fluidodinamica relativistica il collasso di una stella di massa non
molto superiore a quella del Sole,
che abbia esaurito il combustibile per le reazioni termonucleari, essi hanno
predetto la contrazione inarrestabile e continua che avrebbe fatto spostare
la frequenza della luce verso il rosso fino a che l'astro sarebbe diventato
invisibile. L'inarrestabilità del processo
di contrazione avrebbe poi portato alla creazione di una singolarità
temporale infinita, tagliata fuori da possibilità di comunicazione
con il resto dell'universo. Inoltre un altro allievo di Oppenheimer,
George Volkoff contribuì ad usare le conoscenze dell'epoca
sulla fisica atomica e nucleare (siamo
in pieno progetto Manhattan da cui sarebbe uscita la bomba atomica)
per calcolare a che cosa sarebbe dovuta assomigliare una stella di
neutroni.
Dopoguerra e anni '60. Dopo la divisione politica nei due blocchi, si è verificato anche una diverso interesse per i buchi neri. All'Est i lavori di Oppenheimer erano citati regolarmente nei testi accademici di fisica, ad esempio, mentre ad ovest la questione fu apparentemente dimenticata. Negli anni '60 la scuola di Mosca di cosmologia e relatività ha portato a tante interessanti scoperte anche nel campo dei buchi neri. Yakov Zel'dovic affermò che essendo la natura dei buchi neri essenzialmente passiva, la sola speranza di rilevarli era quella di riuscire a localizzarli in base agli effetti gravitazionali sulle stelle o nubi di gas circostanti. Come tesi egli ha posto che l'osservazione del cielo in raggi-X doveva permetterci di osservare le strutture più ricche di energia dell'universo, i gas più caldi, la gravità più forte, e quindi indirettamente anche i buchi neri. Negli Stati Uniti l'interesse rifiorì grazie ad un brillante scienziato, George Wheeler. Lui insieme a, David Finkelstein, Martin Kruskal e George Szekeres osservarono, è bene sottolinearlo tutti quanti separatamente, che con un opportuno cambiamento di coordinate si poteva eliminare la singolarità di Schwarzschild, dimostrando così che si tratta di una singolarità apparente dovuta ad una cattiva scelta di coordinate. I tre ricercatori, quasi quarant'anni dopo Schwarzschild, riuscirono nella mirabile impresa di “abbattere” il cerchio magico eretto da Eddington. Quando Kruskal arrivò a questo risultato, gli sembrò troppo banale per essere pubblicato e fu proprio grazie a Wheeler, che poté essere conosciuto dalla comunità scientifica. In questi anni, grazie alle scoperte astronomiche sulle radiogalassie e quasar sopratutto, si parlava ormai pure di buchi neri supermassivi, cioè di oggetti oscuri con masse di milioni o miliardi di volte la massa del sole e delle dimensioni un sistema solare. Le prove osservative della loro esistenza, oggi sono persino più cogenti di quelli di taglia stellare. Galassie giganti vicine come M 87 (Virgo-A), o galassie attive (i cosidetti nuclei galattici attivi) sono le migliori possibilità di scoprire gli effetti della presenza di questi buchi neri giganti. Con questa impresionate serie di scoperte astrofisiche e con l'affinamento delle tecniche matematiche più potenti fiorirono così gli studi teorici. Si può dire che per la relatività e buchi neri si sono delineate dopo la guerra tre scuole principali: quella di Cambridge fondata da Eddington e proseguita con Dennis Sciama, Chandrasekhar, Roger Penrose e Stephen Hawking, l'altra a Mosca guidata da Zel'dovic e la terza a Princeton guidata da Wheeler che può reputarsi il padre del termine buco nero.
Elliptical Galaxy M87 (NGC 4486), type E1, in Virgo
Right Ascension |
12 : 30.8 (h:m) |
|---|---|
| Declination | +12 : 24 (deg:m) |
| Distance | 60000 (kly) |
| Visual Brightness | 8.6 (mag) |
| Apparent Dimension | 7.0 (arc min) |
1963: il fisico neozelandese Roy Kerr, ha risolto le equazioni di Einstein nel vuoto per campi gravitazionali generati da sistemi massivi rotanti. Queste soluzioni sono piuttosto intriganti poichè come già detto sopra, presentano una struttura tale da poter teoricamente permettere l'esistenza dei wormhole, e quindi di viaggi nel tempo e osservazioni della singolarità.
1964: il matematico Roger Penrose a Cambridge prova che una stella implodente necessariamente deve produrre una singolarità una volta che abbia formato l'orizzonte degli eventi.
1965: Ezra Newman, insieme a E. Couch, K. Chinnapared, A. Exton, A. Prakash, e Robert Torrence risolve le equazioni di Einstein-Maxwell per sistemi massivi rotanti e carichi.
1967: Werner Israel dimostra che tutti i buchi neri non rotanti sono oggetti semplici e la sola proprietà necessaria a caratterizzarli e a differenziarli, è la massa.
1968: Brandon Carter usa la teoria di Hamilton-Jacobi [ben cnosciuti da chi ha fatto meccanica analitica :-)] per derivare equazioni del moto al primo ordine per il moto di particelle cariche immerse nel campo gravitazionale esterno di un buco nero di tipo Kerr-Newman.
1969: Roger Penrose discute il processo (che porterà il suo nome) per l'estrazione dell'energia rotazionale da un buco nero di tipo Kerr. Questa sarà un'intuizione molto importante che dimostra che i buchi neri sono un po' meno neri di quanto si creda e che culminerà pochi anni dopo nei lavori di Hawking. Nondimeno sarà importante per le ricadute sulle osservazioni e teorie astrofisiche dei nuclei galattici attivi, sulla loro energetica e sulla effettiva osservabilità dei buchi neri grazie alla loro attività. Nello stesso cruciale anno Penrose enuncia inoltre i suoi famosi teoremi sulla congettura del censore cosmico, e sulla conseguente invisibilità delle singolarità.
1971: le osservazioni che da anni erano state fatte con i satelliti nei raggi-X della sorgente Cygnus X-1, portano tale sorgente ad essere considersata il primo esempio di probabile candidato per un sistema stellare binario in cui una delle due compagne è un buco nero. Edwin Salpeter afferma in proposoto che un buco nero in Cygnus X-1 è l'ipotesi più prudente.
1972: a Cambridge un allievo di Penrose, Stephen Hawking in collaborazionme con George Ellis fa entusiasmanti scoperte nel campo dei buchi neri. Egli prova che l'orizzonte degli eventi classico non può decrescere. Nello stesso anno Hawking enuncia insieme a James Bardeen e Brandon Carter, quattro leggi per la dinamica dei buchi neri in analogia alle leggi della termodinamica e due principi analoghi al primo e secondo principio della termodinamica. Sempre in quell'anno Jacob Bekenstein suggerisce che un buco nero abbia una entropia proporzionale alla superficie dell'orizzonte degli eventi dovuta ad effetti di perdita di informazione e conseguente aumento di disordine sotto l'orizzonte.
1973: David Robinson, partendo dal lavoro di Carter del '68 e quelli di Hawking, dimostra la congettura di Wheeler, oggi conosciuta come Teorema No Hair. Lo stadio finale di una stella collassante è ristretto a sole sole quattro possibilità e queste sono le quattro soluzioni delle equazione di Einstein per buchi neri rotanti (di Kerr), e fatto fondamentale, i parametri che intervengono in queste soluzioni sono solo la massa la velocità di rotazione e la carica.
1974: Stephen Hawking applicando la teoria quantistica dei campi ai buchi neri dello spazio-tempo, mostra che essi irradiano particelle con uno spettro di corpo nero, e che questo processo può portarli all'evaporazione. E' la più importante delle sue scoperte e che gli ha valso la laurea honoris causa a Cambridge, nonchè la cattedra di fisica che un tempo era stata di Sir Isaac Newton.
1975: le notevoli scoperte sui buchi neri dei primi anni '70 portarono di nuovo Chandrasekhar a riversare la sua energia intellettuale su questi oggetti. Ne è scaturito, anni dopo, un trattato sulla matematica dei buchi neri pieno di virtuosismi matematici ed elaborate manipolazioni teoriche, autodisciplinate dalla sua consueta precisione e che uscì in stampa quando lui aveva 72 anni. Il recente satellite spaziale americano per osservazioni del profondo cielo nei raggi-X e dedicato principalmente a cercare prove stringenti dell'esistenza dei buchi neri è stato chiamato Chandra in suo onore.
Mi sembra bello far terminare quindi questa cronistoria, che è partita da Michell, con il telescopio spaziale Chandra.
12.09.2003
Un plasma turbolento
Le osservazioni sono state fatte usando il telescopio 10-m Keck II delle Hawaii. Un team di astronomi dell’Università della California di Los Angeles (UCLA) ha annunciato di aver osservato condizioni piuttosto turbolenti nel plasma caldo che viene risucchiato dal gigantesco buco nero situato al centro della nostra galassia, la Via Lattea, a circa 26.000 anni luce di distanza dalla Terra. Si tratta della prima rivelazione di plasma caldo alle lunghezze d’onda infrarosse, dove è emessa la maggior parte dell’energia disturbata del plasma, ed è stata effettuata grazie al telescopio Keck II da 10 metri delle isole Hawaii. Il plasma è uno stato di materia calda e ionizzata, differente dai solidi, dai liquidi e dai gas, che si ritiene costituire più del 99 per cento dell'universo visibile. Le precedenti osservazioni alle lunghezze d'onda radio e dei raggi X, indicavano che il buco nero sta assorbendo un flusso di plasma tranquillo, soggetto ad anomalie soltanto il due per cento del tempo. Le osservazioni nell’infrarosso mostrano invece per la prima volta che il flusso di materia di cui il buco nero si nutre assomiglia piuttosto a delle grandi rapide, dove si verificano quasi continuamente turbolenze energetiche dovute a gas in collisione. La ricerca, finanziata dal National Science Foundation (NSF) degli Stati Uniti e disponibile online, sarà pubblicata in futuro sulla rivista "Astrophysical Journal". FINE INCISO.
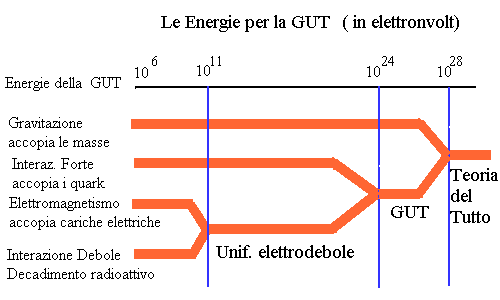
Teorie della Grande Unificazione (Esposizione divulgativa...)
I modelli che prevedono l'unificazione, prendono il nome di Teorie della Grande Unificazione, GUT. Secondo i principi dell'elettrodinamica quantistica, le cariche elettriche interagiscono tramite una particella, chiamata fotone. Analogalmente, anche le forze nucleari debole e forte devono esercitarsi mediante lo scambio di particelle: i bosoni vettori W e Z per la forza debole e i gluoni per quella forte. La GUT si basa sull'esistenza di queste particelle che mediano l'interazione. Nel 1968, tre fisici S. Weinberg, A.Salam e S.Glashow crearono una teoria che comprendeva l'interazione elettromagnetica e quella debole. Dimostrarono che a temperature o energie sufficientemente elevate le due sono effettivamente un'unica interazione. Soltanto col diminuire dell'energia i due aspetti si separano. Questa teoria venne chiamata interazione elettrodebole, e i tre fisici ricevettero il premio Nobel nel 1979. L'interazione è trasportata dai bosoni W che portano sia la carica elettromagnetica che quella debole. Grazie all'interazione elettrodebole si è ottenuta una notevole semplificazione nel mondo delle particelle: ora tutti i fenomeni sono riconducibili all'interazione di leptoni e di quark. Si è altresì notato che teoricamente le due forze, elettrodebole e forte, devono avere lo stesso comportamento ad altissime energie: cioè sono un'unica forza che si differenzia man mano che le energie diminuiscono. La GUT si basa sul seguente ragionamento:
"Poiché la costante di accoppiamento forte decresce quanto più sono vicini i quark interagenti, è opportuno chiedersi se esiste un'energia, e quindi una distanza di interazione alla quale la costante di accoppiamento forte diventi uguale a quella dell'interazione elettrodeboli."
L'energia richiesta è 1024 elettronvolt; a queste energie non dovrebbero esistere interazioni forti o elettrodeboli, ma un'unica interazione, governata da una simmetria che coinvolga quark e leptoni, che risulterebbero del tutto equivalenti e quindi indistinguibili.Si parla di simmetria e precisamente di SU(5) che mette in comunicazione le famiglie leptoniche e barioniche, prevedendo quindi la violazione del numero barionico e leptonico. Quindi tutti gli esperimenti volti a confermare la violazione del numero barionico e leptonico, confermano la teoria della simmetria SU(5), il che equivale a dire che confermano la GUT.
(26.06.2004) Verso una teoria del TUTTO ?
Simmetrie e distanze...
Abbiamo detto che la comprensione del mondo richiede che si rispettino certi principi. Per ovvie ragioni, l'unificazione di tutte le teorie richiederà il rispetto dei più generali principi esistenti: i principi di simmetria. La relatività generale esprime una profonda simmetria dell'universo: essa ci dice che lo stato di moto di un osservatore può essere scambiato con quello di qualsiasi altro supponendo opportuni campi gravitazionali ossia vi è una simmetria fra accelerazione e gravitazione. Per le altre forze fondamentali valgono altre simmetrie relative all'orientamento, alla traslazione e così via (simmetrie di gauge). Oltre a queste si suppone esista un'ulteriore classe detta supersimmetria. Brevemente, secondo la supersimmetria per ogni particella esisterebbe un'altra particella, detta partner supersimmetrico o superpartner, il cui spin è inferiore di mezza unità. Il partner supersimmetrico dell'elettrone (spin 1/2) è il selettrone (spin 1/2 - 1/2 = 0), mentre quello del fotone (spin 1) è il fotino (spin 1 - 1/2 = 1/2). Secondo la supersimmetria, quindi, fermioni e bosoni non sono due gruppi distinti di entità, ma sarebbero accoppiate da un legame di fondo. Nessun partner supersimmetrico è stato finora osservato ma ci sono buone ragioni per credere (e sperare) che la supersimmetria sia valida. È lecito pensare che non esistano altre simmetrie, quindi tanto la relatività quanto il modello standard si basano su alcune proprietà fondamentali dell'Universo e se quest'ultimo è una entità coerente, riesce difficile credere che i suoi pilastri appartengano ad ambiti teorici distinti e incompatibili. L'unità dell'Universo suggerisce che esista una sola teoria che unifichi questi principi di simmetria. Ma abbiamo parlato di due ragioni. La seconda è sperimentale. È facile accorgersi che due magneti si attraggono sempre di più mano a mano che li si avvicina. Ciò significa che il campo elettromagnetico aumenta di intensità al diminuire della distanza. La stessa cosa vale anche per il campo gravitazionale anche se la variazione è quantitativamente diversa. Per i campi nucleari (debole e forte) vale esattamente il contrario, essi diminuiscono al diminuire della distanza. Ciò suggerisce che l'intensità delle forze varia con la distanza (o con l'energia, che è lo stesso). Il fatto sorprendente è che questa variazione è estremamente calibrata. Se la distanza diventa circa uguale alla lunghezza di Planck (ancora lei !) le intensità delle varie forze diventano quasi uguali fra loro. Nel 1991 Amaldi, de Boer e Fürsternau dimostrarono che se vale la supersimmetria questa uguaglianza è perfetta e coinvolge anche la gravitazione. Quindi a dimensioni comparabili con la lunghezza di Planck, proprio quelle dimensioni che creano l'incompatibilità fra relatività e quanti, tutte le forze fondamentali divengono un'unica forza unificata. Resta da vedere quale teoria può descrivere i comportamenti della natura a simili livelli di dettaglio.
 E
in effetti un buon candidato a questo scopo ce l'abbiamo già, la famosa
(o famigerata)
teoria delle stringhe. La teoria delle stringhe
(o delle corde)
nacque nel 1968 quando al
CERN Gabriele
Veneziano si accorse che i risultati di vari esperimenti sulle
particelle elementari potevano essere interpretati usando una vecchia formula
dovuta a Eulero. Un paio di
anni dopo, nel
1970, Nambu,
Nielsen e Susskind escogitarono
un meccanismo che dava conto dell'utilità di questa formula.
Ipotizzarono infatti che le particelle elementari fossero
costituite da minuscole "stringhe"
ossia spaghi chiusi in vibrazione. Il comportamento
è del tutto analogo a quello di una corda di violino.
Se la pizzicate, la corda comincerà a vibrare con una certa frequenza,
ossia un particolare modo di vibrazione. Al modo in cui la corda vibra corrisponde
una nota. Al modo in cui vibra una stringa corrisponde un'energia (o
una massa, che è lo stesso)
di una certa particella elementare. Quindi le stringhe sembrano
dirci che il mondo non è fatto di "oggetti"
diversi, ma di modi diversi di comportamento di una sola primordiale "sostanza".
In secondo, e più tecnico,
luogo, se le stringhe producono massa, allora producono gravità,
quindi devono avere qualcosa a che fare anche con la gravitazione.
E infatti nel 1974
Schwarz e Scherk
mostrarono che dai modi di vibrazione delle
stringhe era possibile ottenere anche una particella con
spin pari a 2: un gravitone. Per la prima volta
si era trovato un (possibile)
meccanismo comune alla formazione delle particelle elementari del modello
standard e al bosone della gravità. A questo punto,
però, la teoria delle stringhe conobbe un momento
di stasi. La fine degli anni Settanta
fu il periodo d'oro del modello standard, in cui si ottennero
moltissimi dati sperimentali e moltissime conferme. La teoria delle
stringhe si presentava come un meccanismo a monte della gravità
e dei fenomeni quantistici, ma non aveva ancora risolto il drammatico conflitto
fra le due grandi teorie del secolo. Il punto
di svolta si ebbe nel 1984
quando Green
e Schwarz mostrarono
in che modo le stringhe potevano
evitare l'incompatibilità. La ragione di ciò
è, vista a posteriori, un'ovvia conseguenza del modo di pensare tipico
della meccanica
quantistica. La formulazione
classica del principio
di indeterminazione è questa:
non possiamo conoscere con precisione piccola
a piacere parametri come, ad esempio, la velocità e la posizione di
una particella. Questo perché, al fine di conoscere
la posizione, dobbiamo colpire la particella con, almeno, un fotone variando
così la sua velocità (e
viceversa). L'idea
implicita è che oggetti dello stesso ordine di grandezza sono in grado
di influenzarsi reciprocamente e noi sfruttiamo questa influenza per ricavarne
conoscenza. Questo fatto è vero in generale.
Ad esempio per sapere
se un pezzo di ferro è magnetizzato dobbiamo avvicinarvi un altro pezzo
e verificare se viene attratto e quindi influenzato. La meccanica
quantistica ha però posto dei rigidi limiti ai modi in
cui questa operazione può essere compiuta. Il
punto cruciale è che se l'oggetto A
è molto più grande dell'oggetto B, il primo
non sarà influenzato dal secondo, come noi non siamo spinti indietro
dalla collisione con un moscerino. E qui viene
il bello: la lunghezza media di una stringa
è proprio la lunghezza di Planck, quindi la schiuma
quantistica, che si manifesta a lunghezze inferiori, non può influenzare
la stringa stessa. Una stringa tipica, quindi, sarà immune dalle disastrose
fluttuazioni quantistiche che si svolgono sotto di essa, come un elefante
è immune dal riportare ferite dall'impatto con un disgraziato lepidottero.
Attenzione, vi vedo e immagino
le vostre obiezioni: "ma
qui vale il limite posto dal principio di indeterminazione".
Infatti un oggetto piccolo
può influenzare uno grande se le energie in gioco sono abbastanza elevate.
Una pallottola può essere non più grande di un moscone, ma sarebbe
difficile convincere le tante vittime delle varie guerre che non ne sono stati
"influenzati".
Allora si sarebbe tentati di dire:
"va bene,
una stringa è troppo grande per essere influenzata dalla schiuma quantistica,
ma questo la condanna ad un'energia fissa, perché se la si dotasse
di maggiore energia potrebbe interagire con la schiuma esattamente come io
posso accorgermi di un dosso su una superficie di marmo ben levigata premendo
sufficientemente forte".
Ma il trucco è che, contrariamente a quanto ci si può aspettare,
se ad una stringa si fornisce maggiore energia essa diventa ancora più
grande e quindi ancora meno soggetta alle fluttuazioni quantistiche.
Non solo, ciò permette
anche di incorporare i risultati della relatività perché i processi
di interazione non saranno più puntiformi, ma "spalmati"
su una regione spaziotemporale estesa e quindi osservatori in diversi stati
di moto la giudicheranno in modo diverso come è tipico della relatività.
Il più piccolo costituente della natura,
in altri termini, è troppo grande per poter essere disturbato dalle
supposte conseguenze paradossali della relatività
e della meccanica
quantistica, ragion per cui dobbiamo
pensare che queste ultime non esistano. Riprendiamo l'esempio
della lastra di marmo levigata. Nessuno di noi potrebbe accorgersi delle irregolarità
microscopiche e tutti saremmo disposti a giurare che tali irregolarità
non esistono e che la lastra è completamente liscia.
Ma nel caso delle stringhe non
si parla di organi sensoriali imperfetti, bensì del più fine
e sensibile costituente dell'Universo. Se la schiuma quantistica
non è in grado di influenzarlo, allora non esiste nulla che ci permetta
di asserire che tale schiuma esiste, perciò possiamo tranquillamente
concludere che non esiste. Accade qualche volta che la matematica si stanchi
di fare il semplice mozzo nel vascello del pensiero e voglia autopromuoversi
a timoniere. Quando ciò succede, la conseguenza
è quella di scambiare semplici esigenze di rigore per affermazioni
di realtà. In particolare
l'esistenza di particelle o regioni di spaziotempo puntiformi
è stata supposta per ragioni di rigore matematico: tra due numeri reali
se ne trova sempre un altro, quindi data una regione di spazio estesa ve ne
è sempre una più piccola in essa contenuta e così via
all'infinito. Ma avevamo il diritto di fare
una simile supposizione ? La teoria
delle stringhe sembra dire di no e sembra rivelarci un sorprendente
messaggio esistenziale: i nostri grandi problemi, ce li eravamo creati da
noi. Tutto risolto allora ?
Magari; diciamo invece che il peggio per il nostro povero
senso comune deve ancora venire. Infatti
la teoria delle stringhe elimina
le fluttuazioni quantistiche che
portavano a calcolare probabilità infinite, ma può condurre
a probabilità negative, cosa che, dal punto di vista matematico, è
altrettanto grave. Ciò è dovuto al disgraziato
fatto che il nostro modo è quadridimensionale (tre
dimensioni spaziali e una temporale).
A questo punto non sembra ci possa essere scampo:
esiste forse qualcosa di più evidente
e meno attaccabile della dimensionalità del nostro spazio
? Esiste, almeno a sentire il matematico tedesco Theodor
Kaluza (1885-1954).
L'idea di fondo è molto "relativistically
correct". Noi possiamo determinare
le dimensioni dello spazio (e
del tempo) solo se
siamo in grado di fare delle misure. Sappiamo che il nostro spazio è
tridimensionale perché possiamo misurare, indipendentemente, una lunghezza,
una larghezza e una altezza. Le tre dimensioni sono pertanto evidenti. Ma
questa idea lascia intendere che potrebbero esistere dimensioni nascoste altrettanto
reali ma non misurabili, magari perché troppo piccole o per altri inconvenienti.
Pensate ad un filo per stendere la biancheria e immaginate di osservarlo da
lontano. Vi sembra unidimensionale,
perché potete misurare (a
occhio) la sua lunghezza,
ma non vi accorgete del suo spessore. Se vi avvicinate abbastanza potete verificare
che ha un'ulteriore dimensione, arrotolata su se stessa. Kaluza
si chiese semplicemente:
e se anche nel nostro spazio esistessero altre
dimensioni arrotolate su loro stesse e quindi invisibili a livello macroscopico
? La domanda cessò di essere un ozioso cavillo matematico
quando, sviluppando questa idea, Kaluza ottenne un risultato
imprevisto e straordinario. Aggiungendo una
dimensione arrotolata su se stessa in modo da diventare estremamente piccola
e quindi nascosta egli ottenne, oltre alle consuete equazioni
della relatività generale per
uno spazio quadridimensionale,
le equazioni di Maxwell
dell'elettromagnetismo. In uno spazio a cinque dimensioni
gravità
ed elettromagnetismo
potevano essere unificati. La teoria di Kaluza-Klein,
dal nome di Oskar Klein (1894-1977)
che la sviluppò ulteriormente, per poco non fece venire un colpo ad
Einstein quando gli venne presentata nel 1919.
Ad uno sguardo più attento, però,
sembrava che tutta questa roba non potesse avere una concreta applicazione
fisica. Sembrava.
Perché come si è detto, la teoria delle stringhe
ha appunto qualche problemino con delle dimensioni mancanti. Se lo spazio
avesse tre dimensioni spaziali ed una temporale,
le stringhe potrebbero vibrare in tre sole direzioni indipendenti: alto-basso,
destra-sinistra, su-giù. Tutte le altre direzioni sarebbero combinazioni
delle prime tre e questo fatto dà luogo a probabilità
negative. Per risolvere il problema bisogna permettere alle stringhe
di vibrare in altre direzioni. Per uno strano
scherzo del destino, peraltro
provvidamente - e sospettosamente
- presente nella storia della scienza,
la teoria
di Kaluza-Klein sembra fatta proprio
alla bisogna. Adattando questa teoria al mondo fisico ne conseguirebbe
che lo spazio non ha solo le dimensioni che siamo abituati a vedere: a livello
microscopico presenta invece altre dimensioni, arrotolate su loro stesse,
che potremmo percepire solo se fossimo piccoli come la lunghezza di
Planck, ossia come una stringa. Già, altre dimensioni, ma
quante ? Non meno di dieci (sì,
dieci, nove spaziali e una temporale !).
Da un certo punto di vista ci va bene,
perché per far funzionare la gravità solo con la supersimmetria
le dimensioni necessarie sono undici, ma riesce comunque arduo pensare al
nostro mondo come un grande filo per stendere che contiene altre sei dimensioni
arrotolate in una struttura complessa detta spazio di Calabi-Yau
dai nomi dei matematici Eugenio Calabi e Shing-Tung
Yau. Questa è la versione a tutt'oggi più accreditata
della teoria delle stringhe, con supersimmetria
e dimensioni arrotolate in spazi di Calabi-Yau.
Ed è l'unico concreto, per quanto traballante, ponticello verso la
terra promessa della Teoria del Tutto. Non
vi sono ancora conferme sperimentali di questo edificio formale e la sua plausibilità
sta soprattutto nel modo in cui riesce ad armonizzare principi che riteniamo
fondamentali, come le simmetrie. Ma, come si è detto all'inizio, la
comprensione del mondo non può fare a meno di principi.
C'è però un elemento che può farci ritenere di aver già
completato almeno la cornice della Grande Unificazione.
La teoria delle stringhe supera un dissidio così profondo
come quello fra relatività generale e meccanica quantistica senza tuttavia
introdurre un punto di vista radicalmente nuovo. Nella
storia della scienza i conflitti fra grandi teorie discordanti hanno sempre
portato a nuove prospettive che superavano entrambi i contendenti.
La relatività generale nacque dal contrasto fra
elettromagnetismo
e meccanica classica; la teoria
dei quanti da quello fra elettromagnetismo
e termodinamica. Ma la
teoria delle stringhe non introduce
nessuna nuova prospettiva, bensì porta alle conseguenze più
estreme idee già contenute nelle grandi teorie che la precedettero.
Questo non significa che il paradigma "stringhesco"
si limiti ad applicare idee non originali, perché esso di fatto riconsidera
i risultati quantistici e relativistici attraverso angolazioni totalmente
nuove giungendo a volte ad esiti che possono sembrare paradossali e incredibili.
Tutto ciò, comunque, fa della teoria delle stringhe
una teoria ancora fondamentalmente e genuinamente quantistica
e relativistica (anzi,
quantorelativistica) e le idee che introduce,
per quanto controintuitive, sono sempre entro uno stile di pensiero che è
proprio della teoria
dei quanti e della relatività. Sembra
pertanto che non assisteremo ad una vera e propria riduzione della relatività
e della meccanica
quantistica ad una nuova teoria superiore, ma
soltanto alla formulazione di una nuova teoria quantorelativistica più
coerente mediante la quale comprenderemo meglio principi che credevamo di
conoscere già. Ciò
significherebbe che tutto sommato dopo venticinque secoli di fisica qualcosa
su cui contare davvero ce l'abbiamo, che i grandi e finali principi dell'universo
sono quelli stabiliti dalla meccanica
quantistica e dalla
relatività generale e
che non potremo mai superare le prospettive su spazio, tempo e interazione
che esse contengono. Da
questo punto di vista, la prima parte della nostra ricerca sarebbe giunta
alla fine. Ma ne siamo
poi così sicuri ?
E
in effetti un buon candidato a questo scopo ce l'abbiamo già, la famosa
(o famigerata)
teoria delle stringhe. La teoria delle stringhe
(o delle corde)
nacque nel 1968 quando al
CERN Gabriele
Veneziano si accorse che i risultati di vari esperimenti sulle
particelle elementari potevano essere interpretati usando una vecchia formula
dovuta a Eulero. Un paio di
anni dopo, nel
1970, Nambu,
Nielsen e Susskind escogitarono
un meccanismo che dava conto dell'utilità di questa formula.
Ipotizzarono infatti che le particelle elementari fossero
costituite da minuscole "stringhe"
ossia spaghi chiusi in vibrazione. Il comportamento
è del tutto analogo a quello di una corda di violino.
Se la pizzicate, la corda comincerà a vibrare con una certa frequenza,
ossia un particolare modo di vibrazione. Al modo in cui la corda vibra corrisponde
una nota. Al modo in cui vibra una stringa corrisponde un'energia (o
una massa, che è lo stesso)
di una certa particella elementare. Quindi le stringhe sembrano
dirci che il mondo non è fatto di "oggetti"
diversi, ma di modi diversi di comportamento di una sola primordiale "sostanza".
In secondo, e più tecnico,
luogo, se le stringhe producono massa, allora producono gravità,
quindi devono avere qualcosa a che fare anche con la gravitazione.
E infatti nel 1974
Schwarz e Scherk
mostrarono che dai modi di vibrazione delle
stringhe era possibile ottenere anche una particella con
spin pari a 2: un gravitone. Per la prima volta
si era trovato un (possibile)
meccanismo comune alla formazione delle particelle elementari del modello
standard e al bosone della gravità. A questo punto,
però, la teoria delle stringhe conobbe un momento
di stasi. La fine degli anni Settanta
fu il periodo d'oro del modello standard, in cui si ottennero
moltissimi dati sperimentali e moltissime conferme. La teoria delle
stringhe si presentava come un meccanismo a monte della gravità
e dei fenomeni quantistici, ma non aveva ancora risolto il drammatico conflitto
fra le due grandi teorie del secolo. Il punto
di svolta si ebbe nel 1984
quando Green
e Schwarz mostrarono
in che modo le stringhe potevano
evitare l'incompatibilità. La ragione di ciò
è, vista a posteriori, un'ovvia conseguenza del modo di pensare tipico
della meccanica
quantistica. La formulazione
classica del principio
di indeterminazione è questa:
non possiamo conoscere con precisione piccola
a piacere parametri come, ad esempio, la velocità e la posizione di
una particella. Questo perché, al fine di conoscere
la posizione, dobbiamo colpire la particella con, almeno, un fotone variando
così la sua velocità (e
viceversa). L'idea
implicita è che oggetti dello stesso ordine di grandezza sono in grado
di influenzarsi reciprocamente e noi sfruttiamo questa influenza per ricavarne
conoscenza. Questo fatto è vero in generale.
Ad esempio per sapere
se un pezzo di ferro è magnetizzato dobbiamo avvicinarvi un altro pezzo
e verificare se viene attratto e quindi influenzato. La meccanica
quantistica ha però posto dei rigidi limiti ai modi in
cui questa operazione può essere compiuta. Il
punto cruciale è che se l'oggetto A
è molto più grande dell'oggetto B, il primo
non sarà influenzato dal secondo, come noi non siamo spinti indietro
dalla collisione con un moscerino. E qui viene
il bello: la lunghezza media di una stringa
è proprio la lunghezza di Planck, quindi la schiuma
quantistica, che si manifesta a lunghezze inferiori, non può influenzare
la stringa stessa. Una stringa tipica, quindi, sarà immune dalle disastrose
fluttuazioni quantistiche che si svolgono sotto di essa, come un elefante
è immune dal riportare ferite dall'impatto con un disgraziato lepidottero.
Attenzione, vi vedo e immagino
le vostre obiezioni: "ma
qui vale il limite posto dal principio di indeterminazione".
Infatti un oggetto piccolo
può influenzare uno grande se le energie in gioco sono abbastanza elevate.
Una pallottola può essere non più grande di un moscone, ma sarebbe
difficile convincere le tante vittime delle varie guerre che non ne sono stati
"influenzati".
Allora si sarebbe tentati di dire:
"va bene,
una stringa è troppo grande per essere influenzata dalla schiuma quantistica,
ma questo la condanna ad un'energia fissa, perché se la si dotasse
di maggiore energia potrebbe interagire con la schiuma esattamente come io
posso accorgermi di un dosso su una superficie di marmo ben levigata premendo
sufficientemente forte".
Ma il trucco è che, contrariamente a quanto ci si può aspettare,
se ad una stringa si fornisce maggiore energia essa diventa ancora più
grande e quindi ancora meno soggetta alle fluttuazioni quantistiche.
Non solo, ciò permette
anche di incorporare i risultati della relatività perché i processi
di interazione non saranno più puntiformi, ma "spalmati"
su una regione spaziotemporale estesa e quindi osservatori in diversi stati
di moto la giudicheranno in modo diverso come è tipico della relatività.
Il più piccolo costituente della natura,
in altri termini, è troppo grande per poter essere disturbato dalle
supposte conseguenze paradossali della relatività
e della meccanica
quantistica, ragion per cui dobbiamo
pensare che queste ultime non esistano. Riprendiamo l'esempio
della lastra di marmo levigata. Nessuno di noi potrebbe accorgersi delle irregolarità
microscopiche e tutti saremmo disposti a giurare che tali irregolarità
non esistono e che la lastra è completamente liscia.
Ma nel caso delle stringhe non
si parla di organi sensoriali imperfetti, bensì del più fine
e sensibile costituente dell'Universo. Se la schiuma quantistica
non è in grado di influenzarlo, allora non esiste nulla che ci permetta
di asserire che tale schiuma esiste, perciò possiamo tranquillamente
concludere che non esiste. Accade qualche volta che la matematica si stanchi
di fare il semplice mozzo nel vascello del pensiero e voglia autopromuoversi
a timoniere. Quando ciò succede, la conseguenza
è quella di scambiare semplici esigenze di rigore per affermazioni
di realtà. In particolare
l'esistenza di particelle o regioni di spaziotempo puntiformi
è stata supposta per ragioni di rigore matematico: tra due numeri reali
se ne trova sempre un altro, quindi data una regione di spazio estesa ve ne
è sempre una più piccola in essa contenuta e così via
all'infinito. Ma avevamo il diritto di fare
una simile supposizione ? La teoria
delle stringhe sembra dire di no e sembra rivelarci un sorprendente
messaggio esistenziale: i nostri grandi problemi, ce li eravamo creati da
noi. Tutto risolto allora ?
Magari; diciamo invece che il peggio per il nostro povero
senso comune deve ancora venire. Infatti
la teoria delle stringhe elimina
le fluttuazioni quantistiche che
portavano a calcolare probabilità infinite, ma può condurre
a probabilità negative, cosa che, dal punto di vista matematico, è
altrettanto grave. Ciò è dovuto al disgraziato
fatto che il nostro modo è quadridimensionale (tre
dimensioni spaziali e una temporale).
A questo punto non sembra ci possa essere scampo:
esiste forse qualcosa di più evidente
e meno attaccabile della dimensionalità del nostro spazio
? Esiste, almeno a sentire il matematico tedesco Theodor
Kaluza (1885-1954).
L'idea di fondo è molto "relativistically
correct". Noi possiamo determinare
le dimensioni dello spazio (e
del tempo) solo se
siamo in grado di fare delle misure. Sappiamo che il nostro spazio è
tridimensionale perché possiamo misurare, indipendentemente, una lunghezza,
una larghezza e una altezza. Le tre dimensioni sono pertanto evidenti. Ma
questa idea lascia intendere che potrebbero esistere dimensioni nascoste altrettanto
reali ma non misurabili, magari perché troppo piccole o per altri inconvenienti.
Pensate ad un filo per stendere la biancheria e immaginate di osservarlo da
lontano. Vi sembra unidimensionale,
perché potete misurare (a
occhio) la sua lunghezza,
ma non vi accorgete del suo spessore. Se vi avvicinate abbastanza potete verificare
che ha un'ulteriore dimensione, arrotolata su se stessa. Kaluza
si chiese semplicemente:
e se anche nel nostro spazio esistessero altre
dimensioni arrotolate su loro stesse e quindi invisibili a livello macroscopico
? La domanda cessò di essere un ozioso cavillo matematico
quando, sviluppando questa idea, Kaluza ottenne un risultato
imprevisto e straordinario. Aggiungendo una
dimensione arrotolata su se stessa in modo da diventare estremamente piccola
e quindi nascosta egli ottenne, oltre alle consuete equazioni
della relatività generale per
uno spazio quadridimensionale,
le equazioni di Maxwell
dell'elettromagnetismo. In uno spazio a cinque dimensioni
gravità
ed elettromagnetismo
potevano essere unificati. La teoria di Kaluza-Klein,
dal nome di Oskar Klein (1894-1977)
che la sviluppò ulteriormente, per poco non fece venire un colpo ad
Einstein quando gli venne presentata nel 1919.
Ad uno sguardo più attento, però,
sembrava che tutta questa roba non potesse avere una concreta applicazione
fisica. Sembrava.
Perché come si è detto, la teoria delle stringhe
ha appunto qualche problemino con delle dimensioni mancanti. Se lo spazio
avesse tre dimensioni spaziali ed una temporale,
le stringhe potrebbero vibrare in tre sole direzioni indipendenti: alto-basso,
destra-sinistra, su-giù. Tutte le altre direzioni sarebbero combinazioni
delle prime tre e questo fatto dà luogo a probabilità
negative. Per risolvere il problema bisogna permettere alle stringhe
di vibrare in altre direzioni. Per uno strano
scherzo del destino, peraltro
provvidamente - e sospettosamente
- presente nella storia della scienza,
la teoria
di Kaluza-Klein sembra fatta proprio
alla bisogna. Adattando questa teoria al mondo fisico ne conseguirebbe
che lo spazio non ha solo le dimensioni che siamo abituati a vedere: a livello
microscopico presenta invece altre dimensioni, arrotolate su loro stesse,
che potremmo percepire solo se fossimo piccoli come la lunghezza di
Planck, ossia come una stringa. Già, altre dimensioni, ma
quante ? Non meno di dieci (sì,
dieci, nove spaziali e una temporale !).
Da un certo punto di vista ci va bene,
perché per far funzionare la gravità solo con la supersimmetria
le dimensioni necessarie sono undici, ma riesce comunque arduo pensare al
nostro mondo come un grande filo per stendere che contiene altre sei dimensioni
arrotolate in una struttura complessa detta spazio di Calabi-Yau
dai nomi dei matematici Eugenio Calabi e Shing-Tung
Yau. Questa è la versione a tutt'oggi più accreditata
della teoria delle stringhe, con supersimmetria
e dimensioni arrotolate in spazi di Calabi-Yau.
Ed è l'unico concreto, per quanto traballante, ponticello verso la
terra promessa della Teoria del Tutto. Non
vi sono ancora conferme sperimentali di questo edificio formale e la sua plausibilità
sta soprattutto nel modo in cui riesce ad armonizzare principi che riteniamo
fondamentali, come le simmetrie. Ma, come si è detto all'inizio, la
comprensione del mondo non può fare a meno di principi.
C'è però un elemento che può farci ritenere di aver già
completato almeno la cornice della Grande Unificazione.
La teoria delle stringhe supera un dissidio così profondo
come quello fra relatività generale e meccanica quantistica senza tuttavia
introdurre un punto di vista radicalmente nuovo. Nella
storia della scienza i conflitti fra grandi teorie discordanti hanno sempre
portato a nuove prospettive che superavano entrambi i contendenti.
La relatività generale nacque dal contrasto fra
elettromagnetismo
e meccanica classica; la teoria
dei quanti da quello fra elettromagnetismo
e termodinamica. Ma la
teoria delle stringhe non introduce
nessuna nuova prospettiva, bensì porta alle conseguenze più
estreme idee già contenute nelle grandi teorie che la precedettero.
Questo non significa che il paradigma "stringhesco"
si limiti ad applicare idee non originali, perché esso di fatto riconsidera
i risultati quantistici e relativistici attraverso angolazioni totalmente
nuove giungendo a volte ad esiti che possono sembrare paradossali e incredibili.
Tutto ciò, comunque, fa della teoria delle stringhe
una teoria ancora fondamentalmente e genuinamente quantistica
e relativistica (anzi,
quantorelativistica) e le idee che introduce,
per quanto controintuitive, sono sempre entro uno stile di pensiero che è
proprio della teoria
dei quanti e della relatività. Sembra
pertanto che non assisteremo ad una vera e propria riduzione della relatività
e della meccanica
quantistica ad una nuova teoria superiore, ma
soltanto alla formulazione di una nuova teoria quantorelativistica più
coerente mediante la quale comprenderemo meglio principi che credevamo di
conoscere già. Ciò
significherebbe che tutto sommato dopo venticinque secoli di fisica qualcosa
su cui contare davvero ce l'abbiamo, che i grandi e finali principi dell'universo
sono quelli stabiliti dalla meccanica
quantistica e dalla
relatività generale e
che non potremo mai superare le prospettive su spazio, tempo e interazione
che esse contengono. Da
questo punto di vista, la prima parte della nostra ricerca sarebbe giunta
alla fine. Ma ne siamo
poi così sicuri ?
DIGRESSIONE...
Sono le equazioni che descrivono il campo elettromagnetico e costituiscono la base dell'elettromagnetismo; studiano la propagazione e l'interazione di energia elettrica e magnetica in un mezzo (o anche nel vuoto) dove sono presenti conduttori e dielettrici e materiali magnetici:
1) rot H = 1/c αD/α + 4πj
2) rot E = 1/c αB/α
3) div D = 4πp
4) div B = 0
5) D = ε E
6) B = μ H
dove H è l'intensità del campo magnetico, E l'intensità del campo elettrico, j la densità di corrente elettrica nei conduttori, ε la costante dielettrica del mezzo, μ la permeabilità magnetica del mezzo; D l'induzione elettrica, B l'induzione magnetica, p la densità volumica di carica elettrica. La prima equazione rappresenta in forma differenziale il teorema della circuitazione di Ampère; in essa il contributo fondamentale di M. consiste nell'aver considerato non solo la corrente di densità j che fluisce nei conduttori elettrici, ma anche la cosiddetta corrente di spostamento di densità Js = ε αE/α = αD/α che si origina nei dielettrici per effetto dell'applicazione di un campo elettrico, attribuendo a detta corrente lo stesso effetto magnetico dovuto alla corrente di conduzione. La seconda equazione rappresenta in forma differenziale la legge dell'induzione elettromagnetica ed esprime l'effetto elettrico dovuto a una variazione di campo magnetico. La terza e la quarta equazione sono ricavate dall'applicazione del teorema di Gauss [Per una illustrazione più approfondita della legge di Gauss file .PDF] rispettivamente al caso di cariche elettriche e magnetiche; in particolare nella quarta equazione è espressa l'impossibilità di separare masse magnetiche di segno opposto. L'importanza delle equazioni di M. è legata al fatto che da esse derivano le leggi di propagazione delle onde elettromagnetiche, nel campo di validità dell'elettromagnetismo classico. M. derivò da esse la previsione teorica dell'esistenza di dette onde prima che H.R.Hertz ne confermasse sperimentalmente l'esistenza nel 1877. Mediante le equazioni di M. possono essere spiegati i fenomeni di diffrazione luminosa senza ricorrere al principio di Huygens il carattere elettromagnetico delle onde luminose fu appunto dimostrato da M. osservando che la velocità di propagazione delle onde elettromagnetiche nel vuoto (calcolata teoricamente) risultava identica alla velocità della luce. Nel caso particolare di campo magnetico costante le equazioni di M. sintetizzano tutte le leggi della elettrostatica; se invece è costante il campo elettrico, sintetizzano le leggi della magnetostatica.
FINE DIGRESSIONE
Utenti connessi...:
CHANDRAst
