LOOP QUANTUM GRAVITY (02.04.2002)
LOOP QUANTUM GRAVITY (02.04.2002)

MAPPA della PAGINA: LOOP QUANTUM GRAVITY... Agg. 20.07.2004
La teoria della relatività generale è stata davvero la più grande elaborazione della fisica teorica degli ultimi settant'anni ? Come mai non è in grado di spiegare le teorie delle superstringhe ? Esistono altre teorie fisico-matematiche che tendono a una spiegazione unitaria ? La teoria della relatività generale è sicuramente una delle tappe principali della storia della fisica, e in particolare del secolo appena trascorso. In generale, però, ogni teoria scientifica è aperta, fin dal momento stesso della sua formulazione, ad essere sostituita da una più completa. La teoria della relatività spiegava fenomeni che la vecchia teoria della gravità non era in grado di spiegare, e lo faceva con eleganza matematica ed economia di pensiero; per questo si impose. Ma presto fu chiaro che, nonostante in accordo con i dati sperimentali, prima o poi anche la teoria della relatività sarebbe stata soppiantata. Perché ? Nel Novecento ha gradualmente preso forma anche una teoria della dinamica del mondo microscopico. L'idea forte, nata dalle osservazioni sperimentali, era che, a livello fondamentale, tutte le quantità fisiche sono disponibili solo in multipli di una quantità elementare, detta quanto. Decenni di studi consentirono prima di gettare le basi di una spiegazione fisico-matematica di questo fenomeno, attraverso la cosiddetta meccanica quantistica, e poi la graduale applicazione di quest'idea al complesso mondo delle interazioni microscopiche. Queste due teorie, la quantistica e la relativistica, nate per spiegare rispettivamente le interazioni microscopiche e la gravità (che, come l'esperienza quotidiana dice, è rilevante su scale macroscopiche), hanno conosciuto notevoli successi, e la questione di quale sia "la più grande" va affidata al gusto del singolo. Il punto, però, è che, per quanto possa essere comodo concettualmente dimenticare il piccolo quando si guarda al grande e viceversa, noi viviamo in un mondo solo. E purtroppo queste due teorie non vanno poi tanto d'accordo tra di loro: si fondano su principi molto diversi, usano teorie matematiche molto diverse, e quando si tenta di rendere l'una simile all'altra, saltano sempre fuori inconsistenze. Per questo motivo, che noi teorici di oggi cerchiamo una teoria che le metta d'accordo, e che spieghi contemporaneamente i fenomeni macroscopici e quelli microscopici, i fenomeni su grande scala della gravità e quelli su piccola scala delle reazioni nucleari. Non solo non è facile trovare proposte coerenti; è anche molto difficile escogitare esperimenti praticamente realizzabili per decidere quale sia quella corretta. La teoria delle superstringhe è una delle candidate, quella su cui attualmente lavorano più scienziati: l'idea fondamentale è che tutte le particelle, inclusi i quanti di gravità, siano descrivibili da piccolissimi oggetti a forma di corda -stringhe, appunto - che, vibrando in modo diverso, vengono viste alle scale delle nostre osservazioni come le varie particelle. Un'altra teoria è nota come gravità quantistica ad anelli ("loop quantum gravity" -- argomento da me trattatto in modo molto esaustivo in questa WEB-PAGE --); nonostante la somiglianza superficiale di questi anelli con le stringhe (somiglianza che fa speculare ai più arditi relazioni tra le due teorie), i presupposti di base sono molto diversi; per esempio, viene predetta una certa discretizzazione dello spazio-tempo, ancora a scale molto piccole, ovviamente. Esistono anche varie altre idee, anche se le due teorie menzionate sono le vie finora più battute. Vale in ogni caso la pena di ricordare che, per quanto si possa dibattere su pregi e difetti di ogni proposta, la parola finale spetta agli esperimenti. Per un approfondimento a un livello un pò più avanzato riguardo a un confronto tra queste due teorie, si veda per esempio l'intervento (in inglese) di Gary Horowitz in una recente conferenza a Roma: "Quantum Gravity at the Turn of the Millennium", disponibile su gr-qc/0011089. Per una storia della ricerca in gravità quantistica, Carlo Rovelli nella stessa conferenza: "Notes for a brief history of quantum gravity", gr-qc/0006061.
Loop quantum gravity provides a general framework for diffeomorphism invariant quantum field theories, within which there is a complete quantization of Einstein's theory of general relativity. There is both a canonical and path integral formalism. In the canonical formalism the Hilbert space of spatially diffeomorphism invariant states has been constructed in closed form. Regularization procedures have been developed which result in finite, diffeomorphsim invariant or covariant operators which represent certain classical diffeomororphism invariant or covariant functions on the phase space. Among these are the area and volume operators, which turn out to have finite, computable spectra. These spectra have been computed in detail. The Hamiltonian constraint and Hamiltonian in certain fixed gauges are also among the operators that have been constructed using these regularization methods, they are represented by finite, diffeomorphism covariant operators. An infinite dimensional space of solutions to the Hamiltonian constraint has been constructed. Some physical operators (those that commute with all the constraints) have been constructed, using several different methods. These include using path integral methods to construct the projection operator onto physical states, making use of matter fields as physical coordinates or explicit operator constructions. Among those that can be so represented are the area and volume operators, thus their spectra represent genuine physical predictions of the theory. The path integral form of loop quantum gravity has been constructed and its relationship to the canonical theory is understood. In the Euclidean case the path integral provides a projection operator onto the space of solutions of the Hamiltonian constraints. This can be used to construct explicit expressions for the expectation values of physical (commuting with all the constraints) observables. These have been computed explicitly by series and numerical methods in several 1+1 dimensional examples. All these results hold for both the Euclidean and Lorentzian signature cases, as well as for extensions of general relativity such as supergravity, and coupling to all usual forms of matter is understood. There are also results in other dimensions such as 1+1 and 2+1. Many of these results have been obtained through several different methods, and the results of these different methods agree up to operator ordering terms, that are by now well understood. Many of the results were first gotten by adopting regularization procedures for products of operators from QCD, and were later verified by being proved as rigorous theorems in mathematical quantum field theory. This applies both to the geometrical operators such as area and volume and the hamiltonian constraint. There remain open questions about the physical interpretation of the solutions to the hamiltonion constraint, these are the subject of much current work and will be discussed in detail below.
Basic results of loop quantum gravity
1)- Kinematics: canonical picture
Loop quantum gravity is a general framework for the construction and study of diffeomorphism invariant quantum field theories. It is now understood in both a canonical and path integral framework. I start with the former. Given a classical field theory whose configuration space includes a space of connections and whose gauge invariances include the corresponding local gauge invariance and diffeomorphism invariance, loop quantum gravity provides a method which results in the construction of a Hilbert space of spatially diffeomorphism invariant and gauge invariant states. The first step is the construction of a kinematical Hilbert space which is a representation of a complete set of basic operators that is complete in the sense that it coordinatizes the phase space. This is the loop algebra. On this space the spatial diffeomorphisms are represented, without anonalies, by unitary operators. The quotient gives the space of diffeomorphism invariant states, together with its inner product. This procedure may be carried out on any theory in the above class, including general relativity, coupled to arbitrary matter fields, including spinors, gauge fields and antisymmetric gauge fields, in any dimension, as well as various extensions such as supergravity. Loop quantum gravity then provides a method for constructing finite operators which represent either diffeomorphism invariant or covariant operators acting on either the space of diffeomorphism invariant states or the kinematical Hilbert space. This is a form of point splitting regularization, modified so as to be diffeomorphism covariant. The main idea of the method is to extract finite parts which, because they do not depend on the regulator, are also independent of background metrics introduced to define the regularization. When applied to spatially diffeomorphism invariant functions of the phase space it yields finite operators on the space of diffeomoprhism invariant states, when applied to scalar functions it gives operators on the kinematical state space that trasform under the action of the unitary representation of the spatial diffeomorphsim group. The operators we have understood by using this method include the area and volume operators, and these are found to have computable discrete spectra. We can couple the theory to matter and use the matter degrees of freedom to label surfaces and then use these to construct, using the regularization procedures we developed, diffeomorphism invariant operators that measure the areas of the surfaces and the volumes they contain.These can also be promoted to real physical operators, as will be described below, and the result is that the spectra of the area and volume operators are genuine physical predictions of quantum general relativity. There are proposals by Amelino-Camelia and others to check these predictions using astrophysical observations, based on the fact that one can check small scale effects on the propagation of light by observing light that has propagated for cosmological scales. (These are discussed in G.Amelino-Camelia et al. {\it Potential Sensitivity of Gamma-Ray Burster Observations to Wave Dispersion in Vacuo}, astro-ph/9712103, Nature 393 (1998) 763-765). It is not possible of course to take any classical observable and turn it into a finite quantum operator. But the operators that have been understood are sufficeint to give a particular basis -the spin network basis- a complete and precise physical interpretation in terms of quantities that measure three geometry. We can also construct operators that measure the conjugate quantities to all these observables. Among the phase space functions we can construct finite representations of are the hamiltonian constraint and hamiltonian in certain fixed gauges. As in any QFT there are ordering ambiguities in the operators that result from the regularization procedures, and these have been studied and are by now largely understood. We also have the spatially diffeomorphism invariant inner products in all these cases. All this is known for both the euclidean and lorentzian theories. The correct way to do the lorentzian signature theories has been worked out in detail by Thomas Thiemann. At the kinematical level, it is possible, given any spatial metric whose curvature invariants are small in Planck units, to construct a quantum state which approximates it as far as all measurements of geometry are concerned which are averaged over surfaces or regions large in Planck units. Some of these states are eigenstates of three geometry operators (these are known as weaves) while others are coherent states, with uncertainty in both three geometry and extrinsic curvature. Thus, kinematically, the theory has semiclassical states, this is necessary, but not sufficient, for the theory to have a good semiclassical limit dynamically. All of these results have been reproduced by the use of a different method, which is mathematically rigorous and based on the study of diffeomorphism invariant measures on spaces of connections. The two methods agree precisely as to the space of states of the theory and the inner product. In the rigorous approach regularization procedures similar to the ones used initially have been developed, and the results of the two methods agree up to well understood operator ordering terms. The rigorous results show that inner products can be chosen at the kinematical level, before imposing diffeomorphism invariance, so that there are no anomolies in the spatial diffeomorphism constraints. The spatial diffeomorphisms are represented by unitary operators and one can mod out by their action and construct completely explicitly the space of diffeomorphism invariant states with inner product (again in all cases mentioned above.) As our calculations had indicated, sufficient operators can be proved to exist rigorously on the space of diffeomorphism invariant states to give the states of that space a complete physical interpretation. In Thiemann's work one also finds theorems which confirm the existence of the hamiltonian constraint for both euclidean and lorentzian theories, up to well understood operator ordering ambiguities. I believe that it is fair to say that we understand this class of theories kinematically as well as QCD or any other conventional QFT in 3+1 dimensions is understood. Given that we understand the exact quantum Hamiltonian constraint, it is fair to say we have a complete description of a large class of theories, within which there is one (up to certain operator ordering ambiguities that are understood) that also has the property that it follows from carrying out a precise quantiation of the Einstein equations. I will address below two questions in detail: what we know about the solutions of this theory and what the correspondence between the classical and quantum theory should be. First, as you asked, some references:
The canonical form of the loop representation was introduced in C.Rovelli and L.Smolin, Nucl Phys B133, 80 (1990), in complete form, except for the specification of the spin network basis, which we found later.
The paper that introduced the different regularization methods used for the area and volume was LSmolin: in {\it Quantum Gravity and Cosmology}, eds J P\'erez-Mercader {\it et al}, World Scientific, Singapore 1992
The spin network basis and the exact forms of the area and volume operators were presented in, C.Rovelli and L.Smolin {\it Discreteness of area and volume in quantum gravity} Nuclear Physics B 442 (1995) 593. Erratum: Nucl. Phys. B 456 (1995) 734; "Spin networks and quantum gravity" gr-qc/9505006, Physical Review D 52 (1995) 5743-5759.
For detailed computations of the spectrum of the volume operator, see R.Loll, Nucl. Phys. B444 (1995) 619; B460 (1996) 143; R. DePietri and C.Rovelli, {\it Geometry eigenvalues and scalar product from recoupling theory in loop quantum gravity}, gr-qc/9602023, Phys.Rev. D54 (1996) 2664; Simonetta Frittelli, Luis Lehner, Carlo Rovelli, {\it The complete spectrum of the area from recoupling theory in loop quantum gravity } gr-qc/9608043; R.Borissov, Ph.D. thesis, Temple, (1996); A.Ashtekar and J.Lewandowski, gr-qc/9711031
For the semiclassical states sharp in three geometry, see Ashtekar, Rovelli and Smolin, Physical Review Letters 69 (1992) 237-240, for coherent like states see a recent paper by Andsdorff and Gupta.
For the construction of diffeomorphism invariant operators using matter fields to locate surfaces, see L. Smolin, {\it Finite diffeomorphism invariant observables for quantum gravity,} Physical Review D 49 (1994) 4028, gr-qc/9302011. There are other papers that accomplish the same thing with different matter fields by Carlo and Viqar Husain.
For the regularization procedure leading to the precise form of the hamiltonian in a certain gauge see: C.Rovelli and L.Smolin, {\em The physical hamiltonian in nonperturbative quantum gravity}, Phys.Rev.Lett. 72 (1994) 446. This method was used by Thiemann, see below, to also construct the hamiltonian constraint in both the euclidean and lorentzian theory.
For Thiemann's work, which establishes the lorentzian signature canonical theory and many of its properties, see T.Thiemann, Quantum Spin Dynamics I-V, Class.Quant.Grav. 15 (1998) 839-905, 1207-1512. gr-qc/9606092, gr-qc/9606089, gr-qc/9606090, gr-qc/9705020, gr-qc/9705021, gr-qc/9705019, gr-qc/9705018, gr-qc/9705017.
A review of loop quantum gravity is C.Rovelli, gr-qc/9710008, also in the electronic journal Living Reviews
The rigorous reformulation of all these results, plus more, were given in, A.Ashtekar and C.J.Isham, Class and Quant Grav 9 (1992) 1069; AAshtekar, J.Lewandowski, D.Marolf, J.T.Thiemann: "Quantization of diffeomorphism invariant theories of connections with local degrees of freedom", gr-qc/9504018, JMP 36 (1995) 519; A.Ashtekar and J.Lewandowski, "Quantum Geometry I: area operator" gr-qc/9602046; hep-th/9412073, J.Geom.Phys. 17 (1995) 191-230, J.Lewandowski, "Volume and quantization" gr-qc/9602035, J. Lewandowski and T.Thiemann, gr-qc/9901015, Class. Quant. Grav. 16 (1999) 2299; Abhay Ashtekar, Alejandro Corichi, Jose.A.Zapata, {\it Quantum Theory of Geometry III: Non-commutativity of Riemannian Structures}, gr-qc/9806041, Class.Quant.Grav. 15 (1998) 2955-2972; J Baez, Spin networks in gauge theory, Adv.\ Math.\ {\bf 117} (1996), 253-272, gr-qc/941107; Spin networks in nonperturbative quantum gravity, in {\sl The Interface of Knots and Physics}, ed.\ Louis Kauffman, American Mathematical Society, Providence, Rhode Island, 1996, gr-qc/9504036.
2)- Uniqueness and variations on the space of states
It is interesting to ask the extent to which the space of states used in loop quantum gravity is unique. One way to pose the question exactly is to ask whether there are other diffeomorphism invariant measures on spaces of non-abelian connections besides the ones used. There are in fact a class of measures that differ on what class of diffeomorphisms are used: smooth, C1, or choices in between. These are understood and their existence is understood to be related to certain operator ordering ambiguities. Besides these there is a conjecture that this class of measures are unique for d>1. (d=1 is special in that there is another class of measures which are the ones based on projective representations of Kac-Moody algebras which are used in conformal field theory, but these do not extend to higher dimensions.). To my knowledge there is at present neither a proof nor a counterexample for this conjecture. Another possibility is to define the space of states in loop quantum gravity not from measures on a configuration space but as representations of a complete (in the sense that they coordinatize the kinematical phase space) set of observables. The choice of algebra used in loop quantum gravity is the loop, or T algebra. There are theorems by Ashtekar and Isham and others about the representation theory of this algebra, given certain technical assumptions one can show that the spaces of states considered above are unique. One can then construct other spaces of states closely related to the loop representation by deforming the algebra of kinematical observables. One way to do this arises from the possibility of quantum deforming the algebra of products of representations of SU(2) that goes into the definition of the algebra. This appears to be required to make certain solutions to the constraints which exist only for non-zero cosmological constant, normalizable. These spaces of states are well defined in that they provide representations to the algebra of observables of quantum gravity (the T-algebra), suitably deformed. To what extent they arise from measures on spaces of connections is presently an open question. Another basis for the space of diffeomorphism invariant states is given by Gambini, Pullin et al, based on Vissiliev invariants. This space of states arises by requiring a certain condition of "loop differentiability" on the states in the kinematical loop representation, and then solving the spatial diffeomorphism constraints within that restricted class. This provides an alternative formulation of the Hamiltonian and diffeomorphism constraints, in which the former differs from those which arise in other formulations by certain operator ordering terms. The exact relationship to the other state spaces studied is not yet completely clear, it is possibly a certain limit of the space of states constructed from representations of the q-deformed spin networks.
We also understand the effects on the theory of several kinds of boundary conditions. There are results concerning finite, timelike boundary conditions, which were first studied as a laboratory to connect loop quantum gravity with conformal field theory. I found using them that the Bekenstein bound, which is a relationship between the area of a boundary and the dimension of the state space of the boundary theory, is a necessary consequence of the kinematics of loop quantum gravity. One thing this has led to is a detailed understanding of the quantum geometry of black hole horizons. Krasnov, one of our students, now at University of California, Santa Barbara (UCSB), initiated the use of these kinds of boundary conditions, taken on null rather than timelike surfaces, for the study of black hole horizons, now many people work on it including Ashtekar, Baez, Corichi, Beetle, Fairhurst etc. These results nicely complement the results on black holes in string theory, in that they apply to ordinary black holes and not just to the extremal and near extremal varieties. One important goal of work in progress is to extend the loop quantum gravity description to those black holes studied by the methods of string theory. With Yi Ling we understand loop quantum gravity now up to N=2 supergravity, and are just at the point when we can attack this problem in detail. There is also an understanding of asymptotically flat boundary conditions, by Thiemann and Andsorff and Gupta.
The finite, timelike boundary conditions were introduced in L.Smolin, {\it Linking topological quantum field theory and nonperturbative quantum gravity} gr-qc/9505028, J.Math. Phys. 36 (1995) 6417. in the euclidean case and L.Smolin, {\it Holographic formulation of quantum general relativity. }, hep-th/9808191, to appear in Phys. Rev. D, in the lorentzian case. With Yi Ling they are now being extended to N=1,2 supergravity.
The extension to black hole event horizons (i.e. null boundaries) was developed in K.Krasnov, gr-qc/9603025, Phys.Rev. D55 (1997) 3505-3513; gr-qc/9605047, Gen.Rel.Grav. 30 (1998) 53-68; gr-qc/9710006, Class.Quant.Grav. 16 (1999) 563-578; A.Ashtekar, J. Baez, A.Corichi, K.Krasnov, Phys.Rev.Lett. 80 (1998) 904-907, gr-qc/9710007; gr-qc/9902015; J.Lewandowski, gr-qc/9907058; A. Ashtekar and K.Krasnov, gr-qc/9804039, published in "Black Holes, Gravitational Radiation and the Universe", Essays in honor of C.V.Vishveshwara, Ed. B.R.Iyer and B.Bhawal, Kluwer, Netherlands; A. Ashtekar, A.Corichi, K.Krasnov, gr-qc/9905089.
The asymptotically flat boundary conditions are described in T.Thiemann, Class.Quant.Grav. 15 (1998) 1463-1485; Class. Quantum Grav. {\bf 12} (1995) 181-198, gr-qc/9705020, and a recent paper by Andsdorf and Gupta (gr-qc/9909053), (gr-qc/9910084) .
We also understand the role of the cosmological constant in the kinemtical framework, which is to force the spin network states to be constructed from the representation theory of quantum deformed SU(2). All this has been worked out in detail, with Borissov and Major with also contributions from Baez. In the case of time like boundary conditions it leads to a complete understanding of the boundary theory in terms of conformal field theory.
Quantum deformed spin networks for the case of non-zero cosmological case were constructed in S.Major and L.Smolin, {\it Quantum deformation of quantum gravity} gr-qc/9512020, Nucl. Phys. B 473 (1996) 267; R. Borissov, S.Major and L.Smolin, {\it The geometry of quantum spin networks} gr-qc/9512043, Class. and Quant. Grav. 12 (1996) 3183 and in L.Smolin JMP, above.
5)- Path integral formulations of the dynamics in loop quantum gravity
The path integral framework for this large class of theories has been worked out during the last three years. In the Euclidean case it is called spin foam. The basic framework is by now understood, so that we have a framework to do path integral calculations to find, given a form of the action or of the hamiltonian constraint, the amplitude to evolve from any spin network to any spin network. As in QCD, several different forms of the action have been proposed, and are under study. These differ by terms which in some cases correspond to the operator ordering ambiguities of the canonical theory. It turns out that spin foam is closely connected with a well-understood mathematical subject, which is Topological Quantum Field Theory (TQFT). This is because the dynamics of general relativity, supergravity etc. all can be understood as arising from certain deformations of TQFT. In fact, all the successes of the loop approach, and in the classical domain the Ashtekar framework can be traced to this fundamental fact. Spin foam models were first investigated by Michael Reisenberger, in an important pair of papers, he was then joined by Carlo Rovelli. An independent line of work starting with TQFT and ending with spin foam was pursued by a group of mathematicians, led by Louis Crane, and including John Baez, John Barrett and several others. Other people who work on spin foam models are Krasnov, Freidel, Iwazawa and Putzio. Carlo Rovelli and Mike Reisenberger have understood in detail the relationship between the path integral and canonical framework, which they showed works as in conventional QFT. The Lorentzian path integral approach is called causally evolving spin networks. It was invented by Fotini Markopoulou by combining the kinematical structure of loop quantum gravity with the causal histories approach as formulated originally by tHooft and Sorkin and collaborators. This and related topics are studied by Gupta, Borissov, Ambjorn, Anagnastoploous, Waalebrook, Des Johnson Renata Loll in Potsdam. There are detailed numerical and analytic results concerning 1+1 and 2+1 systems which can be seen as simple examples of evolving spin networks, which I will describe below. The relationship between the Euclidean spin foam approach and the Lorentzian causally evolving spin network approach has been worked out by Sammer Gupta, by showing how the Lorentzian approach may also be derived from studying evolution in the canonical framework. Using spin foam methods projection operators have been constructed by Rovelli which project onto the space of physical states. This allows the construction of physical operators. I will comment on this below.
The basic papers in spin foam are: M.Reisenberger, {\it Worldsheet formulations of gauge theories and gravity}, gr-qc/9412035; {\it A lattice worldsheet sum for 4-d Euclidean general relativity} , gr-qc/9711052; M. Reisenberger and C.Rovelli, {\it "Sum over Surfaces'' form of Loop Quantum Gravity}, gr-qc/9612035, Phys.Rev. D56 (1997) 3490-3508; J.Barrett and L.Crane, {\it Relativistic spin networks and quantum gravity}; gr-qc/9709028, J.Math.Phys. 39 (1998) 3296-3302;
The relationship between spin foam and the canonical theory is described in detail in C.Rovelli, {\it The projector on physical states in loop quantum gravity}, gr-qc/9806121, Phys.Rev. D59 (1999) 104015.
A recent review by Baez is {\it An Introduction to Spin Foam Models of Quantum Gravity and BF Theory}, gr-qc/9905087; an older review is Baez, {\it Spin foam models}, gr-qc/9709052.
A selection of recent papers on spin foam is: Laurent Freidel, Kirill Krasnov,{\it so(4) Plebanski Action and Relativistic Spin Foam Model}, gr-qc/9804071, Class.Quant.Grav. 16 (1999) 2187-2196; {\it Spin Foam Models and the Classical Action Principle} hep-th/9807092, Adv.Theor.Math.Phys. 2 (1999) 1183-1247; John C.Baez, R De Pietri, {\it Canonical "Loop" Quantum Gravity and Spin Foam Models}, gr-qc/9903076, To appear in the proceeding of the XXIII SIGRAV conference, Monopoli (ITALY), September 21st-25th, 1998; R. De Pietri, L.Freidel, K.Krasnov, C.Rovelli, {\it Barrett-Crane model from a Boulatov-Ooguri field theory over a homogeneous space}, hep-th/9907154;
The basic papers on causally evolving spin networks are: F.Markopoulou, {\it Dual formulation of spin network evolution} preprint, March 1997, gr-qc/9704013; F.Markopoulou and L.Smolin {\it Quantum geometry with intrinsic local causality} preprint, Dec. 1997, gr-qc/9712067, Phys.Rev. D58 (1998) 084032.
The relation between spin foam and causally evolving spin networks is shown in Sameer Gupta, {\it Causality in Spin Foam Models}, gr-qc/9908018;
Detailed numerical results concerning 1+1 systems which can be thought of as simple models of causally evolving spin networks are found in: J.Ambjorn and R.Loll, {\it Non-perturbative Lorentzian Quantum Gravity, Causality and Topology Change}, Nucl.Phys. B536 (1998) 407-434, hep-th/9805108; J.Ambjorn, J.L.Nielsen, J.Rolf, R.Loll, {\it Euclidean and Lorentzian Quantum Gravity - Lessons from Two Dimensions}, hep-th/9806241, Chaos Solitons Fractals 10 (1999) 177-195; J.Ambjorn, K.Anagnostopoulos and R.Loll, {\it Crossing the c=1 barrier in 2d lorentzian quantum gravity}, hep-lat/9909129; {\it A new perspective on matter coupling in 2d quantum gravity} hep-th/9904012.
Numerical results for 2+1 evolving spin networks are in R.Borissov and S.Gupta, {Propagating spin modes in canonical quantum gravity}, gr-qc/9810024.
Let me now turn to the study of dynamics. This must be prefaced by a remark about what we expect to happen in a quantum theory of gravity at the dynamical level, when the theory has been formulated completely non-perturbatively. The main questions are what should be the role of renormalization and how should we expect the classical theory to emerge from the correct quantum theory. The key point is that we know from the kinematical framework that there cannot be an infinite renormalization of the bare Newton's constant. This is shown in detail by the weave construction we invented with Ashtekar and Rovelli (Physical Review Letters 69 (1992) 237-240). This is the construction, at the kinematical level, of quantum states whose expectation values approximate slowly varying classical spatial metrics. The construction requires that the spin network states be discrete in the sense that there are only a finite number of nodes of the spin network states per unit physical volume, measured according to the classical metric. This means that the physical picture forced on us by the results of loop quantum gravity is one in which quantum geometry at the level of diffeomorphism invariant states is necessarily discrete, the continuum can then only arise as an approximation when scales much larger than the Planck scale are probed. It follows form this that the problem of the classical limit is more closely analogous to a problem of critical phenomena in condensed matter theory than to renormalization in ordinary quantum field theory. There is, for the reasons just mentioned, necessarily a finite fixed scale, analogous to the atomic scale, where the quantum geometry is discrete. The classical limit then involves a limit in which the volume of the universe becomes large in these atomic, or Planck units. A lot is known about how to take such limits in statistical mechanics, and there is also a large literature applying methods from statistical physics to study the classical limit in Euclidean quantum gravity, in the conexts of the theory of random surfaces, Regge calculus and dynamical triangulations. We know from these results that there are two separate questions: 1) is there a large volume limit ? 2) will that limit have the property that the expectation value geometry, averaged over a large scale in Planck units, is smooth, so that it can be appriximated by a smooth classical metric ? We know from all of these studies that it can often be the case that 1) is true but 2) is not. This means that the theory is well defined, but does not have a limit which is classical general relativity. This will be the situation unless there is a very special situation in which the dynamics becomes critical in the large volume limit. Critical means approximately scale invariant. In QFT terms, this means that there are massless particles, so correlation functions behave as powers of separations, not as exponentials. When this fails to be the case all correlations are suppressed by exponentially falling factors, and the result is both that there is no long ranged propagation of information and that the average geometry fails to be smooth. Unfortunately, as presently understood, this is the situation with Regge calculus and dynamical triangulations in d=4. Now let me come back to the results on dynamics from loop qauntum gravity. As mentioned above, the Hamiltonian constraint for general relativity was derived explicitely from three different regularization procedures, for both the Euclidean and Lorentzian theories. (by Rovelli and I (also with results by Borissov), by Gambini, Pullin and collaborators and by Thiemann). The results of the different methods differ by well understood operator ordering terms. There is only a small amount of freedom in the result as the requriments that the operator be local when the regularization is removed, but transform correctly as a density under three diffeomorphisms, are rather stringent. The results are strikingly different depending on whether the cosmological constant is zero or nonzero.
Non-zero cosmological constant
In this case there is a good physical state, discovered by Kodama, which is an exact solution to all the constraints and also has a good semiclassical limit. That limit gives rise to a semiclassical interpretation of the state, which is as the ground state in DeSitter spacetime or AntiDesitter spacetime, depending on the sign. When boundaries are introduced this becomes a finite dimensional space of states, whose number grows as the exponential of the area of the boundary, exactly as stipulated by the Bekenstein bound. This all works in supergravity also, at least up to N=2. Different aspects of these states have been studied by Brugmann, Pullin, Gambini and collaborators, Soo, Borissov, Major, -myself- and others. The study of these states seems to require the quantum deformation of the theory, as mentioned above, in order to make the Kodama state normalizable.
{H.Kodama, Prog.Theor.Phys.80:1024,1988}; B.Bruegmann, R.Gambini and J.Pullin, Phys.Rev. Lett. 68, 431 (1992); Gen. Rel. and Grav. 251 (1993); L.Smolin and C.Soo, {\it The Chern-Simons invariant as the natural time variable for classical and quantum cosmology} Nucl. Phys. B449 (1995) 289, gr-qc/9405015.
With zero cosmological constant, there are two general classes of results;
A)- those that
follow from the methods of Rovelli, Borrisov
and Theimann, and
B)- those that follow from the
methods of Gambini, Pullin et al.
As mentioned these differ by operator ordering terms.
A) In the case of the ordering studied by Rovelli -and myself-, Borissov and Thiemann, there seems to be a problem of the kind just mentioned: 1) is satisfied, the theory is completely well defined, but 2) is not and the limit does not seem to have massless gravitons or other massless particles. There are several different manifestations of this problem. The finite hamitonian constraint operators commute too strongly, i.e. they are ultralocal and there is no defintion of energy in the asymptotically flat case which is both bounded from below and has massless particles in the spectrum. It is also the case that one can easily construct an infinite number of physical operators that commute with the hamiltonian constraints and with each other, showing that the state space has developed a large number of superselection sectors, which suggests that there is no long ranged propagation of information in the theory.
In the case B) of the results of Gambini, Pullin etc. some of these problems are resolved (see gr-qc/9909063). The algebra of the hamiltonian constraints is no longer ultralocal, and close on the diffeomorphism generators. There are some remaining issues concerning the regularization dependence of the commutators. Whether their ordering resolves the other problems is not yet known. I do not think we should be too disturbed by these result. No one is surprised if the quantization of the Yang-Mills equations leads to a theory that is well defined but does not have those equations as a classical limit. In a sense the phenomenon is the same in both cases, the classical theory has massless fields but, without special care taken the quantum theory only has massive or confined modes. What this means is that we have to work harder to find the form of the quantum theory whose large volume limit has massless modes, and is hence (because the gauge symmetry includes diffeomorphisms) general relativity. Different people have taken different approaches to attacking this problem and much of the present work is motivated by different ideas about how to do this. Although it is hard to judge now, these different approaches may not be mutually exclusive. I list some of them here:
1- Find an operator ordering which fixes all the problems. It is in fact easy to see that were a term of a certain form to be added to the quantum hamiltonian constraint the problems of being ultralocal and of there being no transmission of information would be avoided. The problem is that so far no one can derive this missing term from a rigorous regularization of the classical hamiltonian constraint, or show that its addition results in a good constraint algebra. Several people believe this can be accomplished by changing the inner product, or equivalently the precise space of states on which the operator acts. This is partly the motivation for the approach of Gambini and Pullin.
2- Fix the problem in the path integral formalism by putting the missing term directly in the path integral action. This has been advocated by Rovelli, who showed in his paper with Reisenberger (referenced above) that it emerges naturally in the path integral framework by changing the time ordering of the term which comes from the regularization of the hamiltonian constraint. What this means is that the regularization procedure must be carried out in a way that is covariant in space and time to get the right dynamics, and this is much harder to do in the hamiltonian framework than in the path integral framework, because operators at different times are very complicated to represent in the canonical framework. Reisenberger, and Barrett and Crane (referenced above) also have found forms for the action in spin foam that they get by direct translation of the classical action, without going throught the canonical formalism. In these the missing term needed for long ranged propagatation appears, which is evidence for Rovelli's view.
3- Fix the problem in the path integral framework by searching directly for the form of the action that leads to a good classical limit. This is analogous to the way one uses the renormalization group in statistical physics to search for the hamiltonians that describe phase transitions. I find this particlarly interesting because it allows us to investigate the general question of how path integrals are to be defined in a lorentzian theory in which the causal structure is a degree of freedom. Because of this there is not necessarily any well defined continuation from a Euclidean theory. If the limit exists such that 2) is good there must be a different kind of critical phenomena than the usual 2nd order phase transitions that are necessary to define conventional Euclidean quantum field theories. We have identified the appropriate analogoue, which is certain non-equilibrium critical phenomena associated with problems like directed percolation and the growth of soap bubbles. Markopoulou and I have worked in collaboration with people in those areas such as Per Bak, Maya Paczuski and Stuart Kauffman to apply the methods in that field to quantum gravity. Borissov and Gupta, and Gupta have results that confirm this general idea in 2+1 and 1+1 models. Very significant results along these lines were found recently by Abjorn, Loll and Anagnastopolous (referenced above). They find that one can define a convergent path integral for lorentzian 1+1 quantum gravity, which can be thought of as simple low dimensional examples of evolving spin network theory. Their results are quite surprising as they show a qualitatively different kind of behavior (technically, a new universality class) than exists in 2d euclidean quantum gravity models. Extensions of their results to higher dimension are under study by several people. (I might note that their results were characterized as the most interesting resutls of the last year in the summary talk of the lattic QFT conference in Pisa 2001). In very recent results they show that these lorentizan methods allow one to cross "the c=1" barrier, which has been a major stumbling block for non-perturbative approaches to string theory.
4- Hypothesize that strict quantization of the field equations of general relativity does not yield a theory whose classical limit is general relativity but that there may be a theory in the large class of diffeomorphism invariant QFT's that can be expressed in loop quantum gravity that will have a good classical limit that includes general relativity. One approach to this is to hypothesize that this can happen if the description of gravitons that results from the semiclassical limit matches that given by one of the infinite list of perturbative string theories. There are, in fact, general arguments that string-like excitations must appear as weakly coupled modes around any classical limit of loop quantum gravity.
This is the approach I have used to try to invent a form of the theory that also solves the main problem in string theory, which is to invent a background indepednent approach. The idea is that as string theory seems to provide the only consistent description of gravitons at a perturbative level, and as there are many perturbatively consistent string theories, perhaps any quantum theory of qravity that solves 2) will do it in a way that reproduces the main features of perturbative string theory. In a recent paper I showed that this strategy works, in the sense that there are choices of kinematics and dynamics for evolving spin networks such that one can show that, IF there is a semiclassical limit, that limit reproduces string theory, in the form of the matrix model.
The behavior of the solutions to the hamiltonian constraint with zero cosmological constant, with relevance to the classical limit were discussed from different points of view in: L.Smolin, {\it The classical limit and the form of the hamiltonian constraint in nonperturbative quantum gravity} preprint CGPG-96/9-4, gr-qc/9609034; R.Loll, gr-qc/9708025, Class.Quant.Grav. 15 (1998) 799-809; R.Gambini, J.Lewandowski, D.Marolf, J.Pullin, {\it On the consistency of the constraint algebra in spin network quantum gravity}, gr-qc/9710018, Int.J.Mod.Phys. D7 (1998) 97-109; J.Lewandowski and D.Marolf, Int.J.Mod.Phys. D7 (1998) 299-330, gr-qc/9710016; D.Neville, Phys.Rev. D59 (1999) 044032, gr-qc/9803066.
The connection between classical limits of lorentzian path integrals and non-equilibrium critical phenomena has been discussed in, F.Markopoulou and L.Smolin {\it Causal evolution of spin networks} gr-qc/9702025. CGPG preprint (1997), Nuclear Physics B, Nucl.Phys. B508 (1997) 409-430; R.Borissov and S.Gupta, {Propagating spin modes in canonical quantum gravity}, gr-qc/9810024; D.P.Rideout, R.D.Sorkin, {\it A Classical Sequential Growth Dynamics for Causal Sets}, gr-qc/9904062; A.Criscuolo, H.Waelbroeck, {\it Causal Set Dynamics: A Toy Model}, gr-qc/9811088; Class.Quant.Grav. 16 (1999) 1817-1832.
The connections to string theory are discussed in L.Smolin, {\em Strings as perturbations of evolving spin-networks}, hep-th/9801022, L.Smolin, {\it A candidate for a background independent formulation of M theory}, hep-th/9903166.
The direction of research in loop quantum gravity has changed rather strongly in the last few years. I think it is not unfair to compare it to QCD in the following way: loop quantum gravity is now a general framework for studying diffeomorphism invariant quantum field theories. It exists in both hamiltonian and path integral versions, and the kinematical structures as well as the relationship between them are by now well understood. The robust features of the dynamics are understood, and several different variations, differing by well understood operator ordering ambiguities, are under study. A variety of methods are in use, ranging from proofs of rigorous theorems to numerical studies. This framework can be used to study a large class of theories including quantum general relativity and supergravity in different dimensions. It took more than 10 years to work out this framework, but now that we have it attention has shifted to other questions:
1- How to take the semi-classical limit and how to choose the dynamics so that there is a semi-classical limit. This includes the different approaches I mentioned above. This is a hard problem, we should note that it is still not completely solved for QCD. But it is now as well defined in quantum gravity as it is in QCD and it is under attack from several directions, as I indicated. The recent results of Ambjorn, Loll, Anagnastopolou, Borissov, Gupta and others shows that definite results can be achieved for low dimensional systems and more work in this direction is underway. The recent paper of Gambini, Pullin and collaborators shows that this issue is very much alive also within the hamiltonian framework.
2- Working out of different examples, including different versions of supergravity, including antisymmetric tensor gauge fields, and quantum gravity in various dimensions, both lower and higher than 3+1.
3- Application to various problems of physical interest. The framework is sufficiently well understood to study various problems about which physical predictions can be made. Two under investigation are the description of black hole horizons and predictions for corrections to propagation of light in vacua, coming from the discrete stucture, because of claims that these could be observed astrophysically.
4- Relationship to other approaches. Now that the kimematical frameowrk is understood and a lot is known about the general form of the dynamics, we can investigate relationships to other approaches to quantum gravity. Several of these are in progress now:
-relationship to Topological Quantum Field Theory (TQFT). This is turning out to be quite important as I indicated, both because certain boundary conditions of interest induce boundary hilbert spaces connected to TQFT's and because the general structure of the actions for GR and supergravity is closely connected to certain TQFT's. One important outcome of this work is the idenficiation of a mathematical langauge which is common to loop quantum gravity, perturbative string theory and topological quantum field theory. This is the representation theory of quantum groups or, as it is sometimes called, the theory of modular tensor categories. This gives a mathematical langauge within which to seek the unification of string theory and loop quantum gravity.
-relationship to causal sets. This connection, invented by Markopoulou has led to the new attack on lorentzian path integrals, the first fruit of which we see in the results of Ambjorn, Anagnastopolous and Loll. There are also new results in causal set dynamics (by Rideout and Sorkin, and Criscuolo and Waelbroeck) that confirm our discovery of the analogy between the classical limit of theories with fluctuating causal structure and non-equilibrium critical phenomena such as directed percolation models.
-relationship to non-commutative geometry. This has been approached by Ashtekar and Zapata, who noticed that there is a sense in which quantum geometry in loop quantum gravity is non-commutative. It has also been studied by Rovelli and several collaborators.
-relationship to consistent histories. Once a path integral framework for loop quantum gravity was established it becomes natural to examine whether the consistent histories approach developed by Gell-Mann, Hartle and others can be applied to it. It turns out that this requires the precise mathematical formulation of consistent histories given by Isham and collaborators, which makes use of the langauge of topos theory. Markopoulou has shown that a related histories approach, called quantum causal histories, formulated in the same mathematical langauge, describes the structure of causally evolving spin networks. What both approaches have in common is that there is a structure (technically a pre-sheaf) consisting of many hilbert spaces and observables algebras, each connected with a subset of observables of the quantum cosmology. In Isham et. al. these correspond to the different consistent sets of histories, in Markopoulou these correspond to what is observable in the causal pasts of the different local observables in the spacetime. Under way is the examination of the relationship between these two appraoches.
It should be noted that the mathematics involved in both approaches is related to the langauge of modular tensor categories. I mentioned above, giving more evidence that this may be the right mathematical framework for the full theory of quantum gravity. I should note also that the approaches of Markopoulou and Isham, while different, each show some promise of giving a new formulation of quantum cosmology which resolves the foundational problems in that subject. I think it very striking that a mathematical structure that emerges from trying to make a sensible formulation of quantum cosmology that would apply to observations made by observers inside the universe is closely related to that which emerged from loop quantum gravity, TQFT and string theory.
-relationship to string theory. This is my main occupation now, there are some striking results already, such as the background independent formulation of (p,q) strings and SL(2,Z) duality we did with Markopoulou, (hep-th/9712148, Phys.Rev. D58 (1998) 084033), the general argument mentioned above that the perturbations of evolving spin networks involve stringlike degrees of freedom and a particular proposal for a background independent form of M theory.
Let me close by coming back to the two issues you mentioned, to make clear how they have been addressed:
The problem of gauge invariant gravitational observables:
First, at the level of spatially diffeomorphism invariant observables, a sufficient set has been constructed and diagonalized, in closed form, to label a complete basis of states in terms of their eigenvalues, for each of a large set of theories.
Concerning spacetime diffeomorphism invaraint observables, one does not expect to be able to do the same in closed form. In fact, one sign of the problem with the dynamics mentioned above is that one can, in fact, construct infinite classes of operators on the space of solutions Theimann discovered, that (by construction) commute with the quantum hamiltonian constraint and with each other (see papers by Loll under that discussion). I take this to be evidence there is not sufficient propagation of information in the theory. It is certainly to be expected that one sign of fixing the problem would be that it will no longer be possible to write such a large set of physical observables in closed form in the canonical theory.
On the other hand, it is not difficult to construct as many physical, spacetime difeomorphism invariant, observables as one likes in a histories framework. (This point has been emphasized for a long time by Hartle). This is the case in spin foam, as emphasized by Rovelli, Reisenberger, Baez and others. Once that is done one can work backwards and express those physical observables as canonical operators using Rovelli's formulation of projection operators on physical states (referenced above). The expectation values of the resulting operators are expressed as infinite series which, while not in closed form, are completely well defined.
Most importantly, this means that in spin foam or evolving spin networks, expectation values of physical, gauge invariant observables can be written down and explicitly computed, using either analytic or numerical approximation techniques. Examples in which this is carried out in detail in 1+1 cases are discussed in the papers of Ambjorn, Loll etc referenced above. Work is in progress to extend this first to 2+1 then to 3+1.
One can also construct physical operators by two other methods 1) fix the time gauge and then construct the normal hamiltonian theory for evolution in that time gauge. Diffeomorphism invariant observables are then promoted to physical observables, defined on spacelike slices picked out by the gauge conditions. This approach is described in detail in L. Smolin, {\it Time, measurement and information loss in quantum cosmology} in {\it Directions in general relativity, vol. 2 Papers in honor of Dieter Brill} ed. B. L. Hu and T. A. Jacobson (Cambridge University Press, Cambridge, 1993), gr-qc/9301016; C. Rovelli and L. Smolin, {\it The physical hamiltonian for non-perturbative quantum gravity}, with Carlo Rovelli, Phys. Rev. Lett. 72 (1994) 446-449, gr-qc/9308002.
Alternatively one can construct evolving constants of motion, as described in detail in several papers of Rovelli, and then evaluate them for the time variable set equal to zero, when they are equal to ordinary spacially diffeomorphism invariant observables. This is sufficient to promote the spectrum of the area and volume operators to physical observables.
The precise statement of the operator valued nonlinar field equations:
As mentioned above, we have precise regularization techniques that, given the classical hamiltonian constraint, return finite well defined quantum constraint operators. Those that arise from different regularization procedures differ by now understood operator ordering terms. There are no anomolies, in the sense of terms proportional to 1 that arise in their algebra; thus they have infinite dimensional spaces of solutions. The resulting theory is like QCD, completely well defined, but certain forms appear not to have a classical limit which reproduces the classical field equations. The operators that result from regularizations of the classical expression appear to be missing a certain term which it is known would lead to long ranged propagation.
There could be several reasons for this, which are all under investigation. 1) The missing term will result from a modification of the inner product on diffeomorphism invariant states (this is being investigated by Theimann, Gambini, Pullin and collaborators). 2) The missing term was lost by a regularization method that was not sufficiently covariant in both space and time; it can be easily reinserted by symmetrizing the path integral amplitude that corresponds to the canonical operator and could in principle be found also be a complicated procedure in the canonical theory that would involve point spliting in time and space (this is Rovelli's approach) 3) the condition that the quantum constraint operator must arise as the limit of the regularization of the classical expression is too strong, what is required is only that the expectation value of the expression reproduce the classical constraint, and the missing term may be added without changing the fact that this property is satisfied. In this case we are free to add it and study its consequences. 4) the theory of quantum gr does not in fact have a semiclassical limit which includes classical gr, but theories may exist which can be expressed in the same kinematical langauge which that will do this, and they may accomplish this by having not only classical gr, but a perturbative string theory, as their semiclassical limit.
As I indicated, research is going on in all of these directions. So to summarize the situation in loop quantum gravity can perhaps be usefully compared to QCD, which was after all the main inspiration for it.: there is a well understood and robust kinematical framework which allows us, as in QCD, to represent gauge invariant states and histories; there is both a canonical and path integral formalism which are related to each other in the same way as in QCD. The form of the quantum hamiltonian constraint is well understood, and an infinite dimensional space of solutions is known. The dynamics is also understood in the path integral langauge. As in QCD, the theory can be investigated by a whole spectrum of methods, including rigorous methods in constructive quantum field theory, point splitting regularization methods, series expansions (both strong and weak coupling) and numerical methods. As the framework is well defined the relationship between results found by these different methods can be compared. The different methods agree about certain striking physical predictions such as the discreteness of area and volume. There are, as in QCD, various versions of the theory, with and without supersymmetry, in different dimensions, with different matter degrees of freedom and with slightly variations in the forms taken for the hamiltonians and actions.
Finally, as in QCD, there are hard problems, still under investigation, concerning the behavior of the solutions to different versions of the theory at large scales.
NOTE (1): Quantum geometry: In theoretical physics, quantum geometry is the set of new mathematical concepts generalizing the concepts of geometry whose understanding is necessary to describe the physical phenomena at very short distance scales (comparable to Planck length). At these distances, quantum mechanics has a profound effect on physics. Each theory of quantum gravity uses the term quantum geometry in a slightly different fashion. String theory, the leading candidate for a quantum theory of gravity, uses the term quantum geometry to describe exotic phenomena such as T-duality and other geometric dualities, mirror symmetry, topology-changing transitions, minimal possible distance scale, and other effects that challenge our usual geometrical intuition. More technically, quantum geometry refers to the shape of the spacetime manifold as seen by D-branes which includes the quantum corrections to the metric tensor, such as the worldsheet instantons. For example, the quantum volume of a cycle is computed from the mass of a brane wrapped on this cycle. In an alternative approach to quantum gravity called loop quantum gravity (LQG), the phrase quantum geometry usually refers to the calculation within LQG that shows that certain physical observables, such as the area, have a discrete spectrum of eigenvalues. This phrase is often used as synonymous with loop quantum gravity as a whole. It is possible but considered unlikely by many that this strictly quantized understanding of geometry will be confirmed by string theory.
NOTE (2): Information Theoretic Entropy: The basic concept of entropy in Information Theory has to do with how much randomness there is in a signal or in a random event. An alternative way to look at this is to talk about how much information is carried by the signal. As an example consider some English text, encoded as a string of letters, spaces and punctuation (so our signal is a string of characters). Since some characters are not very likely (e.g. 'z') while others are very common (e.g. 'e') the string of characters is not really as random as it might be. On the other hand, since we cannot predict what the next character will be, it does have some 'randomness'. Entropy is a measure of this randomness, suggested by C.E.Shannon in his 1949 paper "A Mathematical Theory of Communication". Shannon derives his definition of entropy from the assumptions that:
The measure should be continuous. I.e. changing the value of one of the probabilities by a very small amount should only change the entropy by a small amount. If all the outcomes (letters in the example above) are equally likely then increasing the number of letters should always increase the entropy. We should be able to make the choice (in our example of a letter) in two steps, in which case the entropy of the final result should be a weighted sum of the entropies of the final result. Shannon defines Entropy in terms of a discrete random event x, with possible states 1..n as:
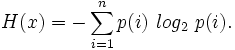
That is the entropy of the event x is the sum over all possible outcomes i of the product of the probability of outcome i times the log of the probability of i. We can equally apply this to a probability distribution rather than a discrete-valued event. Shannon shows that any definition of entropy satisfying his assumptions will be of the form:
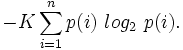
Where K is a constant (and is really just a choice of measurement units).
NOTE (3): T-duality: T-duality is a symmetry of string theory, relating type IIA and type IIB string theory, and the two heterotic string theories. T-duality transformations act on spaces in which at least one direction has the topology of a circle. Under the transformation, the radius R of that direction will be changed to 1/R, and "wrapped" string states will be exchanged with high-momentum string states in the dual theory. For example, one might begin with a IIA string wrapped once around the direction in question. Under T-duality, it will be mapped to a IIB string which has momentum in that direction. A IIA string with a winding number of two (i.e., wrapped twice) will be mapped to a IIB string with two units of momentum, and so on.
The total squared mass of a closed string
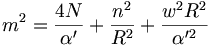
is invariant under the exchange 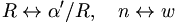 ,
,
and the interactions and all other physical phenomena can be proved invariant under this operation, too. T-duality acting on D-branes changes their dimension by +1 or -1.
Andrew Strominger, Shing-Tung Yau, and Eric Zaslow have showed that mirror symmetry can be understood as T-duality applied to three-dimensional toroidal fibres of the Calabi-Yau space.
Utenti connessi...:
CHANDRAst (midi by CHANDRAst 2004)