Puo' succedere di aver fatto un rilievo, e di non aver gli strumenti
per stenderlo graficamente (la carta millimetrata, il goniometro,
la squadretta, etc.), eppure di voler saper quanta si e` scesi
oppure quanto ci si è spostati in pianta.
Con un po' d'esperienza si riesce a fare una stima grossolana
dell'andamento della grotta solo guardando le misurazioni.
Se peró si vuole una valutazione piu` precisa, occorre fare
qualche conto numerico.
Questi conti non sono difficili: traducono numericamente le
operazioni che vangono effettuate graficamente durante la stesura
del rilievo, e sono alla base di tutti i programmi per la
stesura automatica dei rilievi.
Si basano su semplici formule di trigonometria piana (spiegate
più sotto).
Questa sezione include, come riferimento,
una tabella dei valori delle funzioni trigonometriche.
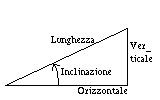
A partire dai dati di Distanza (bindella),
e Inclinazione (clinometro),
si possono calcolare le componenti Orizzontale
e Verticale della sezione utilizando
le formule:
"cos" (coseno) e "sen" (seno) sono due funzioni trigonometriche i cui valori,
per angoli compresi fra 0 e 90 gradi, sono
riportati nella tabella alla fine della sezione.
E se una inclinazione e` negativa? Dovete ricordarvi che
Attenzione al segno: nell'esempio la misurazione 3-4 ha Inclinazione
negativa (percio` il caposaldo 4 si trova piu` in basso rispetto
al caposaldo 3), quindi la componente Verticale e` negativa.
La componente Orizzontale e` "sempre" positiva. (Perche`?).
Da notare che quando l'inclinazione e' 90 gradi l'Orizzontale
e` zero (nell'esempio la misurazione 4-5).
Questi numeri rappresentano la posizione, in sezione,
relativa dei capisaldi, due a due.
Con questi dati si puo` valutare le posizioni dei vari capisaldi
relativamente ad uno di essi, per esempio il primo, numero 1: per il 2
non occorre fare nulla; per il 3 basta sommare la sua posizione
relativa a 2 a quella di 2 rispetto a 1.
Per il 4 si procede analogamente, stando attenti al segno!
Ecco il risultato:
Quindi complessivamente siamo saliti di 17.61 metri.
La componente Orizzontale non ci dice molto; tuttalpiu` serve
per valutare quanto deve essere grande il foglio di carta millimetrata
su cui disegneremo poi la sezione.
Per sapere quanto ci siamo spostati in pianta, dobbiamo riprodurre
numericamente le operazioni che si eseguono disegnando la pianta.
A tale scopo usiamo la distanze Orizzontali e la Bussola.
Nord = Orizzontale cos(Bussola)
Est = Orizzontale sen(Bussola)
"cos" e "sen" sono le stesse funzioni trigonometriche di prima.
Peró ora c'e` un'altra complicazione: le misure della bussola
vanno da 0 a 360 gradi, e nelle tabelle le funzioni sono elencate
solo per angoli fra 0 e 90 gradi. Il motivo di cio` e` dovuto alle
seguenti relazioni (che permettono di trovare i valori delle funzioni
per tutti i gradi):
(se non fosse per i segni sarebbero facili da ricordare).
Dunque riprendiamo il nostro esempio e calcoliamo le distanze nelle
componenti Nord ed Est della pianta:
PUNTI Nord Est
1 - 2 5.51 11.29
2 - 3 6.26 1.56
3 - 4 - 9.85 16.40
4 - 5 0.00 0.00
Da notare che 3-4 ha una componente Nord negativa: la direzione
121-Nord indica che la galleria sta' andando verso sud-est!
Ancora: 4-5 ha entrambe le componenti zero: infatti e` un pozzo, e non
da` alcun spostamento in pianta.
Adesso valutiamo gli spostamenti relativamente al caposaldo 1:
. Spostamento Spostamento
PUNTI Nord Est
1 - 2 5.51 11.29
2 - 3 11.77 12.85
3 - 4 1.89 29.25
4 - 5 1.89 29.25
Finalmente possiamo dire che ci
siamo spostati di poco meno di due metri verso nord, ma di quasi trenta
(29,25 per l'esattezza) verso est.
Tabella dei valori delle funzioni trigonometriche.
