Dispensa n.12 - Equazione fondamentale della statica dell'atmosfera.
Sommario: in questa dispensa osserveremo da vicino come
si giunge ad impiantare l'equazione fondamentale della statica dell'atmosfera.
Vi ricordate di cosa si occupa, in fisica, la statica ? E'
quella parte della cinematica che si occupa del comportamento dei corpi in
quiete.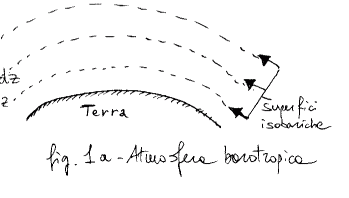
In meteorologia si considera, per semplificarne lo studio,
un'atmosfera teorica in quiete rispetto alla Terra, ovvero priva di moti,
e le cui superfici isobariche sono tutte parallele alla superficie terrestre
considerata priva di rugosità (il che equivale a dire che, considerato un punto
qualsiasi appartenente ad una determinata superficie isobarica, l'altezza
rispetto alla superficie considerata piana sarà sempre la medesima). Tale atmosfera viene definita barotropica
(figura 1a). Se le superfici isobariche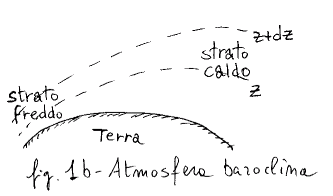 vengono invece considerate inclinate
, come avviene normalmente in natura a causa delle differenze di temperatura e
di densità tra strato e strato, si parla di atmosfera baroclina (figura
1b). vengono invece considerate inclinate
, come avviene normalmente in natura a causa delle differenze di temperatura e
di densità tra strato e strato, si parla di atmosfera baroclina (figura
1b).
L'equazione che cerchiamo parte proprio dall'atmosfera
barotropica.
Piccolo cenno (senza pretese) alla simbologia matematica.
Nelle matematiche, per indicare variazioni piccolissime di una
grandezza, ossia variazioni "infinitesimali", così piccole da non
poter essere espresse da alcun numero, per quanto piccolo, si usa la lettera d
seguita dal simbolo della variabile che subisce le variazioni. La potenza del
calcolo infinitesimale consiste nel generalizzare le leggi fisiche, sollevandole
dal "peso" dei numeri.
Esempio:
con p si indica solitamente la pressione; una
piccolissima, minutissima variazione di pressione si indicherà dp;
se con z indichiamo una lunghezza, dz indicherà
una sua variazione infinitesimale.
Se da valori infinitamente piccoli si vuole passare a differenze
finite ovvero rappresentabili con numeri, useremo la lettera greca maiuscola D
(delta). Perciò Dp rappresenterà una
definita variazione di pressione.
Ed ora, avanti tutta con l'equazione...
Cominciamo col considerare una superficie isobarica posta ad una
quota z rispetto alla superficie terrestre (figura 2).
Un piccolo incremento di quota, dz, ci farà innalzare
alla superficie isobarica posta a z + dz (figura 3). Dai nostri
precedenti studi sappiamo che  la pressione diminuisce man mano che ci si
allontana dalla Terra. Per cui, se alla quota z + dz essa è p,
alla quota z (più vicina alla Terra) la pressione sarà leggermente più
alta, ovvero sarà p + dp (figura 4). la pressione diminuisce man mano che ci si
allontana dalla Terra. Per cui, se alla quota z + dz essa è p,
alla quota z (più vicina alla Terra) la pressione sarà leggermente più
alta, ovvero sarà p + dp (figura 4).
Riassumendo, avremo:
 |
alla quota z, la pressione p + dp
|
 |
alla quota z + dz, la pressione p.
|
Quando abbiamo studiato la distribuzione 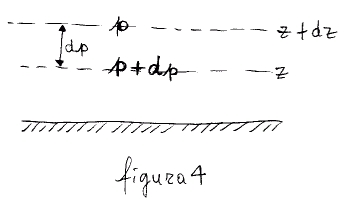 della pressione al
suolo, abbiamo visto che, se esiste una differenza di pressione, esiste anche
una forza, chiamata di gradiente, che è orientata dalle alte verso le basse
pressioni (figura 5). della pressione al
suolo, abbiamo visto che, se esiste una differenza di pressione, esiste anche
una forza, chiamata di gradiente, che è orientata dalle alte verso le basse
pressioni (figura 5).
Esaminiamo ora un cilindretto d'aria con base unitaria, faccia
inferiore posta 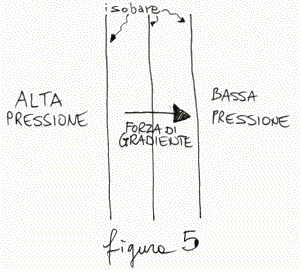 alla quota z, e quella superiore alla quota z
+ dz (figura
6). alla quota z, e quella superiore alla quota z
+ dz (figura
6).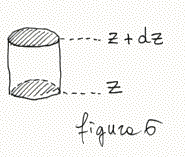 Trovandosi le due facce a quote differenti, la pressione sarà differente su
ciascuna delle due facce, e precisamente sarà più elevata sulla faccia
inferiore (p + dp) e minore sulla faccia superiore (p) (figura 7). Trovandosi le due facce a quote differenti, la pressione sarà differente su
ciascuna delle due facce, e precisamente sarà più elevata sulla faccia
inferiore (p + dp) e minore sulla faccia superiore (p) (figura 7).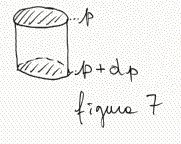
Poichè tra le due facce del cilindretto esiste una differenza
di pressione, vi sarà pure una forza di gradiente G, diretta
verticalmente da z verso z + dz, ovvero dalla pressione p + dp
verso la pressione p (figura 8).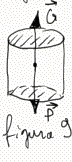
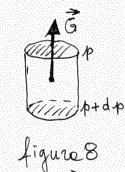 E qui arriviamo al bello. Se è vero che il cilindretto è in
quiete, ed è vero perchè siamo partiti proprio da questo presupposto, se
esiste questa forza G, vi dovrà essere una forza di uguale intensità
che si contrappone ad essa. Questa forza esiste, ed è la forza peso P,
diretta verticalmente verso il basso (figura 9). E qui arriviamo al bello. Se è vero che il cilindretto è in
quiete, ed è vero perchè siamo partiti proprio da questo presupposto, se
esiste questa forza G, vi dovrà essere una forza di uguale intensità
che si contrappone ad essa. Questa forza esiste, ed è la forza peso P,
diretta verticalmente verso il basso (figura 9).
Possiamo esprimere questa contrapposizione scrivendo:
G = -P
|
(c'è il segno meno, poichè abbiamo detto che sono uguali
in intensità, ma di verso opposto)
|
La grandezza di G è espressa proprio dalla differenza di
pressione, ovvero dp.
Parlando di forze, l'equazione fondamentale della dinamica ci
può senz'altro aiutare. Essa dice che una forza F è pari alla massa m
per l'accelerazione a:
F = m * a
Il peso di un corpo, essendo una forza, può essere espressa
con
P = m * g
dove g è l'accelerazione di gravità.
Ci piacerebbe esaminare la forza peso di un corpo in relazione
alla sua densità: come possiamo fare ?
Basta ricordare che la densità esprime il rapporto tra massa e
volume in cui tale massa è contenuta:
d = m / V.
Con un piccolo artificio matematico a tutti noi noto, possiamo
ricavarci dalla formula precedente la massa, e cioè:
m = d * V
Perciò possiamo scrivere:
P = m * g
e sostituire m con la relazione trovata:
P = d * V * g.
Così facendo siamo riusciti ad esprimere la forza peso P
in funzione della densità del corpo anzichè della sua massa. Dalla espressione
ricavata si vede chiaramente che se aumenta la densità aumenterà la forza peso
(proporzionalità diretta).
Torniamo al nostro cilindretto.
Se la base è unitaria (cioè uguale a 1), il suo volume V
sarà dato dal prodotto
area della base * altezza
ovvero
V = 1 * dz = dz
Pertanto
P = d * V * g
sostituendo
V con dz, diventerà
P = d * dz * g.
Ora
abbiamo tutto ciò che ci serve per creare la nostra equazione:
G
= dp
P = d * g * dz
per cui, se G
= -P
che rappresenta l'equazione fondamentale della statica
dell'atmosfera, ovvero la legge che governa il cilindretto d'aria in quiete.
Il
gradiente barico verticale sarà dato da:
dp / dz = -d * g
che
rappresenta la legge di diminuzione della pressione al crescere dell'altezza. In
termini di differenze finite possiamo scrivere
Dp
= -d * g * Dz.
Considerazioni
Dall'esame dell'equazione che esprime il gradiente barico
verticale
dp / dz = -d * g
possiamo
trarre alcune considerazioni.
dp / dz lega la variazione
di pressione alla variazione di altezza. Questa variazione dipende dalla
densità e dall'accelerazione di gravità, che può essere assunta come
costante. Per cui si può concludere dicendo che la pressione varia lungo la
verticale in funzione della densità e, in definitiva, in relazione alla
temperatura dell'aria.

(rev.01/2001) |
 della pressione al
suolo, abbiamo visto che, se esiste una differenza di pressione, esiste anche
una forza, chiamata di gradiente, che è orientata dalle alte verso le basse
pressioni (figura 5).
della pressione al
suolo, abbiamo visto che, se esiste una differenza di pressione, esiste anche
una forza, chiamata di gradiente, che è orientata dalle alte verso le basse
pressioni (figura 5). alla quota z, e quella superiore alla quota z
+ dz (figura
6).
alla quota z, e quella superiore alla quota z
+ dz (figura
6).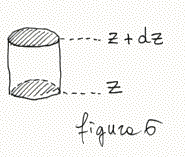 Trovandosi le due facce a quote differenti, la pressione sarà differente su
ciascuna delle due facce, e precisamente sarà più elevata sulla faccia
inferiore (p + dp) e minore sulla faccia superiore (p) (figura 7).
Trovandosi le due facce a quote differenti, la pressione sarà differente su
ciascuna delle due facce, e precisamente sarà più elevata sulla faccia
inferiore (p + dp) e minore sulla faccia superiore (p) (figura 7).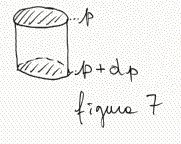

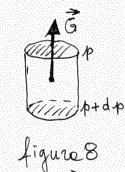 E qui arriviamo al bello. Se è vero che il cilindretto è in
quiete, ed è vero perchè siamo partiti proprio da questo presupposto, se
esiste questa forza G, vi dovrà essere una forza di uguale intensità
che si contrappone ad essa. Questa forza esiste, ed è la forza peso P,
diretta verticalmente verso il basso (figura 9).
E qui arriviamo al bello. Se è vero che il cilindretto è in
quiete, ed è vero perchè siamo partiti proprio da questo presupposto, se
esiste questa forza G, vi dovrà essere una forza di uguale intensità
che si contrappone ad essa. Questa forza esiste, ed è la forza peso P,
diretta verticalmente verso il basso (figura 9).![]()