 A titolo di esempio consideriamo la situazione in figura a destra.
L'errore quadratico e`
A titolo di esempio consideriamo la situazione in figura a destra.
L'errore quadratico e`
A.Vanin, R.Murgolo, M.Miragoli, "Un software per la speelologia",
Speleologia N. 28 (1993) p. 45-48
C.Chabert, R.A.Watson, "Mapping and measuring caves: a conceptual analysis",
Bull. Nat. Speleol. Soc. N. 43 (1981) p. 3-11
V.A.Schmidt, J.H.Schelleng, "The application of the method of Least squares
to the closing of multiconnected loops in cave geological surveys",
Bull. Nat. Speleol. Soc. N. 32 (1970) p. 51-58
G. Donzellini, "Un ambiente grafico interattivo per il trattamento di
poligonali", Conv. Naz. Speleo., Chiusa 1998
G.Donzellini, "Compensazione automatica degli errori di richuisone delle
poligonali con anelli multipli", Conv. Naz. Speleol., Chiusa 1998.
L.Fish, "More discussion on least square loop closure",
http://www.fountainware.com/compass/compart2.htm
Toporobot
http://www.geo.unizh.ch/~heller/toporobot/
UIS: Cave Survey and Mapping
http://rubens.its.unimelb.edu.au/~pgm/uisic/wgsurmap.html
Compass: programma di stesura rilievi
http://www.fountainware.com/compass/
Survex: programma di stesura rilievi
http://www.survex.com/
In internet sono disponibili parecchi programmi per l'elaborazione e la resa dei dati di rilievo. La Western Kentucky University ha una lista di programmi alla pagina http://www2.wku.edu/www/geoweb/karst/survey_programs/.
Il programma piu` conosciuto e` Toporobot, http://www.geo.unizh.ch/~heller/toporobot/Francais/index.html.
Non penso che ci sia un programma di elaborazione dei dati topografici decisamente migliore di altri. In generale un "programma di rilievo" e` concettualmente abbastanza semplice: le operazioni matematiche da eseguire per stendere un rilievo sono perlopiu` banali a livello di programmazione.
Quello che segue e` un tentativo di elenco, non esaustivo, delle problematiche che possono essers affrontate in un programma di rilievo.
Molto e` stato e viene fatto per definire le metodologie di topografia ipogea in un contesto tradizionale. Questi lavori sono giustamente orientati alla presa dei dati (in modo da garantire l'oggetivita` di un approccio scientifico), e alle convenzioni grafiche nella resa dei rilievi (per facilitare lo scambio delle informazioni).
L'Unione Speleologica Internazionale e` molto sensibile verso la definizione di standard per l'interscambio dei dati e delle informazioni a livello internazionale. E sta` decisamente facendo un ottimo lavoro in questo senso. Purtroppo (o perfortuna) manca la spinta commerciale che sostiene i tentativi di standardizzazione in molti altri campi; percio` queste iniziative procedono lentamente e con una impostazione semi-amatoriale.
Il problema degli anelli chiusi nella topografia ipogea e` che quando c'e` un anello si arriva allo stesso punto seguendo due percorsi differenti, e in generale le poligonali dei due percorsi portano a due punti distinti sulla carta, ma che corrispondono allo stesso punto nella realta`.
Questo e` dovuto alla presenza di errori nelle misurazioni:
Per cui le poligonali sono affette da errori. Quando non ci sono cicli questo viene solitamente ignorato (in topografia ipogea); pero` quando ci sono anelli risulta che le poligonali non si chiudono, percio` occorre distribuire l'errore per far tornare il rilievo. Nel far cio` non si imbrogliano i dati, ma si tiene in effetti conto dell'ulteriore informazione che due punti su due pezzi di poligonale differenti devono coincidere.
Il metodo dei minimi quadrati e` utilizzato per compensare gli errori in anelli chiusi. Esso permette di trovare la posizione statisticamente piu` significativa quando ci sono piu` percorsi che portano allo stesso punto (anelli chiusi). Esso consiste nel scegliere il valore che minimizza l'errore quadratico medio delle misure. Il metodo dei minimi quadrati e` molto semplificato nel rilievo ipogeo, poiche` in genere tali rilievi contengono solo traversamenti e non triangolazioni ne` trilaterizzazioni. Percio` la matrice che esprime la geometria e` molto semplificata e contiene, in genere, solo due elementi non nulli per ogni riga, e precisamente con valori +1 e -1.
La media pesata
La media pesata e` una procedure per stabilire che valore assegnare ad una certa quantita` avendo a disposizione piu` misurazioni di essa, ognuna con un certo grado di precisione. Nel caso di un anello chiuso, che coordinate assegnare al punto finale avendo due poligonali che lo raggiungono.
La covarianza e` l'espressione numerica del grado di precisione quando la quantita` e` un vettore X. Nel caso ad una componente (un solo numero) la covarianza si riduce alla varianza, che e` pari al quadrato della deviazione standard. Il peso associato ad una misura e` l'inverso della covarianza:
Date n misure di X: X1, ..., Xn, con covarianze C1, ..., Cn, e pesi Wk espressi come sopra, il valore di X che minimizza l'errore quadratico medio,
risulta la media ponderata:
Un traversamento (senza giunzioni) si comporta come una singola misura
con covarianza (supponendo le misure indipendenti)
La soluzione del problema dei minimi quadrati e` dunque una media pesata.
Distribuzione proporzionale
Si tratta di distribuire una certa quantita` D in n gruppi, ognuno con una capacita` mk. Questo serve per distribuire l'errore fra le varie tratte che compongono un ramo di poligonale. La soluzione e` simile alla media pesata: il gruppo k riceva una parte
Linearizzazione
I dati sono misurati con coordinate distanza D, azimuth A, e inclinazione I. Quando sono resi sulla carta si trasformano in coordinate ortogonali (est X, nord Y, e quota Z)
Questa trasformazione non e` lineare. Invece il metodo di aggiornamento dei minimi quadrati presuppone un probelma lineare. Questo significa che se i dati non sono vicini al problema originale la soluzione puo` essere molto diversa dalla posizione reale.
Conoscendo gli errori su D, A ed I si possono valutare quelli si X, Y e Z. Le covarianze nei due sistemi di coordinate misure sono legate dallo Jacobiano, J = d(X,Y,Z) / d(D,A,I) della trasformazione:
Lo Jacobiano risulta (questa espressione presuppone gli angoli espressi in radianti)
| cos(I) sin(A) | D cos(I) cos(A) | - D sin(I) sin(A) |
| cos(I) cos(A) | - D cos(I) sin(A) | - D sin(I) cos(A) |
| sin(I) | 0 | D cos(I) |
Tuuto cio` e` importante perche` quando calcolo la covarianza di un pezzo di poligonale posso sommare le covarianze delle singole tratte se queste sono espresse in un sistema ortogonale.
Da notare che lo Jacobiano diventa singolare quando l'inclinazione e` verticale (+/- 90o). Infatti in tal caso l'azimuth risulta indeterminato. Ne segue che in tal caso si hanno matrici di covarianza singolari. l'errore in Z e` pari a quello sulla distanza, mentre gli errori in X e Y restano incerti (anche se proporzionali a D e all'errore su I) poiche` A e` indefinito. Mediando sui valori dell'azimuth possimao usare la covarianza
[FIXME
L'errore sull'azimuth dipende dall'inclinazione.
...
]
Supponiamo di avere N cicli fondamentali, contenenti
K+1 punti (capisaldi). I punti indipendenti sono K
dato che uno di essi puo` essere arbitrariamente posizionato.
Esiste una relazione (di Eulero) fra il numero di cicli, il numero di punti
e il munero T di tratte (supponendo che ogni punto appartenga a due o
a tre tratte):
L'impostazione del sistema di equazioni non e` complicata, ma solo laboriosa. Esso si riduce alla forma
dove la prima somma e` estesa atutte le tratte entranti nel punto
Xj, e la seconda e` estesa alle tratte uscenti da esso.
Il coefficiente Mjj e` la somma dei pesi delle tartte entranti ed
uscenti da Xj.
Quando gli indici sono differenti il coefficiente Mij
e` pari a -Wk, l'opposto del peso della tratta che
collega il punto Xi al punto Xj,
ed e` nullo se i due punti non sono direttamente collegati.
[FIXME QUESTE "REGOLE" SONO DA VERIFICARE]
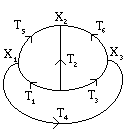
 A titolo di esempio consideriamo la situazione in figura a destra.
L'errore quadratico e`
A titolo di esempio consideriamo la situazione in figura a destra.
L'errore quadratico e`
Quindi il sistema diventa
| | | W1 + W5 + W4 | - W5 | - W4 | | | | | X1 | | | | | W1 T1 - W4 T4 - W5 T5 | | | |
| | | - W5 | W2 + W5 + W6 | - W6 | | | | | X2 | | | | | W2 T2 + W6 T6 + W5 T5 | | | |
| | | - W4 | - W6 | W3 + W4 + W6 | | | | | X3 | | | | | W2 T2 + W4 T4 - W6 T6 | | |
Correzioni di errori macroscopici
Il metodo dei minimi quadrati stima le correzioni delle singole misure in base ai loro pesi (che sono stimati o calcolati a partire dalle precisioni delle misure). Se le correzioni eccedono la precizione delle misurazioni (cioe` l'errore statistico) allora c'e` un errore macroscopico nei dati (nella lettura degli strumenti o nella scrittura dei dati). In tal caso si dovrebbe rifare il rilievo. In alternativa si puo` cercare di distribuire l'errore grossolano sul tratto di poligonale interessato, evitando di propagarlo (limitatamente) al resto del rilievo della grotta. Per far cio` si ricalcolano i pesi usando gli errori precedentemente calcolati, cioe` quelli che compensano l'errore macroscopico. In tal modo la misura con una grande errore riceve un peso molto basso e la sua influenza sul resto del rilievo viene ridotta.
Se c'e` un solo anello questo non ha effetto. Tuttavia nel caso di anelli multipli tutto cio` e` molto importante.
http://www.cc.utah.edu/~nahaj/cave/survey/internal-angles_example.html
Avendo a disposizione misure in eccesso (cioe` sia dal caposaldo A al
caposaldo B, che viceversa) e` possibile correggere le misure degli azimuth
compensando l'anomalia magnetica locale.
[FIXME a meno di una costante ???]
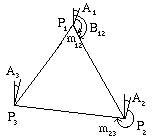 Per esempio consideriamo un triangolo con vertici P1
P2 e P3.
Supponiamo che le anomalie (incognite) nei tre punti siano
A1, A2, e A3.
Pertanto, per esempio, se da P1 a P2 misuriamo
m12 l'angolo effettivo con nord magnetico e`
b12 = m12 + A1.
Per esempio consideriamo un triangolo con vertici P1
P2 e P3.
Supponiamo che le anomalie (incognite) nei tre punti siano
A1, A2, e A3.
Pertanto, per esempio, se da P1 a P2 misuriamo
m12 l'angolo effettivo con nord magnetico e`
b12 = m12 + A1.
L'angolo P2P3P1 vale allora
Utilizzando il fatto che bij-bji= +/- 180o si ottiene un sistema di tre equazioni in tre incognite. Pero` questa tre equazioni non sono indipendenti, essendo la loro somma una relazione che deve sussistere fra le misure.
La valutazione delle somme degli angoli interni dei triangoli permette di rilevare macroscopici errori di lettura dei dati (nell'ipotesi di avere misurazioni sufficientemente ridondanti). Vedi P.R.Wolf e C.D.Ghilani "Adjustment Computations, Statistics and Least Squares in Surveing and GIS", Wiley 1997.
E` possibile quindi trovare la differenza fra anomalie locali in due punti a partire da queste equazioni.