Benché  il pendolo sia uno strumento molto semplice nel corso del tempo ha dimostrato e dimostra  nelle sue innumerevoli  varianti  una straordinaria utilità  nella comprensione e nell'analisi di diversi fenomeni fisici.

Nel 1851 si sapeva di già che la terra girasse, tuttavia ulteriore conferma a tale teoria venne nello stesso anno dal trentaduenne francese Leon Foucault  che con una geniale intuizione sorprese  i parigini e in breve tempo tutto il mondo. "Siete invitati a venire a   vedere girare la terra ..." disse a quelli che sarebbero stati i suoi "spettatori".

Egli, dopo diversi  esperimenti, giunse a costruire nel  Pantheon di Parigi un pendolo sospendendo internamente alla cupola dell'edificio,  per mezzo di un cavo d'acciaio del diametro di  1.4 mm e della lunghezza di  67 m, una sfera metallica dalla massa
m = 28 Kg facendo in modo che il centro di sospensione fosse libero di ruotare in quasi totale assenza di attrito.  

Egli spostò poi la massa di un angolo di circa 6° dalla sua posizione di equilibrio e legò la sfera ad un sostegno con una funicella che lasciò bruciare sulla fiamma di una candela: in questo modo quando la funicella si sarebbe rotta il pendolo avrebbe iniziato ad oscillare con una velocità iniziale  V₀ = 0.

  Foucault  aveva inoltre  cosparso il pavimento con della sabbia;  la sfera era provvista di una punta sporgente verso il basso che disegnava volta su volta su tale strato la traiettoria del pendolo.
Ora, se la terra non girasse, la traiettoria disegnata dall'asticella sarebbe dovuta essere sempre la stessa, di fatto, come lo studioso aveva previsto, le cose non andarono così: durante un tempo di osservazione di circa 6 ore durante il quale fu registrata un'oscillazione massima di 6 m  e il periodo di 16.5 s  e un pressoché lieve ma costante cambiamento della traiettoria. Di volta in volta l'asticella disegnava delle rette che rispetto alla traiettoria originale iniziarono ad essere visibilmente ruotate.

In parole povere mantenendo il  pendolo in oscillazione per 
31 h 47 m 33 s  l'asticella  spazzò un intero angolo giro.

Tale fenomeno confermava la continua rotazione terrestre: il piano di oscillazione del pendolo rimaneva invariato, mentre era la Terra a girare intorno al sistema che ,di fatto, non era solidale con essa perché  libero di ruotare intorno al suo centro di sospensione. La rotazione del piano avvenne in verso opposto a quello di rotazione della Terra, cioè da Est verso Ovest attraverso il Sud.

Il fatto che l'angolo giro sia stato spazzato in  31 h 47 m 33 s  potrebbe destare delle perplessità in quanto il tempo di rotazione terrestre è  di  24 h.

 Bisogna però considerare che il valore v_{p ,}della velocità angolare del piano di rotazione del pendolo, dipende dalla latitudine a cui esso si trova ed è uguale al prodotto della velocità angolare della terra v_t  per il seno della latitudine j del luogo di osservazione, cioè
v_p =  v_t sen j .

L'effetto è logicamente più pronunciato al Polo Nord, dove la velocità angolare del piano del pendolo coincide con quella terrestre,
cioè v_p =  v_T . Infatti per un  punto situato al  polo Nord  la
latitudine j = 90° e sen 90° = 1.
Al polo Nord il pendolo fa un giro completo ogni 24 ore perchè il suo piano ruota di 360° ogni 24 ore .

La velocità angolare del piano di rotazione del pendolo situato ad una latitudine intermedia diminuisce perchè la latitudine
j < 90° e sen j  < 1 .
Alla latitudine di Parigi ( + 48° 50' )  una rotazione completa del pendolo si compie in  31 h 47 m 33 s, mentre a Milano ( +45° 28' ) in 33 h 34 m 35 s.
Per determinare l'ampiezza a dell'angolo di rotazione apparente del piano di oscillazione del pendolo ad una latitudine j, basta applicare la formula
                       a = 360°·sen j .
In Italia il piano ruota ogni giorno di circa 254° e compie una rotazione completa in circa 34 ore.
All'equatore la velocità angolare del piano di rotazione del pendolo è nulla perchè la latitudine j = 0° e sen 0° = 0 così il piano di oscillazione non si muove e non si nota alcuna rotazione.

Immaginiamo che la penna sia il pendolo e il  blocchetto il pavimento solidale con la Terra. Facciamo partire la penna che "oscilla" sempre sullo stesso piano mentre il blocchetto gira insieme alla terra.......dopo un  determinato periodo di tempo la penna avrà spazzato un angolo giro e il risultato sulla carta sarà:

Un pendolo ben costruito, oltre all’isocronismo delle piccole oscillazioni, ha l’importante caratteristica di oscillare in un piano invariato nel tempo.

Il fatto che la sfera abbia spazzato un angolo giro pertanto è indice della rotazione terrestre non solo perché il pavimento è solidale con la Terra, come intuitivamente si potrebbe dire, ma soprattutto questo implica l’intervento di una forza trasversale che faccia ruotare tale piano, forza che identifichiamo con la F_c.

Supponiamo, ponendoci in una condizione ideale, di disporre di un pendolo che abbia  il punto di sospensione sul polo Nord e di farlo oscillare in un piano perpendicolare ad un piano tangente (a) alla calotta polare e parallelo al piano equatoriale. La massa oscillerà per  effetto della componente della forza peso tangente alla traiettoria  di velocità V_R (velocità radiale); componendo tale velocità con la w, perpendicolare, come noto, ad a, otteniamo, con la regola della mano destra che la F_c agisce da Est verso Ovest  quando m si muove lungo l’arco AB  e da Ovest verso Est quando m si muove lungo l’arco BA.(fig1).

È ovvio che maggiore è V_R , maggiore sarà F_c  che agirà secondo lo schema indicato in figura 2 causando il movimento di m lungo la traiettoria (fig3) osservata da Foucault.  

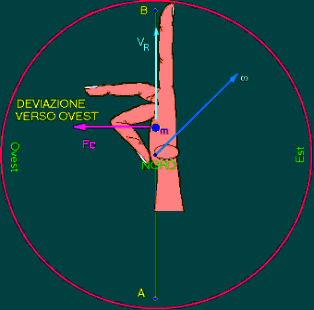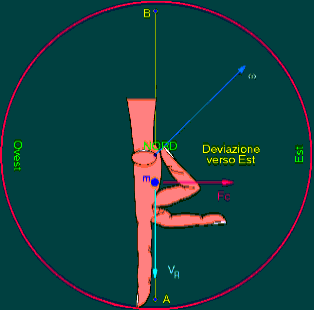figura 1: regola della mano destra

Nella Fotografia in alto è ripresa la base del sistema costruito da Foucault e la sfera in oscillazione

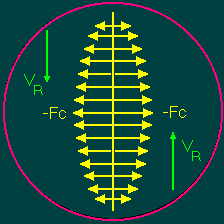
figura 2 : Schema forza


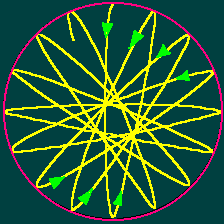
figura 3 : Rosone

                                                    -| Curiosità |-        -| Credits |-