Il pendolo è una dispositivo fisico semplicissimo costituito da un grave di massa  m  sospeso  per mezzo di un filo inestensibile  la cui estremità libera è solitamente  legata  ad un sostegno.

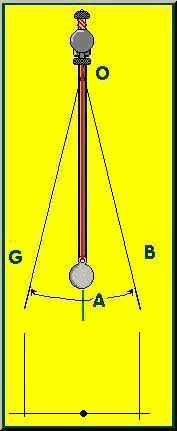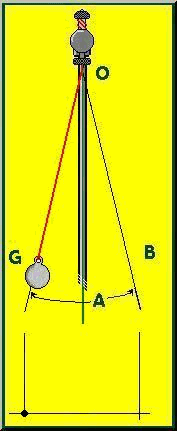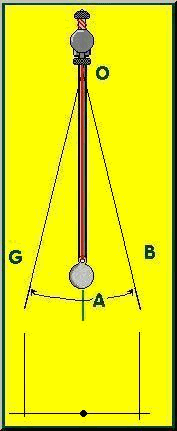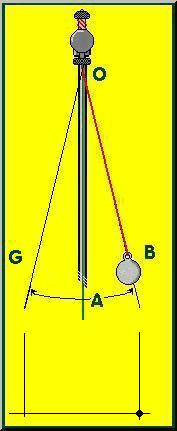
Indicato con “O” , il  centro di sospensione rappresenta il punto in cui il sistema è vincolato.

 Si indica con “ l ”  la lunghezza del pendolo, ossia la distanza tra “O” e il centro di massa.

Un simile sistema impedisce al grave vincolato la caduta verso il basso, consentendogli però di oscillare. Per oscillazione andiamo ad intendere il movimento compiuto da "m" nello spostarsi, partendo con V₀ = 0, dal punto B al punto G e nel ritornare nuovamente nella posizione di partenza  passando così  due volte per il punto di equilibrio A, dove per punto di equilibrio si intende la posizione che il grave assume da fermo. 

Un pendolo oscillante tende a fermarsi se non vi sono altre forze oltre a quella gravitazionale ad “alimentare” il suo movimento. Questo fenomeno, chiamato smorzamento, è solitamente dovuto alla presenza dell’attrito dell’aria.

---

Your browser can't run 1.0 Java applets,so here's a picture of the window the program brings up:  

----------------------->Istruzioni<------------------------

Procediamo analizzando le forze agenti sulla massa m.

Quando m sarà nella posizione di equilibrio A il suo peso
P= m∙g   sarà compensato dalla tensione T del filo.

Supponiamo ora  di lavorare in assenza di ogni tipo di attrito e  spostiamo la massa m da A a B in modo tale che l’angolo θ formato dal filo teso con la verticale sia minore di 6° e lasciamo libera la massa m. Questa si riporterà nella posizione iniziale A di equilibrio sotto l’azione di una forza di richiamo. Il diagramma delle forze agenti su m cambia: il sistema filo-massa non è più in una posizione perpendicolare alla superficie terrestre. L'accelerazione gravitazionale g però lo è tuttora quindi  per giungere alla forza che è causa del movimento dobbiamo scomporre m∙g.  Se assumiamo perciò un asse x tangente all'arco AB di circonferenza e perpendicolare ad  l  disegniamo la componente F_t su tale asse e  la componente P_l lungo la retta  di  l. Cerchiamo ora di trarre delle conclusioni: P_l è evidentemente equilibrata da T  a rimanere ineguagliata è F_t in direzione tangente all’arco che sarà pertanto causa del movimento. Scriviamo quindi la seconda legge della dinamica proiettata sull'asse
F_t = m∙a dove con a intendiamo, come ormai noto, la componente di g su x. 

Essendo l’angolo θ molto piccolo possiamo considerare l’arco AB  uguale al segmento AB e quindi approssimiamo il settore circolare AOB  a un triangolo rettangolo in B che risulterà simile al triangolo rettangolo CDB; quanto detto ci consente di scrivere il seguente rapporto: 

      BD : BC = BA : BO    che tradotto in  termini fisici non sarebbe altro che           F_t :  m∙g = s : l    ossia

   sappiamo inoltre che   

                                                                  (dove T rappresenta chiaramente il periodo)

        quindi  sostituendo 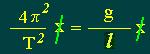          giungiamo concludendo a

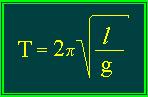
Il moto di un pendolo semplice, nell’ipotesi di piccole oscillazioni, è dunque un moto armonico il cui periodo è del tutto indipendente dalla massa oscillante e dall’ampiezza delle oscillazioni; in altre parole, in una situazione ideale in cui ogni attrito è assente, tutte le oscillazioni di un pendolo semplice hanno la stessa durata (legge dell’isocronismo delle piccole oscillazioni di Galileo)

         -| Credits |-