Sistemi di Riferimento Inerziali

È intuitivo, e la nostra esperienza quotidiana ce  lo conferma, che la velocità di un oggetto può apparire (e talvolta essere) diversa a seconda delle condizioni di moto dell’osservatore. Basti pensare per esempio al moto dei pianeti: tutti sanno che è la Terra a ruotare attorno al Sole, ma per noi osservatori terrestri e facile concludere il contrario se ci  limitamo a osservare la traiettoria del Sole nel cielo (è del resto ciò che si è sempre creduto fino alla rivoluzione copernicana); questo perché noi stessi stiamo in moto nello spazio insieme alla Terra.

È allora opportuno, tutte le volte che si parla di velocità di un oggetto, riferire tale velocità a un sistema di riferimento che sia fermo o perlomeno  in moto lentissimo nello spazio. Un riferimento di questo tipo viene detto assoluto e la velocità di un oggetto misurata da un osservatore solidale con tale sistema viene detta velocità assoluta. Solitamente si assume come riferimento assoluto un sistema di assi cartesiani ortogonale solidale con le stelle fisse, un gruppo di stelle che sono talmente lontane dalla Terra che, anche se soggette a piccoli moti, possono con buona approssimazione essere considerate ferme. Un qualunque altro sistema di riferimento in moto rispetto a quello assoluto viene detto relativo e la velocità di un oggetto misurata da un osservatore solidale con tale sistema viene detta velocità relativa. La relazione tra la velocità assoluta e quella relativa si può ricavare dalla figura 1 , nella quale un oggetto P si trova in un generico istante nella posizione r rispetto al sistema di riferimento assoluto di origine O e nella posizione s rispetto al riferimento relativo di origine o; se la terna in moto occupa nello stesso istante la posizione o rispetto a quella fissa, dalla composizione dei vettori si ha: 
                                      
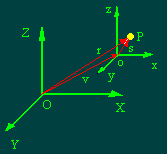  Figura 1

Se ora analizziamo la situazione dopo un tempo Δt la (1) diventa  

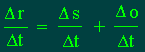
Ovvero chiamando v_a  = Δr/Δt la velocità assoluta del punto P,
v_r = Δs/Δt la sua velocità relativa e v_t = Δo/Δt la velocità di trascinamento con cui la terna mobile si muove rispetto a quella fissa, si ha:

                            v_a = v_r + v_t                                           (2)

Quando si verifica questa relazione il sistema di riferimento relativo viene detto inerziale ossia è un sistema di riferimento che non descrive un moto accelerato.  

Sistemi di Riferimento non Inerziali

Quando invece le varie velocità differiscono per singoli intervalli di tempo allora la (2) diventa

                     
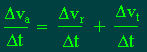
e quindi                a_a = a_r + a_t              

dove a_a è l’accelerazione assoluta, cioè l’accelerazione attribuita all’oggetto in moto dall’osservatore assoluto; a_r è l’accelerazione relativa, cioè l’accelerazione attribuita allo stesso oggetto dall’osservatore relativo; a_t è l’accelerazione di trascinamento, ovvero l’accelerazione che verrebbe attribuita all’oggetto in moto dall’osservatore assoluto  se tale oggetto fosse rigidamente collegato alla terna mobile (si noti che in generale l’accelerazione di trascinamento non è l’accelerazione della terna mobile rispetto a quella fissa).

Queste accelerazioni intervengono in  tre tipi di moto: rotatorio, traslatorio o rototraslatorio. Quando in un sistema di riferimento relativo è sottoposto ad almeno una di tali accelerazioni,  si tratta di un sistema di riferimento non inerziale.

  Forze apparenti

Nell'analisi di sistemi di riferimento relativi non inerziali rientra una particolare categoria di forze  dette forze apparenti. Introduciamo questo tipo di forze con un esempio.

È a tutti noto che, quando un’automobile frena, gli oggetti posti sui sedili tendono a cadere in avanti. L’autista solidale con l’automobile, nell’esaminare il moto dell’oggetto nel proprio sistema O’ (sistema di riferimento relativo solidale con l’automobile), decelerato rispetto a O (sistema di riferimento assoluto solidale con la Terra) , si trova subito in imbarazzo se vuole rendersi conto dell’accaduto alla luce dei principi della dinamica.

Sull’oggetto, posto sul sedile, agiscono infatti il proprio peso e la reazione del sedile che fa equilibrio al peso, per cui l’oggetto dovrebbe restare fermo: questo invece non avviene durante la frenata.

All’inizio della frenata l’oggetto rispetto alla Terra conserva la velocità che aveva l’automobile prima che iniziasse a frenare, rispettando il principio d’inerzia.

Possiamo perciò concludere che le leggi della dinamica valide nel sistema inerziale O non lo sono più nel sistema accelerato o.

Però l’autista può spiegare l’accelerazione dell’oggetto in avanti attribuendola a una “particolare” forza capace di produrla: il tutto viene così inquadrato nella logica della dinamica newtoniana.

Questa forza è detta forza d’inerzia (in quanto come dimostrato prima serve per dare nuovamente validità al principio d’inerzia), forza apparente o forza fittizia.

Dalla discussione fatta emerge che la forza apparente si manifesta nel sistema s in moto accelerato rispetto al sistema inerziale S.

Il risultato può essere generalizzato affermando che le forze apparenti si manifestano nei sistemi o in moto accelerato rispetto a un sistema inerziale.

Nel concludere potremmo intuitivamente affermare che una  una forza reale scaturisce  dall'azione di  un corpo che agisce su un altro corpo, mentre una forza apparente è generata dall'esistenza di un moto accelerato che che coinvolge il sistema di riferimento relativo.

Focalizziamo la nostra attenzione sui sistemi relativi non  inerziali  prendendo  come modello relativo una terna  di assi che si muova di moto  rototraslatorio rispetto ad una assoluta.

Per poter descrivere tale moto un osservatore  solidale alla terna relativa dovrà necessariamente introdurre un particolare tipo di accelerazione nota come  Accelerazione di Coriolis e definita come il prodotto vettoriale      
 dove è definito come  il vettore velocità angolare che ha per modulo  il rapporto Dq (angolo spazzato)/Dt  misurato in rad/s, come direzione l’asse di rotazione del sistema e verso  determinato con il metodo della mano destra.
Il modulo di tale accelerazione sarà quindi     a_c = 2w V_p sen a ,
dove con a intendiamo l’angolo tra i vettori w e V_r .
Aggiungendo questo termine complementare a   e modificando otteniamo allora:     
 meglio noto come teorema delle accelerazioni relative o teorema di Coriolis. Considerando poi la massa del punto materiale andiamo a moltiplicare ottenendo:   
che possiamo riscrivere come   
 analizzando i termini ci accorgiamo che in realtà che solo la F_A è una forza reale perché rappresenta l’effettiva azione fisica che fa accelerare il corpo; la forza esiste solo perché il sistema è in moto rispetto a quello fisso, mentre la (forza di Coriolis) esiste solo perché la terna mobile ruota con velocità angolare rispetto al sistema fisso.

Pertanto la è definita una forza apparente perché introdotta come termine complementare dall’osservatore relativo per giustificare il moto del corpo nella sua terna di riferimento. 

Contrariamente alle aspettative la è molto importante per spiegare fenomeni e comportamenti di corpi sulla Terra.

Non bisogna infatti perdere di vista che la Terra non costituisce un sistema di riferimento, inerziale in quanto ruota intorno al proprio asse e allo stesso tempo descrive un’orbita ellittica intorno al Sole.

Pertanto  focalizzando la nostra attenzione su un corpo di massa m che si muova in un eventuale sistema di riferimento solidale con il pianeta, scriveremo in questo modo il teorema di Coriolis:

                          ma_r =F_A-mw_T²R-2mw_TV_R sen a

dove:   -mw_T²R = F_T   forza apparente di trascinamento  dovuta alla rotazione terrestre, negativa perché forza centripeta;
 w_T=7.29 * 10^-5 rad/s; ed R= raggio vettore.

Il fatto che la Tessa sia un corpo in rotazione è stato dimostrato in diversi modi proprio sfruttando la forza apparente di Coriolis.

  -| Curiosità |-           -| Credits |-