Usare Linux per l'elaborazione di dati numerici

I motivi che mi hanno spinto a rendere disponibile questo manuale sono principalmente due.

Lo scopo del corso di Metodi Numerici era la realizzazione una libreria di routine matematiche e la scrittura del relativo manuale.

Le routine sono state scritte in fortran, sono stati implementati algoritmi per:

  1. calcolo della precisione della macchina (con analisi degli errori)
  2. risoluzioni di sistemi lineari (matrici piene, matrici sparse strutturate e non strutturate)
  3. fitting di dati (interpolazione e smooting, calcolo della spline, polinomi di minimi quadrati)
  4. calcolo della fft
  5. risoluzione di equazioni differenziali
  6. equazioni non lineari (calcolo dello zero di una funzione)
  7. risoluzione di integrali.

Avendo testato tutte le routine sia in Windows che in Linux per verificarne la portabilità ho riscontrato una cattiva gestione da parte di Windows (o delle sue librerie matematiche), di alcune situazioni critiche, mentre in Linux gli stessi problemi sono stati gestiti in modo più appropriato ed utile dal punto di vista dell'utente.

Nella versione html del manuale non ho riportato nessuno dei casi di prova (i test) che ho effettuato per verificare la correttezza delle elaborazioni delle mie routine. I casi di prova, si trovano, comunque, nella versione doc. Riporto qui uno scorcio di una tabella contenente i calcoli effettuati per la ricerca dello zero di una funzione.

Ho implementato due routine per calcolare lo zero di una funzione, in modo da avere una stima della bontà dei risultati ottenuti (a loro volta, confrontati con i valori calcolati da matlab e/o octave sugli stessi valori)

Le routine per il calcolo dello zero di una funzione sono fzero e sec. La prima implementa l'algoritmo di Dekker-Brent, il secondo il metodo delle secanti. Con entrambi ho cercato lo zero della seguente funzione: f=(100/x**2)*sin(10/x).

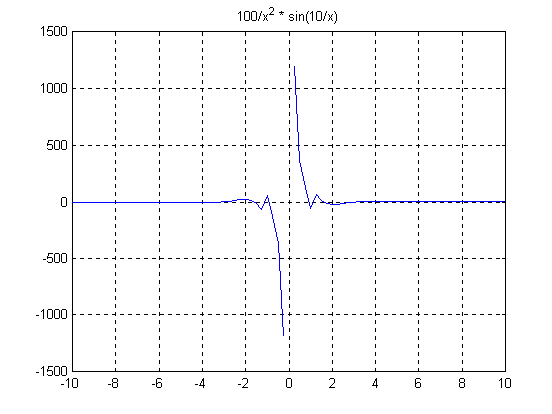
Come potete osservare, la funzione presenta alcune oscillazioni attorno all'origine, inoltre per x->0- f->-infinito, mentre per x->0+ f->+infinito.

La tabella in basso contiene i risultati delle elaborazioni.

Riepilogo dei valori calcolati da sec e fzero sulla funzione f=(100/x**2)*sin(10/x)

Valori calcolati da fzero

Valori calcolati da sec

Stima zero

Val. funzione

Val.

Stima zero

Val. funzione

Val.

Windows

.0000000E+00

.0000000E+00

3

.0000000E+00

.0000000E+00

3

Linux

NAN

NAN

50

NAN

NAN

50

Le due routine eseguite in windows, trovano uno zero in un punto singolare della funzione (l'origine degli assi) e calcolano il valore della funzione nel punto, il tutto effettuando solo 3 eleborazioni.Le stesse routine eseguite in linux, effettuano 50 cicli (il numero massimo consentito dall'utente), e danno come valore dello zero e valore della funzione nel punto NAN (not a number).

I due sistemi operativi, di fronte allo stesso tipo di problema hanno reagito in modo molto diverso. In windows sono stati restituiti dei valori, assurdi, ma assolutamente plausibili per l'utente (a meno che non abbia un'idea dell'andamento della funzione). Mentre in linux, è stata segnalata la situazione anomala, che anche per un utente inesperto può rappresentare un valido aiuto per la ricerca dell'anomalia.

Trovate il Manuale di software matematico qui.

Questo manuale è sottoposto alla licenza Gnu GPL.

Calcolatori Elettronici

Per il corso di Calcolatori elettronici ho realizzato una semplicissima calcolatrice. La macchina preleva, attraverso una tastiera esadecimale, due numeri, un simbolo di operazione matematica, e in seguito ad un segnale di start (tasto uguale "="), la macchina calcola l'operazione richiesta. Il circuito è stato realizzato utilizzando Logic Works.

Copyright © 2001 Nicola Fragale.