Economia...
1.
Gli interessi legali
2. Formule
3. Investimenti
4. Anatocismo: addebito trim. interessi c/c
5. Mutui a tassi usurari?
6.
Trasparenza
7. Il
caso Bipop
8.
Euro 1/1/2002: istruzioni per l'uso
9. Il caso Sanpaolo
IMI
|
|
LE FORMULE DELL'INTERESSE, SCONTO, ECC.
Volete sapere come si calcola l'interesse
o lo sconto? Volete calcolare il tasso di un'operazione
finanziaria? Di seguito trovate un elenco di formule.
Nota: Per quanto ovvio, precisiamo che il simbolo della
moltiplicazione (x) può essere omesso (come negli esempi che
seguono) o sostituito dal puntino (.)
- Interesse semplice e Montante
- L'interesse semplice è
il compenso spettante a chi dà in prestito un capitale, ad un certo tasso,
per un certo tempo (vedi anche interesse
composto). Pertanto
alla scadenza si dovrà restituire il montante,
ossia la somma del capitale + interesse. Nella pratica
commerciale il compenso per l'interesse si indica in forma
percentuale (%); 9% significa che la remunerazione del capitale
è di 9 euro di interesse ogni 100 euro di capitale per un anno. La
misura percentuale con cui si indica l'interesse per un anno si chiama
ragione o saggio o tasso percentuale di interesse
(es.:
interesse del 9% annuo); viene
indicato simbolicamente con r. In matematica
finanziaria viene invece indicato per 1 euro di capitale (es.: interesse
pari a 0,09 euro annui). In questo caso si parla di ragione
o saggio o tasso unitario di interesse; viene
rappresentato con il simbolo i.
-
1.a) Il calcolo dell'interesse semplice
(tempo in anni)
-
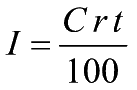
-
- I=Interesse
C=Capitale
iniziale t=tempo
(espresso in anni)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
- Esempio:
- Prendo a prestito un Capitale di € 50.000,00 al 9% per 2 anni.
Quale interesse dovrò pagare alla scadenza?
- I = 50.000,00 x 9 x 2
= 9.000,00 € (interessi
totali da pagare)
-
100
*
E se voglio calcolare il
Capitale o il tasso, partendo dagli altri elementi?
- 1.b) Il calcolo del capitale iniziale
(tempo in anni)
-
-
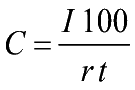
- C=Capitale
iniziale I=Interesse
t=tempo
(espresso in anni)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
-
- Esempio:
- C = 9.000,00 x 100
= 50.000,00 € (capitale
iniziale)
-
9 x 2
-
- *
- 1.c) Il calcolo del tasso
(tempo in anni)
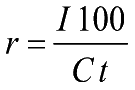
-
- C=Capitale
iniziale I=Interesse
t=tempo
(espresso in anni)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
Esempio:
- r = 9.000,00 x 100
= 9 % (tasso)
- 50.000,00
x 2
-
*
- 1.d) Il calcolo del montante
(tempo in anni)
- Somma di Capitale e Interessi.
-
-
-
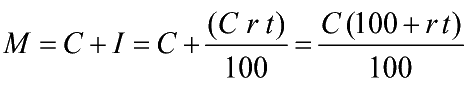
-
-
-
- M=Montante
- C=Capitale
iniziale I=Interesse
t=tempo
(espresso in anni)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
-
Esempio:
- M = 50.000,00 +
50.000,00 x 9 x 2
= 59.000,00 € (montante: capitale+int.)
-
100
Se il tempo è in mesi o giorni,
al Capitale sommare gli Interessi utilizzando le formule indicate ai
punti 1.e) e
1.f),
oppure usare la formula del punto 1.h).
*
E se voglio fare calcoli
basandomi su tempi espressi in mesi e giorni, anziché anni?
- 1.e) Il calcolo dell'interesse semplice (tempo in
mesi)
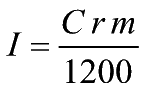 -
-
- I=Interesse
C=Capitale
iniziale m=tempo
(espresso in mesi)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
- Esempio:
- Prendo a prestito un Capitale di € 50.000,00 al 9% per 6 mesi.
Quale interesse dovrò pagare alla scadenza?
-
-
- I = 50.000,00 x 9 x 6
= 2.250,00 € (interessi
totali da pagare)
-
1200
-
- *
-
- 1.f) Il calcolo dell'interesse semplice
(tempo in giorni)
- *ANNO CIVILE* (365 giorni)
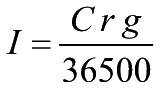 -
- I=Interesse
C=Capitale
iniziale g=tempo
(espresso in giorni)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
- Esempio:
-
-
- Prendo a prestito un Capitale di € 50.000,00 al 9% per 180 giorni.
Quale interesse dovrò pagare alla scadenza?
I = 50.000,00 x 9 x 180
= 2.219,18 € (interessi
totali da pagare)
36500
*
- 1.g) Il calcolo dell'interesse semplice
(tempo in giorni)
- I. *ANNO COMMERCIALE* (360 giorni)
- II. *PROCEDIMENTO MISTO* (anno comm.,; giorni
secondo il calendario civile).
-
- Queste formule vengono utilizzate in
certi calcoli commerciali e bancari. In entrambe si usa l'anno
commerciale di 360 giorni al denominatore della formula (36000); nella
prima (I. *ANNO COMM.*) viene usato anche al numeratore (tutti i mesi vengono
considerati di 30 giorni), mentre nella seconda (II. *PROC. MISTO*)
si usa il calendario
civile di 365 giorni.
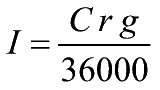 -
- I=Interesse
C=Capitale
iniziale g=tempo
(espresso in giorni)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
- Esempio:
- Prendo a prestito un Capitale di € 50.000,00 al 9% per 180 giorni.
Quale interesse dovrò pagare alla scadenza?
-
-
-
- I = 50.000,00 x 9 x 180
= 2.250,00 € (interessi
totali da pagare)
-
36000
-
-
*
- 1.h) Il calcolo del montante (tempo in
giorni)
- Somma di Capitale e Interessi.
*ANNO CIVILE* (365 giorni)
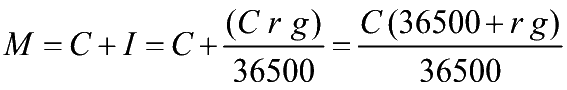
- M=Montante
- C=Capitale
iniziale I=Interesse
g=tempo
(espresso in giorni)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
Esempio:
- M = 50.000,00 +
50.000,00 x 9 x 180
= 52.219,18 € (montante: capitale+int.)
-
36500
*
- Sconto e valore attuale
- Lo sconto non è
altro che l'interesse che deve essere detratto dal capitale, anziché
sommarlo. Il valore attuale è
dato dalla differenza tra capitale e sconto.
-
- 2.a) Il calcolo dello sconto mercantile
- E' lo sconto "secco",
senza tenere conto del tempo; viene di solito utilizzato nel commercio
al dettaglio (negozi).
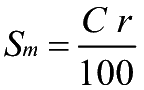 -
-
- Sm=Sconto
mercantile C=Capitale
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
- Esempio:
- Acquisto un vestito in un negozio che costa € 50,00 e riesco ad
ottenere uno sconto del 10%. Qual è lo sconto?
- Sm = 50,00 x
10
= 5,00 € (sconto
mercantile)
-
100
Naturalmente per sapere quanto dovrò pagare devo detrarre lo sconto
dal capitale:
50,00 - 5,00 = 45,00 €
*
- 2.b) Il calcolo dello sconto commerciale
(tempo in
giorni)
- *ANNO CIVILE* (365 giorni)
- E' lo sconto per eccellenza, che viene calcolato
come l'interesse, ossia tenendo conto del tempo; deve essere detratto
dal capitale, anziché essere sommato. Di solito rappresenta il
compenso spettante a chi paga un debito prima della scadenza,
calcolato in proporzione al capitale da pagare a scadenza, al tasso e
al tempo di anticipo.
- Viene normalmente applicato in ambito
commerciale per brevi periodi. In effetti la
formula è finanziariamente inesatta
e se applicata su lunghi periodi dà luogo a risultati assurdi.
Questo accade perché nella formula dello sconto commerciale si
applica la formula dell'interesse (giustamente), ma non si utilizzano
gli stessi parametri, in particolare il Capitale: infatti per un
calcolo esatto bisognerebbe
utilizzare il Capitale iniziale
(nello sconto si chiama Valore attuale), mentre
nello sconto conosciamo solo il Capitale finale.
Se vogliamo effettuare un calcolo esatto basandoci sul Capitale
iniziale, anche se non lo conosciamo, dobbiamo utilizzare la formula
dello Sconto razionale.
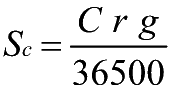 -
-
- Sc=Sconto
commerciale g=tempo
(espresso in giorni)
- C=Capitale
a scadenza (o valore nominale o capitale nominale)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
- Esempio:
-
-
- Ho contratto un debito pari a € 50.000,00. Se pago in anticipo
rispetto alla scadenza concordata, il creditore mi riconosce uno sconto
del 9% su base annua. Pago con 10 giorni di anticipo. Quale sconto avrò
al momento in cui rimborserò il debito?
Sc = 50.000,00 x 9 x
10
= 123,29 € (sconto
commerciale)
36500
*
- 2.c) Il calcolo del valore attuale
commerciale (tempo in
giorni)
- Differenza tra Capitale e Sconto
commerciale *ANNO CIVILE* (365 giorni)
-
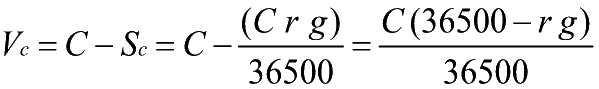
-
- Vc=Valore
attuale commerciale (Capitale iniziale)
- Sc=Sconto
commerciale g=tempo
(espresso in giorni)
- C=Capitale
a scadenza (o valore nominale o capitale nominale)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
- Esempio:
- Vc = 50.000,00 - 50.000,00 x 9
x 10 = 49.876,71
€ (val.att.: cap.-int.)
-
36500
*
- 2.d) Il calcolo dello sconto razionale (tempo in
giorni)
- *ANNO CIVILE* (365 giorni)
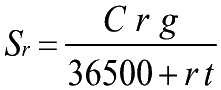 -
- Sr=Sconto
razionale g=tempo
(espresso in giorni)
- C=Capitale
a scadenza (o valore nominale o capitale nominale)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
- Esempio:
Sc = 50.000,00 x 9 x
10
= 122,98 (sconto
razionale
36500
+ (9 x 10)
*
- 2.e) Il calcolo del valore attuale
razionale (tempo in
giorni)
- Differenza tra Capitale e Sconto
razionale *ANNO CIVILE* (365 giorni)
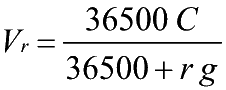 -
- Vr=Valore
attuale razionale (Capitale iniziale)
- g=tempo
(espresso in giorni)
- C=Capitale
a scadenza (o valore nominale o capitale nominale)
- r=ragione
o saggio o tasso percentuale (%) di interesse
-
-
- Esempio:
-
-
-
- V =
36500 x 50.000,00
= 49.877,02 € (valore attuale
razionale)
-
36500 + (9 x 10)
-
-
-
-
-
-
*
-
-
-
-
-
-
-
-
-
- Interesse e Sconto composto
-
- L'interesse composto
è simile all'interesse semplice, ma si applica quando questo viene
"capitalizzato", normalmente almeno ogni anno. Infatti in alcuni casi, come per i
c/c bancari, l'interesse viene periodicamente sommato al capitale
iniziale (solitamente ogni trimestre le banche accreditano/addebitano l'interesse
sul c/c). La capitalizzazione è l'interesse che diviene a sua
volta capitale e produce anch'esso altri interessi. La formula
dell'interesse semplice invece non prevede la capitalizzazione:
è necessaria una formula diversa che tenga conto dell'interesse che
diventa capitale. Di seguito mostriamo come si calcola
l'interesse composto e il suo montante.
- 3.a) Il calcolo del montante ad
interesse composto
- Somma di Capitale e Interessi in caso di
una o più capitalizzazioni
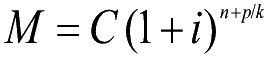
- M=Montante
- C=Capitale
iniziale
- n=tempo
unitario (n.° di capitalizzazioni)
- p/k=tempo
frazionato (tempo residuo inferiore al periodo di capitalizzaz.)
- i=tasso unitario di interesse del periodo (es.°:
9% = 0,09)
- Esempio:
Ho
un capitale di € 50.000,00 depositato su un c/c bancario che mi frutta
il 2%. La capitalizzazione è trimestrale (ogni 3 mesi mi accreditano
gli interessi). Che capitale avrò sul conto fra 1 anno e 2 mesi (14
mesi)? Per praticità non consideriamo né spese e commissioni bancarie,
né bolli e ritenuta fiscale da pagare allo Stato.
Periodo
complessivo: 14 mesi.
In un anno (12
mesi) ci sono 4 capitalizzazioni trimestrali (n=4).
I rimanenti 2
mesi sono pari ai 2/3 di un trimestre, cioè del periodo di
capitalizzazione (p/k=2/3).
Siccome le
capitalizzazioni sono trimestrali dobbiamo trasformare il tasso annuo in
tasso trimestrale. Il tasso percentuale annuo del 2% è pari allo 0,02
unitario annuo (2:100=0,02); (0,02:4=0,005) quindi il tasso unitario
trimestrale è lo 0,005 (i=0,005).
M = 50.000,00 x
(1 + 0,005)4+2/3 = 50.375,47
€
-
(montante ad interesse composto)
*
3.b)
Il calcolo del valore attuale ad interesse composto
Differenza tra Capitale e Interessi in caso di una o più
capitalizzazioni.
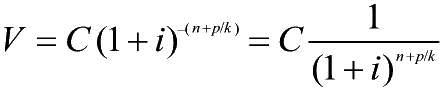
-
- V=Valore
attuale con lo sconto composto
- C=Capitale
finale
- n=tempo
unitario (n.° di capitalizzazioni)
- p/k=tempo
frazionato (tempo residuo inferiore al periodo di capitalizzazione)
- i=tasso unitario di interesse del periodo (es.°:
9% = 0,09)
Se
la capitalizzazione avviene ogni trimestre e il periodo è di 14 mesi,
allora le capitalizzazioni sono quattro: n=4;
(4x3=12 mesi) più altri due mesi: p/k=2/3
(2 mesi su tre del trimestre).
Esempio:
1
V
= 50.000,00 x _______________ = 49.624,53
€ (val.attuale composto)
(1 + 0,005)4+2/3
*
|
![]()