1. Scegliere una nuova formula
2. Usare lo switching
3. Zoomare su un particolare dell'immagine
4. Scegliere un algoritmo di colorazione
5. Usare l'editor del gradiente
6. Aggiungere dei layer all'immagine.

Alla fine otterremo l'immagine a destra: è un esempio di come, con poche e semplici operazioni, si possa ottenere un'immagine non banale. E adesso cominciamo.

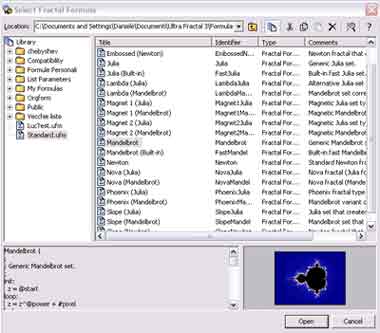
1) Scegliere una nuova Formula

Come prima cosa, dovete aprire il programma :-)

Fatto questo, chuedete l'immagine di mandelbrot che appare per default (se non avete cambiato le impostazioni dalle opzioni); vogliamo partire completamente da 0. A questo punto, cliccate, nella toolbar, il pulsante New Fractal , oppure premete la combinazione CTRL+N, e comparirà la finestra che appare a destra; questa finestra vi permette di navigare fra le formule del vostro database: la cartella più importante è quella Public, dove risiedono le formule del database pubblico, ma potete anche creare altre cartelle dove mettere le vostre formule, e organizzarle come meglio credete.

Nella sinistra, c'è l'albero delle formule, contenente le cartelle e i files: a destra, c'è la lista delle formule presente in un determinato file che avete scelto nell'albero. Sotto, appaiono sia una piccola immagine rappresentante il frattale (con i parametri predefiniti), e il listato della formula. Adesso, per procedere, scegliete il file Standard.ufm, ed aprite la formula Mandelbrot, cliccandoci sopra e premendo Open (o facendo doppio clic).

A questo punto apparirà l'immagine a destra, che rappresenta il frattale di Mandelbrot, che conoscete bene: tuttavia, non voglio usare il frattale di Mandelbrot per creare l'immagine, ma un frattale di Julia. Allora perchè ho aperto il frattale di Mandelbrot?

Per il semplice fatto che lo useremo per scegliere il nostro frattale di Julia: sappiamo dalla teoria che ad ogni punto del piano complesso rappresentante il frattale di Mandelbrot corrisponde un determinato frattale di Julia: adesso, medianto lo switching, possiamo passare da una formula all'altra. Vediamo come.

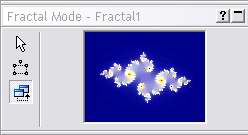
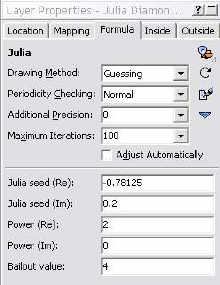
2) Usare lo switching

Cercate nella toolbar il pulsante Switch Mode (che potete trovare anche nella finestra Fractal Mode, oppure potete premere F7). A questo punto, potete notare che nella finestra Fractal Mode appare una piccola finestrella, che rappresenta un frattale di Julia: se, adesso, muovete il cursore del mouse lungo l'immagine del frattale di Mandelbrot, vedrete cambiare l'immagine: in pratica, l'immagine nella finestra Fractal Mode rappresenta il frattale di Julia corrispondente al punto dove si trova il cursore del mouse.

Divertitevi a vedere come varia questa immagine mentre vi muovete nel frattale di Mandelbrot: poi scegliete un punto che crei l'immagine a destra (a voi il piacere di scoprire dove si trovi questa zona); fate clic col mouse, e si aprirà una nuova finestra, a grandezza normale, col frattale di Julia che avete scelto: per creare una immagine esattamente come la mia, dopo lo switch, potete regolare il seme dell'insieme di Julia (il parametro Julia Seed nella cartella formula del Layer Properties), inserendo questo valore (potete copiarlo ed incollarlo):

A questo punto avrete l'immagine a destra, che rappresenta l'insieme di Julia: ci interessa adesso ingrandirne un particolare, in particolare voglio lavorare su una delle sue spirali: per farlo, ho bisogno di zoomare su una delle spirali.

3) Zoomare

La zona in particolare su cui voglio zoomare è rappresentata da una delle due spirali centrali: prendiamone una, diciamo quella a destra.

Clicchiamo sul centro della spirale, e tenendo premuto il pulsante (sinistro, ma lo capite da soli) del mouse, trasciniamo il rettangolo di selezione: notate, mentre lo trascinate, un paio di cosette: prima di tutto, rimane sempre delle stesse proporzioni della finestra principale (per evitare distorsioni, che potete effettuare comunque variano di valori di Stretch e Skew nella cartella Location del Layer Properties); come seconda cosa, notate sempre nella finestra del Fractal Mode il particolare della zona ingrandita.

A questo punto, cliccando col pulsante sinistro del mouse, verrà ingrandita l'immagine, portando la spirale ad occupare tutta la finestra: niente vi vieta di sperimentare: provate ora a vedere la caratteristica di autosomiglianza dei frattali, provando ad ingrandire sempre di più particoarli via via più fini. Se, facendolo, notate delle zone nere dovute all'approssimazione per il basso numero d'iterazioni, aumentatele nella cartella formula del Layer Properties.

Dopo che vi siete divertiti, per ottenere l'immagine a destra usate le seguenti impostazioni, che potete mettere nella Location Tab del Layer Properties:

• Center: 0.51875/-0.09375
• Magnification: 8.5714286

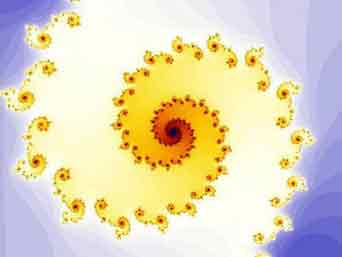
Otterrete l'immagine a destra: adesso si tratta di elaborarla, scegliendo un algoritmo di colorazione che renda l'immagine più interessante (anche se è già bella così, non trovate?).