|
I numeri Complessi
Vedremo adesso come si fa a creare il frattale di Mandelbrot. Prima di procedere, però, è opportuno fare un piccolo ripasso sui numeri complessi (se conosci l'argomento, potete anche saltare l'argomento, ed andare direttamente alla pagina successiva).
Do per scontato che sai fare la radice quadrata i un numero normale, vero? Sai che  , e sai anche che , e sai anche che  : quasi sicuramente saprai anche che la radice quadrata di un numero negativo non si può fare, a meno di no introdurre un nuovo ente matematico: l'unita immaginaria i (oppure j a seconda di testi e libri vari: la sostanza non cambia). : quasi sicuramente saprai anche che la radice quadrata di un numero negativo non si può fare, a meno di no introdurre un nuovo ente matematico: l'unita immaginaria i (oppure j a seconda di testi e libri vari: la sostanza non cambia).
Questa entità è definita come la radice dell'unità negativa, ossia ho  . In questo modo posso fare la radice negativa di numeri negativi, considerandoli come prodotto di un numero positivo per -1, e usando le proprietà della radice quadrata; in questo modo ho . In questo modo posso fare la radice negativa di numeri negativi, considerandoli come prodotto di un numero positivo per -1, e usando le proprietà della radice quadrata; in questo modo ho 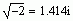 , che rappresenta un numero immaginario. , che rappresenta un numero immaginario.
I numeri complessi, allora, sono considerati come enti matematici formati da una parte reale ed una parte immaginaria: ad esempio 6-4i è un numero complesso.
Le semplici operazioni si fanno esattamente come per i polinomi, considerando separate la parte reale e la parte immaginaria. Per esempio ho:
(4+3i)+(-2-8i) = (4-2)+(3-8)i = 2-5i
5*(2+6i) = (5*2)+(5*6)i = 10+30i
(3+4i)*(2+5i) = (3+2)+(3*5)i+(4*2)i+(4*5)i2 = -14+23i
Questo ultimo risultato è stato ottenuto considerando che, conseguente alla definizione dell'ente immaginario i, i2 = -1.
Per operazioni più complicate, come seni, coseni etc, vari studiosi li hanno analizzati, e definiti anche per numeri complessi, attraverso varie proprietà matematiche: così, ad esempio, avremo:
Non posso dire come si ci arriva, sopratutto perchè non è di questo che dobbiamo parlare, ma anche perchè non è chiarissimo neanche a me :-).
Possiamo rappresentare graficamente questi numeri complessi: dato che la parte reale ed immaginaria sono distinte, possiamo pensare di disegnare un grafico cartesiano, dove l'asse delle ascisse rappresenta la parte reale del numero complesso, e l'asse delle ordinate rappresenti la parte immaginaria; in questo piano, chiamato piano di Gauss, ogni numero complesso sarà rappresentato da un punto, aventi come coordinate i suoi valori.
|

![]()

![]()