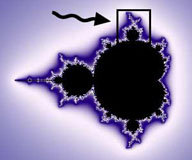
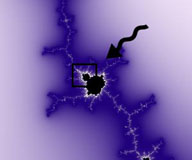
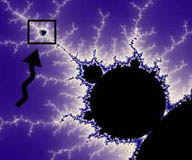
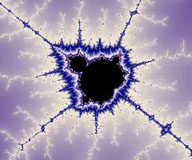
I frattali, invece, hanno la particolarità che hanno un numero di dettagli infinito: ingrandendo sempre di più una immagine frattale scopriamo sempre nuovi particolari, nuove forme prima invisibili soltanto perchè troppo piccole, e così via all'infinito. In molti frattali, poi, questi particolari che si vanno man mano scoprendo assomigliano alla figura nella sua totalità: da questo il termine autosomiglianza.

Nelle figure a destra possiamo vedere un esempio di autosomiglianza nel più classico e famoso frattale : il frattale di Mandelbrot (dal nome del suo scopritore).

Queste figure sono generate, per la maggior parte dei casi, mediante l'applicazione di formule iterative nel piano dei numeri complessi: numeri aventi, cioè, una parte reale e una immaginaria. L'unità immaginaria è definita come la radice quadrati di -1: vedremo meglio nella teoria di base come funzionano le cose.

Di frattali ce ne sono di un'infinità di tipi. Ormai sono utilizzati nella maggior parte della scienza moderna, che sfrutta e usa proprietà matematiche che, per la loro difficoltà o per la loro recente scoperta, non sono state utilizzate precedentemente, come, per esempio, le teorie sulla risoluzione di sistemi non lineari, complicati dal punto di vista teorico, tanto quanto da quello pratico: oppure nella creazione dei transistor e diodi di dimensioni microscopiche, i quali processi ormai non è più possibile calcolarli con la matematica ordinaria.

Nonostante questi tipi di frattali siano molto comuni ed importanti, non sono gli unici: ne esistono di altri tipi: per esempio i frattali iterativi, gli L-System, oppure ancora i quaternioni. Sono frattali ottenuti con regole matematiche diverse: per esempio, i frattali L-System si ottengono applicando delle regole iterative. Con semplicissimi regole gli studiosi sono in grado di riprodurre comportamenti anche complessi, come il movimento delle folle, oppure ancora la crescita di una pianta. Da delle semplici regole si possono ottenere risultati totalmente inaspettati ed interessanti.

Vedremo più avanti come si possono creare questi tipi di frattali