Switching

Lo switching rappresenta il metodo per passare da un punto dell'insieme di Mandelbrot al corrispondente insieme di Julia.

Abbiamo visto poco fa che gli insiemi di Mandelbrot e Julia sono stati creati a partire dalla medesima formula: la differenza consisteva nei valori iniziali delle costanto z₀ e c. La c della iterazione dell'insieme di Julia rimane costante mentre disegnamo l'insieme, ed è lecito immaginare che al variare della c (che abbiamo chiamato seme), vari l'insieme di Julia. Questo è normale, dato che è l'unica variabile personalizzabile dell'iterazione.

Supponiamo, adesso, di avere l'insieme di Mandelbrot. Prendiamo un punto di questo insieme, e usaiamolo come seme per l'insieme di Julia: in questomodo si vede come spunti una relazione (biunivoca) fra punti del piano complesso in cui rappresentiamo l'insieme di Mandelbrot, e la totalità degli insiemi di Julia, che variano al variare di c.

Prendiamo, quindi, vari punti, e vediamo il corrispondente insieme di Julia. Possiamo vedere come l'insieme di Julia vari molto a seconda del seme iniziale. si può notare subito una proprietà importante: insiemi di Julia con seme interno all'insieme di Mandelbrot, hanno anch'essi una parte interna. Punti che hanno come seme un punto esterno all'insieme di Mandelbrot, sono privi di parte interna (si dice che sono a misura nulla).

Anche la forma che assumono dipende da dove prendiamo il punto: per esempio, il punto A genera un insieme di Julia abbastanza semplice, mentre il punto B, che è sempre interno all'insieme, è già più ricco di partocolari, perchè l'abbiamo preso in un cerchio secondario.

Per gli insiemi ottenuti da punti esterni, invece, possiamo vedere che, in generale, la loro ricchezza di particolari diminuisce all'aumentare della distanza dall'insieme di Mandelbrot.

In genere, si è visto che c'è una profonda connessione fra proprietà di un punto dell'insieme di Mandelbrot, e proprietà del corrispettivo insieme di Julia (periodi di orbita e pre-orbita, ramificazione etc) che porta ad una profonda teoria. Sono relazioni abbastanza complesse per parlarne qui, ma si può vederne qualcuna anche esteticamente. Per esempio, notate come l'insieme di Julia C rispetti la forma dell'insime di mandelbrot nella zona dove viene preso, chiamata in genere zona del cavalluccio marino.

La regolarità negli insiemi di Mandelbrot si ripetono nei corrispettivi insiemi di Julia. Ad esempio, se prendiamo un punto dell'insieme di Mandelbrot, all'interno di un cardioide più piccolo, vedremo un insieme di Julia corrispondente che contiene piccole copie del'inisme di Julia corrispondente al cardioide principale per quel medesimo punto. La varietà è praticamente infinita.

Ci sono anche alcune differenze degli insiemi di Julia rispetto all'inisme di Mandelbrot: Gli insiemi di Julia sono, per così dire, molto più autosimili dell'insieme di Mandelbrot.

Per esempio, ingrandendo molto l'insieme di Mandelbrot, saremo in grado di scovarne un altropiù piccolo, ma circondato da una mriade di dendriti e piccole spirale che lo cirondando e si connettono ad esso. Siamo in grado di distinguere perfettamente l'insieme di Mandelbrot più piccolo dal quello principale.

Al contrario, gli insiemi di Julia hanno una autosimiliarità molto più spinta, e, a parte quando lo guardiamo nella loro totalità, se ne visualizziamo un partiolare non siamo in grado di distinguere se appartiene, per così dire, alla figura principale, oppure ad una sua copia, perchè non è circondato da dendriti e affini, che permettano di distinguere la zona in cui ci troviamo.

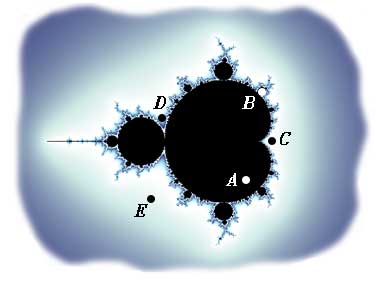
Insieme di Mandelbrot con evidenziati i punti presi come semi degli insiemi di Julia sottostanti.