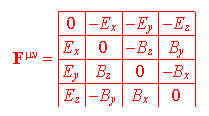
Lezione 21

*Le equazioni di Maxwell*

di Michele Moroni

Versione 3.1 gennaio 2005

Nella lezione 19 abbiamo definito il tensore elettromagnetico come

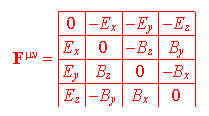
mentre nella lezione 20 abbiano dimostrato che sono le quattro componenti di un quadrivettore K
[dato che il simbolo B è già presente nel tensore elettromagnetico abbiamo sostituito B con K per evitare confusione, ]

Esplicitando quest'ultima relazione nelle corrispondenti 4 equazioni si ottiene:

,

,

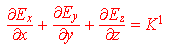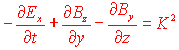
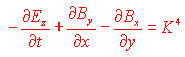
La prima di queste equazioni può essere riscritta come

(1)

( il vettore nabla tridimensionale, componente spaziale di quello quadridimensionale)

mentre sommando le altre 3 e indicando con la componente spaziale di K, queste possono essere riscritte vettorialmente(2)

Ma nella lezione C1 abbiamo dimostrato che

(3)

(Prima equazione di Maxwell)

confrontando la (3) con la (1) è quindi evidente che la componente temporale del vettore K è

Sappiamo inoltre dalla lezione 12a che la densità di carica elettrica r forma con la densità di corrente j un quadrivettore J [quadrivettore densità di corrente]. Risulta quindi ovvio che deve essere valida la seguente relazione

Per cui, l'equazione (2) può essere scritta come

Quarta equazione di Maxwell

Si può inoltre notare che la prima e la quarta equazione di Maxwell possono essere scritte in maniera elegantissima e semplice

Prima e quarta equazione di Maxwell in forma relativistica

_______________

Consideriamo ora l'espressione del tensore elettromagnetico covariante (si veda lezione 19)

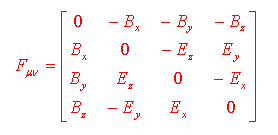
E la sua legge di trasformazione

Ora, sappiamo, dalla lezione 20 che

dove P_v sono le componenti di una unoforma

Ricordando che 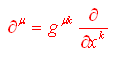ed esplicitando la relazione precedente si ottiene

,

,

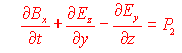
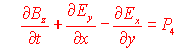
Con procedura analoga a quella svolta nella prima parte possiamo quindi scrivere queste equazioni in forma compatta vettoriale

(7b)

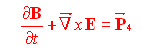(8b)

(dove, come al solito la freccia indica la componente spaziale di un tensore)

Dobbiamo ora calcolare la diverenza di B ...

L'espressione esplicita del campo magnetico da noi ricavato per un filo rettilineo (si veda lezione 12c) è

E quindi B coincide con la sua componente B_f

Ma B_f non è funzione di f e quindi risulta senz'altro

(9b)

(seconda equazione di Maxwell)

Questo risultato è abbondantemente confermato sperimentalmente e attualmente non si conosce eccezione a questa relazione

Per confronto della (7b) con la (9b) risulta evidente che

K₁=0

Ma la cosa più interesante è che essendo , ed essendo I' indipendente da f in ogni sistema di riferimento allora rusulta anche e quindi

la divergenza di B risulta invariante in ogni sistema di riferimento

Conseguentemente P ha componente temporale nulla in qualsiasi sistema di riferimento. L'unica unoforma che soddisfa questa proprietà è l'unoforma nulla e quindi

P = 0

Conseguentemente la relazione (8b) può essere riscritta come

Terza equazione di Maxwell

Ricapitolando possiamo scrivere le equazioni di maxwell come

 

Indice Lezioni - Lezione Precedente - Lezione Seguente