
Lezione 12a
*Relatività e carica elettrica*
Versione 2.0 Marzo 2004
Prendiamo un blocco di materiale condutore inizialmente scarico e portiamolo ad alta temperatura. Ovviamente gli elettroni hanno una massa diversa da quella dei protoni e quindi, in seguito al riscaldamento, la loro velocità cambia in maniera differente. Se la carica di una particella dipendesse dalla sua velocità la carica dei protoni e degli elettroni non si equilibrerebbe più e quindi il corpo si caricherebbe. Dato che nessun fenomeno del genere è mai stato osservato possiamo arrivare alla seguente conclusione:
La carica elettrica apparente di una particella è uno scalare invariante, ovvero non dipende dalla velocità della particella rispetto all'osservatore.
Consideriamo ora un tubo molto lungo (al limite infinitamente lungo) e di base molto piccola dS (al limite infinitesima) al cui interno troviamo delle particelle immobili rispetto ad un osservatore O, distribuite uniformemente con una densità di carica r
Per comodità supponiamo l'asse del tubo disposto lungo l'asse delle x.
Se consideriamo una sezione cilindrica di volume dV=dSl la densità di carica è uguale alla carica totale dq contenuta in dV diviso il volume stesso del cilindro dV

Consideriamo ora un sistema di riferimento O' che si muove lungo l'asse delle x con velocità vd rispetto al sistema di riferimento O (Ciò equivale a dire che le cariche si muovono lungo l'asse delle x con velocità -vd rispetto ad O' ).
La lunghezza l nel sistema O' si contrae di un fattore (si veda lezione 4)
![]()
mentre la superficie di base S, perpendicolare alla direzione di moto, rimane invariata.
Conseguentemente il volume del cilindro risulta variato di un fattore
![]()
Essendo la carica totale interna invariata possiamo senz'altro scrivere l'espressione della densità di carica vista dall'osservatore O'.
 (1)
(1)
In seguito al cambiamento del sistema di riferimento si genera una corrente di carica
![]()
j' è la densità di corrente dato dal prodotto della densità di carica in O' per la velocità di drift (ovviamente è un vettore, dato che vd è una grandezza vettoriale).
n è un versore perpendicolare alla superficie dS e rivolto lungo la direzione positiva dell'asse delle x.
risulta quindi che il vettore densità di corrente in O' è dato da
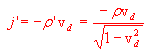
Consideriamo quindi un osservatore esterno O'' che si muove lungo la direzione dell'asse del tubo con velocità v rispetto ad O' (il quale sappiamo che si muove con velocità vd rispetto ad O).La legge di composizione delle velocità (si veda lezione 11) ci permette di calcolare la velocità u di O'' rispetto ad O
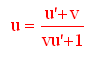
Risulta quindi che la densità di carica vista in O'' è:
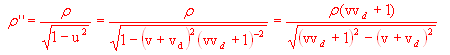
ovvero, semplificando

Calcoliamo ora la densità di corrente nel sistema di riferimento O'':
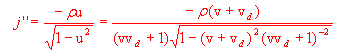
da cui
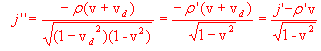
Le precedenti relazioni possono essere scritte in forma matriciale come:
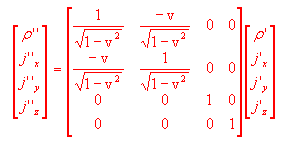
Quindi possiamo affermare che in generale
J = [r, j]
è un quadrivettore, in quanto soddisfa le leggi di trasformazione dei quadrivettori
Questo in generale viene chiamato "QUADRIVETTORE CARICA ELETTRICA"