Lezione 20

*gradiente e tensori*

di Michele Moroni

Consideriamo un tensore di tipo 2/0 di componenti,e uno di tipo 0/1 di componenti. Vogliamo dimostrare che il prodotto definito dalla seguente relazione

(1)

definisce un quadrivettore, e come tale le componenti si trasformano come le componenti di un quadrivettore (giustificando l'indice esponente).

Per dimostrarlo basta considerare le leggi di trasformazione dei tensori 0/1 e 2/0 (lezioni 13 e 14) e vedere come si trasforma quando in un sistema di riferimento in moto con velocità v. Risulta di derivazione immediata la relazione

la quale basta ampiamente a gisutificare l'espressione (1).

In maniera perfettamente analoga possiamo dimostrare che il prodotto

tra un quadrivettore (tensore 1/0) e un tensore di tipo 0/2 definisce una unoforma (tensore 0/1) e quindi è perfettamente giustificato l'indice deponente.

____________

Abbiamo già dimostrato (vedi lezione 17) che è sempre verificata la seguente legge di trasformazione

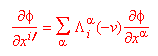
(dove f era un invariante lorenziano). Conseguentemente risulta anche verificata la

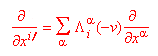
Si può quindi osservare che, indicando con , la precedente relazione si riscrive in

la quale è esattamente la legge di trasformazione dei tensori 0/1.

Risulta quindi giustificato l'indice deponente nella notazione , in quanto queste si trasformano proprio come le componenti di un tensore 0/1.

Con procedura perfettamente analoga possiamo definire le quattro componenti e osservare che si trasformano secondo la relazione

___________

Dalle precedenti considerazioni risulta ovvio che le quattro componenti

sono le componenti di un quadrivettore

mentre le quattro componenti

sono le componenti di una unoforma

Indice Lezioni - Lezione Precedente - Lezione Seguente