Se H è un
trivettore tale che 
allora
esiste un campo scalare Y
tale che 
allora
esiste un campo scalare Y
tale che Lezione 22
*Il potenziale vettore magnetico*
Enunceremo ora due teoremi matematici che non dimostreremo (ciò esula dallo scopo di queste lezioni; chiunque volesse approfondire può sicuramente trovare le dimostrazioni su ogni buon testo di analisi matematica 2).
Teorema 1
|
Se H è un
trivettore tale che
allora
esiste un campo scalare Y
tale che |
Teorema 2
|
Se H è
un trivettore tale che
 allora
esiste un campo vettoriale C tale
che  |
(PS: La freccia sopra il simbolo di vettore è utilizzata per definire la parte spaziale di un quadrivettore)
Consideriamo ora la seconda equazione di Maxwell (vedi lezione 21)
Dal teorema 2 risulta chiaro che esiste un campo vettoriale A tale che in ogni punto dello spazio soddisfa la relazione
(1)
Il vettore A che soddisfa la precedente proprietà è chiamato POTENZIALE VETTORE MAGNETICO
___________
Possiamo notare immediatamente che A
non è univocamente definito. Infatti se Y
è un qualsiasi campo scalare è possibile definire
un vettore 
che , inserito al posto di A nell'equazione
(1), fornisce esattamente lo stesso campo B.
(Infatti si dimostra
banalmente che le tre componenti di 
sono
identicamente nulle).
Consideriamo ora uno specifico potenziale vettore A. Questo sarà ovviamente caratterizzato in ogni punto da un certo rotore e da una certa divergenza. Quale sarà la divergenza di A'? risulta che
Dato che Y
può essere qualsiasi cosa anche la divergenza di A'
può essere qualsiasi cosa; questo significa
che
A può essere scelto in modo tale che la sua divergenza sia una funzione prescelta e il valore del campo magnetico non risentirà di questa scelta.
Quale potenziale vettore dovremo quindi scegliere nelle nostre lezioni? Chiaramente la scelta dovrebbe essere fatta in modo da semplificare al massimo la matematica e quindi dipenderà dal problema di cui ci stiamo occupando.
Scegliere la divergenza del potenziale vettore in generale si dice tecnicamente "SCEGLIERE IL GAUGE".
___________________
Un esempio, il potenziale vettore di un filo infinitamente lungo
Abbiamo dimostrato nella lezione 12c che il campo magnetico di un filo rettilineo infinitamente lungo visto da un osservatore O è
(dove I è chiaramente la corrente che l'osservatore vede)
L'equazione (1) in questo caso si specializza in
la quale esplicitamente si scrive come un sistema di 3 equazioni differenziali
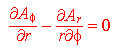
Risulta evidente quasi alla prima occhiata che il sistema ha infinite soluzioni, e trovare quella generica non è proprio elementare; a noi comunque interessa trovarne una particolare. Sapendo che il sistema "filo infinitamente lungo" è caratterizzato da invarianza traslazionale lungo la direzione z e rotazionale attorno a questo stesso asse possiamo imporre lo stesso tipo di simmetria per il campo potenziale. Questo si traduce matematicamente imponendo che tutte le derivate rispetto a z e f siano nulle.
Con questa imposizione si ricava in maniera più che elementare che una soluzione particolare è:
A=[0,0,-2I ln r]
Indice Lezioni - Lezione Precedente - Lezione Seguente