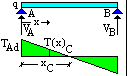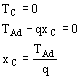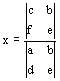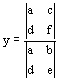Domande frequenti.
© 1999-2002 Carlo PALATELLA
|
||||||||||||
|
Come
si calcola la posizione del punto di annullamento del diagramma del taglio quando il
carico è uniforme? Com'è rivolta la concavità del diagramma parabolico del momento quando il carico è uniforme? Perché occorre ribaltare verticalmente il diagramma dei momenti nel caricare la trave ausiliaria? Come si può impostare un foglio di calcolo per la risoluzione dei sistemi di equazioni lineari? E' più conveniente una trave continua o una serie di travi isostatiche accostate? E' più conveniente una trave semplicemente appoggiata o una trave incastrata agli estremi?
|
||||||||||||
| Come si calcola la posizione del punto di annullamento del diagramma del taglio quando il carico è uniforme? | ||||||||||||
|
|
La variazione del taglio è lineare. Nel punto C di annullamento si ha:
In pratica, la distanza di annullamento è data dal rapporto tra il valore iniziale del taglio (ossia del valore del taglio a partire dal quale comincia la discesa del diagramma) e il carico uniforme q. La formula vale solo nel caso di carico uniforme. |
|||||||||||
| Com'è rivolta la concavità del diagramma parabolico del momento quando il carico è uniforme? | ||||||||||||
|
La concavità della parabola y = ax2
+ bx + c dipende dal segno del coefficiente a. Se a è positivo la concavità è rivolta verso l'asse positivo y; se a è negativo essa è rivolta dalla parte opposta. Ovviamente, a non può essere nullo perché, altrimenti, y sarebbe una retta e non una parabola. Nel caso del diagramma dei momenti l'asse positivo M è rivolto verso il basso: di conseguenza la concavità è rivolta verso il basso se il coefficiente di x2 è positivo. L'espressione di M(x) nell'esempio in figura risulta:
Com'è evidente, il coefficiente di x2 è negativo e quindi la concavità risulta rivolta verso l'alto, verso negativo dell'asse M. |
|||||||||||
| Perché occorre ribaltare verticalmente il diagramma dei momenti nel caricare la trave ausiliaria? | ||||||||||||
|
|
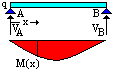
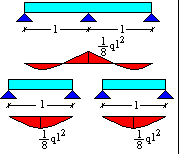
Il diagramma dei momenti è
tracciato, in maniera inusuale, con l'asse positivo rivolto verso il basso, al contrario
di quanto avviene per i diagrammi del taglio e dello sforzo normale. Ribaltare il diagramma verticalmente significa utilizzare l'orientamento verso l'alto dell'asse di riferimento M. La scelta di un asse orientato verso il basso è motivata dal fatto che la disposizione delle armature delle strutture in c.a. è più facile da individuare: è infatti sufficiente che esse seguano fedelmente l'andamento del diagramma dei momenti. |
|||||||||||
| Come si può impostare un foglio di calcolo per la risoluzione dei sistemi di equazioni lineari? | ||||||||||||
|
La soluzione di un sistema di due equazioni in due incognite mediante la regola di Cramer. |
Primo metodo: la regola di
Leibniz - Cramer Il valore della singola incognita è dato dal rapporto tra due determinanti: al denominatore il determinante dei termini noti e al numeratore un secondo determinante, ricavato dal primo mediante la sostituzione della colonna dei coefficienti relativi all'incognita con quella dei termini noti. Nel caso di determinanti del secondo ordine, ossia di determinanti formati da due righe e da due colonne, per il loro calcolo si applica la regola del prodotto in croce. Per determinanti di ordine superiore l'operazione è di gran lunga più complessa. A questo scopo può risultare utile il ricorso a un foglio elettronico. Con MS Excel si procede nel seguente modo:
|
|||||||||||
|
Il sistema
è scritto nella forma matriciale
ed ha per soluzione
|
Secondo metodo:
uso dell'algebra matriciale Si scrive il sistema in forma matriciale uguagliando il prodotto della matrice dei coefficienti e per il vettore delle incognite al vettore dei termini noti. Si costruisce la matrice inversa di quella dei coefficienti e la si moltiplica per il vettore dei termini noti, ricavando in tal modo le incognite. Con MS Excel l'applicazione del metodo è estremamente rapida. In pratica:
Nella pagina sull'uso del foglio elettronico è possibile scaricare degli esempi relativi ai due metodi.
|
|||||||||||
| Nel confronto tra il metodo degli abbassamenti e quello delle rotazioni, quale di essi risulta più conveniente per la risoluzione delle travi iperstatiche? | ||||||||||||
| Per utilizzare il metodo degli abbassamenti occorre costruire il diagramma dei momenti della trave ausiliaria mentre, per il metodo delle rotazioni, è sufficiente il solo calcolo delle reazioni della stessa trave. Ne consegue che il metodo delle rotazioni è di gran lunga più semplice; esso si può, inoltre, avvalere della formulistica relativa alle reazioni A* e B* che è molto più ricca di quella esistente per gli abbassamenti. | ||||||||||||
| E' più conveniente una trave continua o una serie di travi isostatiche accostate? | ||||||||||||
Il momento della trave continua a due campate, in valore assoluto, coincide con quello della trave semplicemente appoggiata. |
n°
campate 2 3 4 5 6 7 |
K +0,125 -0,125 -0,100 -0,107 -0,105 -0,106 -0,106 |
Una trave semplicemente appoggiata
assoggettata ad un carico uniforme q ha un momento massimo positivo pari a
Una trave a due campate di uguale luce ha un momento massimo negativo pari ancora a 0,125 ql2. Nel confronto non si verifica, pertanto, una particolare convenienza in favore della trave continua. Aumentando il numero di campate, sempre con luce costante, il momento massimo è negativo e, a partire dalle sei campate, si attesta su un valore pari a 0,106 ql2. Si può dedurre che la trave continua è più conveniente di quella appoggiata se il numero di campate è maggiore o uguale a tre. Un numero eccessivo di campate non comporta un aumento della convenienza ed è sconsigliato a causa di problemi di deformabilità termica che caratterizzano corpi di fabbrica troppo estesi. |
|||||||||
| Il momento massimo M=Kql2 è minore nella trave continua a partire da tre campate. | ||||||||||||
| E' più conveniente una trave semplicemente appoggiata o una trave incastrata agli estremi? | ||||||||||||
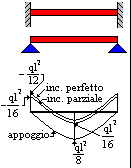 |
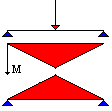
Il momento massimo negativo della trave incastrata assoggettata ad un carico uniforme è pari a
esso risulta uguale ai due terzi di quello della trave appoggiata. Se l'incastro non è perfetto la convenienza può risultare maggiore: più in particolare, con un'efficienza dell'incastro del 67% il momento è il minimo possibile e vale
ovvero metà del valore della trave semplicemente appoggiata. |
|||||||||||