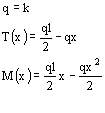Diagrammi sollecitazioni e deformazioni

Relazioni tra q, T, M, j, h
Sollecitazioni		Il carico q, lo sforzo di taglio T, il momento M, le rotazioni delle sezioni j e gli spostamenti h della linea elastica della trave sono legati per mezzo di relazioni differenziali ed integrali. Il taglio è l'integrale del carico, il momento è l'integrale del taglio, le rotazioni sono l'integrale del momento (diviso EI) e gli spostamenti sono l'integrale delle rotazioni. E è il modulo di elasticità del materiale, I è il momento di inerzia baricentrico della sezione.


Deformazioni


Le relazioni tra carico, sollecitazioni e deformazioni.
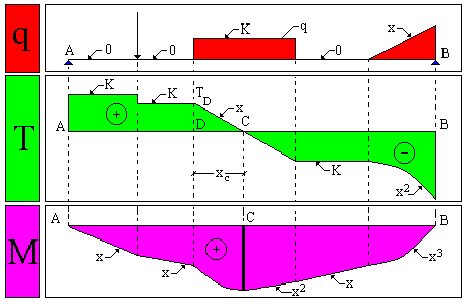
Ciò consente di riconoscere facilmente l'andamento dei diagrammi delle sollecitazioni e delle deformazioni, in relazione al tipo di carico applicato sul singolo tratto omogeneo di trave. Ad esempio, se il carico è costante, il taglio avrà una variazione lineare, il momento varierà con x², le rotazioni con x³ e gli spostamenti, infine, con x⁴.

zero	costante	x	x²	x³	x⁴	x⁵	x⁶
q	T	M	j	h
	q	T	M	j	h
		q	T	M	j	h
			q	T	M	j	h

Il massimo (e il minimo) del momento si verificano nei punti in cui il taglio è nullo: la condizione per il verificarsi del massimo (e del minino) della funzione momento è, infatti, che sia nulla la sua derivata prima, il taglio per l'appunto.

Il sostanziale parallelismo tra la relazione che lega il carico q e il taglio T da una parte e la rotazione j e i momento M dall'altra consente di ricavare le deformazioni mediante il tracciamento dei diagrammi di una trave, la trave ausiliaria, caricata con il diagramma dei momenti (teorema e corollari di Mohr).

Le funzioni delle sollecitazioni e delle deformazioni per la trave semplicemente appoggiata, caricata con carico distribuito uniforme.

T = 0:

momento minimo (punti A e B) momento massimo (punto C con)

Taglio positivo: momento crescente: tratto AC

Taglio negativo: momento decrescente: tratto CB