A.G.a.Fe
(Algebraic Geometry at Ferrara)
Le Origini
Integrali del tipo
(1)
dove p(x)
e P(x) sono polinomi e P(x) di grado maggiore o uguale a due,
interessarono analisti e geometri già a partire dall’ultimo ventennio del XVII
secolo. Questi integrali si presentarono nello studio di problemi di meccanica
e nella determinazione della lunghezza di archi di curve piane. Questi ultimi
per lungo tempo furono chiamate “quadrature”.
Ad esempio l’integrale:
definisce la lunghezza dell’arco della circonferenza x2 +y2 =1 nel
primo quadrante. Il caso in cui il polinomio P(x) ha grado 2 non presenta difficoltà. Infatti, se P(x)=ax2+bx+c la curva piana di
equazione y=ax2+bx+c
ammette una parametrizzazione
x=φ (t)
y=ψ(t)
con φ e ψ funzioni razionali
del parametro t e l’integrale I è riconducibile all’integrazione di
funzioni razionali. Diverso è il caso in cui il grado di P(x) degP(x), è uguale o maggiore di 3, come nel caso dell’area dell’ellisse:
.
In quest’ultimo
caso, la lunghezza dell’arco è data da:
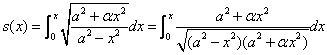(2)
ove
.
Agli integrali (1),
quando 
, dedicarono parte delle loro ricerche eminenti
matematici del XVII secolo, tra questi Jakob Bernoulli (1667–1748), che studiò gli integrali
legati alla lunghezza dell’arco di iperbole e della spirale logaritmica,
ed il fratello Johann Bernoulli (1654–1705) che considerò il caso della
parabola cubica. Nel 1694, nel corso dei suoi studi di meccanica, Jakob Bernoulli fu condotto a studiare
l’integrale
che rappresenta la
lunghezza di un arco della curva di equazione:
,
detta lemniscata di Bernoulli o
semplicemente lemniscata [Curvatura Laminae
elasticae, Acta Eruditorum 13, 207–276, (1694)]. Questo integrale avrà un
ruolo fondamentale nello sviluppo della teoria delle nuove funzioni
trascendenti.
Il fratello Johann Bernoulli, dopo essere
riuscito ad integrare alcune funzioni razionali, asserì nella memoria Problema Exhibitum
a Jo. Bernoullo [Acta Eruditorum del 1703,
pp. 26–31] che l’integrale di ogni funzione razionale non contiene funzioni
trascendenti diverse dal logaritmo e dalle funzioni trigonometriche. Poiché il
denominatore di una funzione razionale è un polinomio di grado n in x,
la correttezza dell’asserzione dipendeva dal fatto che ogni polinomio a coefficienti
reali potesse essere espresso come prodotto di fattori di primo e di secondo
grado a coefficienti reali.
La classe di integrali
per cui P(x) ha grado maggiore o uguale a 3 e radici tutte distinte, pose
seri ostacoli alla congettura, in voga in quei tempi, secondo la quale, ogni
integrale di quel tipo sarebbe stato esprimibile in termini delle sole funzioni
elementari (funzioni razionali, trigonometriche, esponenziale e loro inverse)
attraverso un numero finito di operazioni algebriche.
Quando ogni sforzo per
ridurre gli integrali sopra detti a quelli noti fallì, nella mente dei
matematici incominciò a farsi strada l’idea che questi integrali dessero luogo
a nuove funzioni trascendenti (in effetti ciò fu provato soltanto nel 1833 da Joseph Liouville (1809–1882) in Mémoire sur le trascendantes elliptiques de premiére et de
seconde espéce considérées comme fonctions de leur amplitude [J. École
Polytecnique 23, 1834, pp. 37–83]).
Si seguirono due
indirizzi di ricerca:
• Da una parte si cercò
di risolvere tali integrali, introducendo il minor numero possibile di nuove
funzioni trascendenti,
• Dall’altra si cercò
quali fossero le proprietà intrinseche alle nuove trascendenti.
Molti furono i
ricercatori che, senza raggiungere risultati importanti, seguirono la prima
linea. Tra questi citiamo:
Colin Mac Laurin (1698–1746), in A treatise
of Fluxions (1742) ; Vincenzo
Riccati (1707–1775), in Opuscola
(1742) ; Jean-Baptiste Le Rond
D’Alembert (1717–1783), in Mémoires
de L’Academie des Sciences et belle lettres
(1746, 1748). Anche
Leohnard Euler trattò quest’argomento in vari lavori pubblicati in Acta Academiae Scientiarum imperialis Petropolitanae. Essi
provarono a ridurre quanti più integrali del tipo sopra detto all’integrale
rappresentante la lunghezza dell’arco dell’ellisse che erroneamente era
considerato il più semplice. A ragione di ciò, gli integrali del tipo (1) per
cui deg(P(x))≥3 furono chiamati “integrali ellittici”.
L’integrale (2) fu considerato per la prima volta nel 1665 da John Wallis
(1616–1703) in Arithmetica
infinitorum. Egli considerò anche la
lunghezza dell’arco di varie cicloidi e confrontò la lunghezza di questi archi
con quella dell’ellisse. Questo linea di ricerca si concluse con l’opera di Adrien-Marie Legendre
che introdusse la forma trigonometrica per gli integrali ellittici e ne
eseguì una classificazione (vedi oltre).
La seconda via, ossia
studiare le proprietà intrinseche di queste funzioni, fu alquanto più dura, specialmente
a causa della limitazione dell’analisi al campo reale, ossia senza l’uso della
variabile complessa. Tuttavia un fatto attrasse presto l’attenzione di alcuni
matematici, fatto che avrebbe dovuto indicare la direzione d’attacco del
problema. Erano note le equazioni differenziali a variabili separate del tipo:
f(x)dx=±f(y)dy
per le quali, benché
non esistano integrali algebrici dei singoli membri, l’equazione differenziale
ha un integrale algebrico. Questo era ad esempio il caso in cui una primitiva
di f(x) è una funzione logaritmo o una funzione trigonometrica inversa.
Fu Johann Bernoulli che per
primo si domandò se queste proprietà non potessero valere per altre funzioni
trascendenti diverse dai logaritmi o dalle funzioni trigonometriche inverse.
Nel 1698, egli aveva anche scoperto che la differenza di due archi della
parabola cubica (y=x3) è
integrabile [Theorema
universale rectificazioni lineaurum
curvarum inferviens: Nova parabolarum proprietas. Cubicalis primaria arcum menfura, Acta Eruditorum, Ottobre 1698], risultato che
aveva ottenuto casualmente e che giudicava molto elegante. La prima risposta
alla questione posta da Bernoulli contenente un
risultato veramente interessante fu data da Giulio
Carlo de’ Toschi conte di Fagnano.
|
precedente |