A.G.a.Fe (Algebraic Geometry at Ferrara)

 

Legendre e la riduzione alle forme canoniche

 

 

 

La forma più generale degli integrali ellittici venne introdotta nel 1784 da G. Lagrange nella memoria Sur un nouvelle méthode de calcul intégral ect. [Mémoire de l’Academie Reale des Sciences de Turin, II, 1784–1785, Oeuvres, 2, pp. 253–312]. Essi sono della forma :

ove P(x, y) è una funzione razionale e  y2  = a0 x4 + 4a1 x3+ 6a2 x2 + 4a3 x + a4  è un polinomio a radici distinte (senza escludere la possibilità che sia a0 = 0, nel qual caso  ). In questa memoria, Lagrange, espone dei metodi di calcolo numerico per tali integrali. Egli inizia mostrando come essi possano sempre essere ridotti ad una somma di espressioni elementari e di un integrale del tipo:

dove N(x) è una funzione razionale di x2, p, q reali con p > q.

 

Questi erano i principali risultati nel campo degli integrali ellittici al tempo in cui iniziò ad occuparsene Adrien-Marie Legendre. I suoi primi studi sugli integrali ellittici risalgono al 1786, anno in cui egli presentò all’Accademia delle Scienze di Parigi la Mémoire sur l’intégration par arcs d’ellipse et sur la comparation de ces arcs. La memoria più importante sull’argomento delle funzioni trascendenti è però la Mémoire sur les trascendantes elliptiques che presentò all’Accademia delle Scienze di Parigi nel 1973. In questa memoria, Legendre, si propone di confrontare tra loro tutte le trascendenti ellittiche, di classificarle in differenti specie, riducendole alla forma più semplice possibile e di determinare il metodo più facile e rapido per il loro calcolo approssimato. Il risultato principale di questa memoria è la classificazione di tutti gli integrali ellittici in tre tipi, classificazione che, dopo gli Exercices de calcul intégral [Vol. I, 1811] , si può enunciare:

Ogni integrale ellittico è sempre riconducibile all’integrale di una funzione razionale, più la somma di integrali dei seguenti tre tipi:

ove

Gli Exercises, pubblicati in tre volumi tra il 1811 e il 1817, furono perfezionati nella sua opera maggiore: Traité des fonction élliptiques et des integrales eulériennes,  avec des tables pour en faciliter le calcul numerique, in tre volumi stampati tra il 1825 e il 1828. L’uso dell’espressione “fonctions elliptiques” da parte di Legendre nel titolo del trattato può dar luogo a qualche confusione. Poiché gli integrali sono funzioni del secondo estremo di integrazione, Legendre chiamò questi integrali “funzioni ellittiche”; oggi, come ben noto, si riserva questo nome alle funzioni meromorfe doppiamente periodiche, tra le quali vi sono le funzioni che si ottengono invertendo gli integrali ellittici di prima specie (v. Abel).

Nell’ “avertissement”  del Traité [vol. I], si legge:

 

La partie la plus étendue et en même temps la plus importante de l’ouvrage que l’Auteur a publié sous le nome d’Exercises de calcul intégral, est, comme on sait, qui traite des fonctions elliptiques, et leur application à différens problémes de Géométrie et de Mécanique, celle, et de la construction des tables nécessaires pour l’usage de ces fonctions. Cette partie, ainsi que celle qui concerne le intégrales

définies, auxquelles l’Auteur a donné le nom d’intégrales Eulériennes, sont reproduites dans ce nouveau Traité avec un grand nombre d’additions dont l’objet est de perfectionner la théorie de ces trascendantes...

 

La parte più estesa e allo stesso tempo più importante dell’opera che l’autore ha pubblicato sotto il nome di Esercizi di calcolo integrale, è, come si sa, quella che tratta delle funzioni ellittiche, e loro applicazioni a differenti problemi di geometria e meccanica, e della costruzione di tavole necessarie per l’uso di queste funzioni. Questa parte, così come quella che concerne gli integrali definiti, ai quali l’autore ha dato il nome di integrali Euleriani, sono riprodotte in questo trattato con un gran numero di aggiunzioni, il cui scopo è quello di perfezionare la teoria di queste trascedenti...

 

E più avanti:

 

Il ne sera pas inutile pour l’histoire de la Sciences, de faire remarquer ici que cette nouvelle branche d’analyse à laquelle l’Auteur a donné le nom de Théorie des fonctions elliptiques, est fondée en grande partie sur les bases établies dans le chap. V, concernant la forme la plus simple de ces fonctions et leur division en troi espéces...

 

Non sarà difficile per la storia della Scienza, fare osservare qui che questa nuova branca dell’analisi alla quale l’Autore ha dato il nome di Teoria delle funzioni ellittiche, è fondata in gran parte sulle basi stabilite nel capitolo V, concernente la forma più semplice di queste funzioni e loro divisione in tre specie...

 

Ricordiamo che la forma “trigonometrica” dei tre tipi fondamentali, fu introdotta da Legendre nel primo volume degli Exercises, ma la prima riduzione fu effettuata alle forme seguenti:

 

 

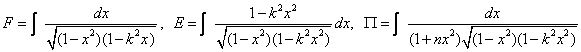
equivalenti alle precedenti posto x=sinФ.

Legendre introdusse anche la nomenclatura che diverrà poi d’uso comune. Egli chiama: Ф amplitudine, k modulo, modulo complementare e n = c-2  parametro della funzione ellittica.

Legendre nei primi due volumi del Traité:

Il terzo volume del 1828, dedicato alle funzioni euleriane, consta anche di tre supplementi, datati il 12 Agosto 1828, il 15 Marzo 1829 e il 4 Marzo 1832, destinati a completare il suo trattato con le scoperte di Abel e Jacobi.

Nell’introduzione al primo supplemento, Legendre scrisse:

 

Aprés m’être occupé pendant un grand nombre d’années de la théorie des fonctions elliptiques, dont l’immortel Euler avait posé les fondamens, j’ai cru devoir rassembler les résultats de ce long travail dans un Traité qui a été rendu public de Janvier 1827. Jusque là les géométres n’avaient pris presque aucune part à ce genre de recherches; mais à peine mon ouvrage avait-il vu le jour , à peine son titre pouvait-il être connu des savants étranger, que j’appris, avec autant d’étonnement que de satisfation que deux jeunes géomètres, M.M Jacobi de Könisberg et Abel de Christiania, avaint réussi, par leur travaux particuliers, à perfectionner considéreblement la théorie des fonctions elliptiques dans ses les plus élevés.

 

Prima di essermi occupato, per un gran numero di anni, della teoria delle funzioni ellittiche di cui l’immortale Euler aveva posto le fondamenta, ho pensato di dover riunire i risultati di questo lungo lavoro in un trattato che è stato reso pubblico nel Gennaio 1827. Fino a quel momento i geometri non avevano preso parte a questo genere di ricerche; ma non appena la mia opera ha visto la luce, non appena il suo titolo fu conosciuto dai dotti stranieri, ho appreso con tanto stupore, quanta soddisfazione, che due giovani geometri, i signori Jacobi di Könisberg e Abel di Christiana, erano riusciti, attraverso i loro particolari lavori, a perfezionare considerevolmente la teoria delle funzioni ellittiche nei suoi più alti gradi.

 

I primi due supplementi, sono dedicati principalmente all’opera di Jacobi. Il terzo supplemento tratta principalmente delle scoperte di Abel e del suo famoso teorema di addizione (versione “iperellittica”). Legendre (nell’Avertissement al III libro) informa che la prima memoria di Abel, stampata nel numero 12, nel secondo volume del giornale di Crelle [Journal für die reine und angewandte mathematik], costituisce già una teoria quasi completa delle funzioni ellittiche. Legendre concluse la sua opera con le seguenti parole:

 

Nous terminerons ici les additions que nous nous étions proposé de faire à notre ouvrage, en profitant des découvertes récentes de MM. Abel et Jacobi dans la théorie des fonctions elliptiques. On remarquera que la plus importante de ces additions consiste dans la nouvelle branche d’analyse que nous avons déduite du théoréme de M. Abel, et qui était restée jusqu’ici tout-à-fait inconnue aux géométres. Cette branche d’analyse, à laquelle nous avons donné le nom de théorie des fonctions ultra-elliptiques, est infiniment plus étendue que celle des fonctions elliptiques, avec laquelle elle a des rapports trés intimes; elle se composes d’un nombre indéfini de classes, qui se divisent chacune en trois espéces comme les fonctions elliptiques, et qui ont d’ailleurs un grand nombre de propriétés. Nous n’avons pu qu’effleurer cette matiére; mais on peut croire qu’elle s’enrichira progressivement par les travaux des géométres, et qu’elle finira par former une des plus belles parties de l’analyse des trascendantes.

 

Noi termineremo qui i complementi che ci siamo proposti di fare alla nostra opera, approfittando delle recenti scoperte di MM. Abel e Jacobi sulla teoria delle funzioni ellittiche. Si sottolineerà che la più importante di queste aggiunte consiste nella nuova branca dell’analisi che abbiamo dedotto dal teorema di M. Abel, e che è rimasto fino ad ora sconosciuto ai geometri. Questa branca dell’analisi, alla quale noi abbiamo dato il nome di teoria delle funzioni ultra-ellittiche è infinitamente più estesa di quella delle funzioni ellittiche, con la quale essa ha dei rapporti molto stretti; essa si compone di un numero indefinito di classi, che si dividono ciascuna in tre specie, come le funzioni ellittiche, e qui abbiamo d’altronde un gran numero di proprietà. Noi non abbiamo potuto che sfiorare questa materia; ma si può credere che essa si arrichirà progressivamente per i lavori dei geometri, e che essa finirà per formare una delle più belle parti dell’analisi delle trascendenti.

 

Nelle sue ricerche di sugli integrali ellittici, Legendre, ottenne molti risultati che non erano stati enunciati nelle opere dei suoi predecessori ed organizzò, mediante la classificazione in tipi delle nuove trascendenti, questo ramo della matematica; tuttavia egli, non vi apportò nessuna nuova idea importante, nè sfiorò il nuovo approccio di Abel e di Jacobi. Quando Legendre venne a conoscenza delle ricerche di Abel e Jacobi le elogiò grandemente, con molta umiltà. Legendre aveva sfiorato, senza accorgersene, la possibilità di fare una delle più grandi scoperte matematiche della sua epoca.

 

 

precedente

home

successivo